线性结构应用-栈与队列
栈
一、栈的定义
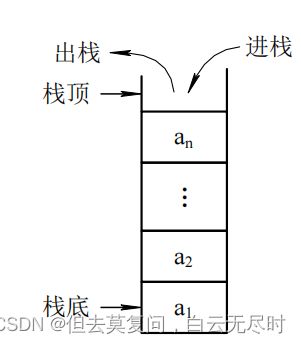
栈作为一种限定性线性表, 是将线性表的插入和删除运算限制为仅在表的一端进行 ,通常将允许进行插入、删除操作的一端称为 栈顶(Top),另一端称为 栈底 (Bottom) 。不含任何元素的栈称为 空栈 。栈是一种 后进先出 (Last In First Out) 的线性表,简称为 LIFO 表。
很多类似的软件,比如Word、Photoshop等文档或图像编辑软件中,都有撤销(undo)的操作,也是用栈这种方式来实现的,当然不同的软件具体实现代码会有很大差异,不过原理其实都是一样的。
二、栈的存储结构
顺序结构
#define MAXSIZE //<最大元素数>
typedef struct
{
datatype elem[MAXSIZE];
int top; //用于栈顶指针
} SeqStack为什么栈顶指针不是int*类型?
栈顶指针不是int *类型是因为栈顶指针实际上是一个索引值,指向栈顶元素在数组中的位置。使用int类型可以更方便地进行索引操作,而不需要进行指针的复杂操作。另外,栈顶指针的值通常是一个整数,表示距离栈底的偏移量,因此int类型更符合实际的使用需求。
链式结构
三、基本操作
(1) 栈初始化 Init_Stack(S):构造了一个空栈。
void Init_Stack(SeqStack *S)
{
S->top=-1;
}(2) 入栈 Push_Stack(S, x):栈 S 已存在且不满,在栈 S 的顶部插入一个新元素 x,x 成为新的栈顶元素。栈发生变化。、
int Push_SeqStack(SeqStack *S, datatype x) /*插入数据元素 x */
{
if(S->top==MAXSIZE-1) /*栈满不能入栈*/
return 0;
else
{
S->top++; /*栈顶指针加 1 */
S->elem[S->top]=x; /*将插入数据元素 x 赋给栈顶空间*/
return 1;
}
}(3) 出栈 Pop_Stack(S):栈 S 存在且非空。将栈 S 的顶部元素从栈中删除,栈中少了一个元素。栈发生变化。
int Pop_SeqStack(SeqStack *S, datatype *x)
{
if(S->top==-1)
return 0; /*栈空不能出栈*/
else
{
*x=S->elem[S->top]; /*栈顶元素存入*x,返回*/
S->top--; /*栈顶指针减 1 */
return 1;
}
}(4) 读栈顶元素 Top_Stack(S):栈 S 存在且非空。栈顶元素作为结果返回,栈不变化。
int GetTop(SeqStack S,datatype *x)
{
if(S->top==-1)
return;
else
{
*x=S->elem[S->top];
return 1;
}
}四、栈应用与递归
递归是指在定义自身的同 时又出现了对自身的调用。如果一个函数在其定义体内直接调用自己,则称其为直接递归函数。如果一个函数经过一系列的中间调用语句,通过其他函数间接调用自己,则称其为间接递归函数。
汉诺塔
队列
一、队列的定义
队列是一种操作受限的线性表,在表中只允许进行插入的一端称为 队尾 (rear) ,只允许进行删除的一端称为 队头 (front) 。队列的插入操作通常称为入队列或进队列,而队列的删除操作则称为出队列或退队列。当队列中无数据元素时,称为 空队列 。这种表是按照 先进先出 (FIFO , first in first out) 的原则。
二、队列的存储结构
typedef struct node
{
datatype data;
struct node *next;
} QNode; /*链队结点的类型*/
typedef struct
{
QNnode *front, *rear;
} LQueue;三、基本操作
(1) 队列初始化 Init_Queue(q):
队列 q 不存在,构造了一个空队。
int Init_LQueue(LQueue *q)
{
if((q->front=(QNode *)malloc(sizeof(QNode)))==NULL) /*申请头、尾指针结点*/
return 0;
q->rear=q->front;
q->front->next=NULL;
return 1;
}(2) 入队操作 In_Queue(q, x):
队列 q 存在,对已存在的队列 q,插入一个元素 x 到队尾,队发生变化。
int In_LQueue(LQueue *q, datatype x)
{
QNode *p;
if((p=(QNode *)malloc(sizeof(QNode)))==NULL) /*申请新结点*/
return 0;
p->data=x;
p->next=NULL;
q->rear->next=p;
q->rear=p;
return 1;
}(3) 出队操作 Out_Queue(q, x):
队列 q 存在且非空,删除队首元素,并返回其值,队发生变化。
int Out_LQueue(LQueue *q, datatype *x)
{
QNode *p;
if(Empty_LQueue(q))
{
printf(″队空″);
return 0;
} /*队空,出队失败*/
else
{
p=q->front->next;
q->front->next=p->next;
*x=p->data; /*队头元素放 x 中*/
free(p);
if(q->front->next==NULL)
q->rear=q->front; /*只有一个元素时,出队后队空,此时还要修改队尾指针*/
return 1;
}
}(4) 读队头元素 Front_Queue(q, x):
队列 q 存在且非空,读队头元素,并返回其值,队不变。
(5)判断队空
队列如果为空,即队头指针和队尾指针相等,返回 1;否则,返回 0。
int Empty_LQueue(LQueue *q)
{
if(q->front==q->rear)
return 0;
else
return 1;
}四、循环队列
类型定义
#define MAXSIZE 100
typedef struct
{
datatype data[MAXSIZE]; /*队列的存储空间*
int front, rear; /*队头、队尾指针*/
} SeqQueue; /*循环队*/初始化
void InitQueue (SeqQueue * Q)
{/* 将*Q 初始化为一个空的循环队列 */
Q->front=Q->rear=0:
}入队
int EnterQueue(SeqQueue *Q, QueueElementType x)
{ /*将元素x入队*/
if((Q->rear+1)%MAXSIZE==Q->firont)/*队列已经满了*/
return (FALSE);
Q->element[Q->rear]=x,
Q->rear=(Q->rear+1)%MAXSIZE;/*重新设置队尾指针 */
return(TRUE);/*操作成功*/
}
出队
int DeleteQueue(SeqQueue *Q, QueueElementType * x)
{/*删除队列的队头元素,用x返回其值*/
if(Q->front==O->rear) /*队列为空*/
return(FALSE):
*x=Q->element[Q->front];
Q->front=(O->front+1)%MAXSIZE;/*重新设置队头指针*/
return(TRUE); /*操作成功*/
}