【车间调度】基于遗传算法求解车间调度
作业车间调度问题描述
作业车间调度问题(Job Shop Scheduling, JSP)是最经典的几个NP-hard问题之一。其应用领域极其广泛,涉及航母调度,机场飞机调度,港口码头货船调度,汽车加工流水线等。
JSP问题描述:一个加工系统有M台机器,要求加工N个作业,其中,作业i包含工序数为Li。令,则L为任务集的总工序数。其中,各工序的加工时间已确定,并且每个作业必须按照工序的先后顺序加工。调度的任务是安排所有作业的加工调度排序,约束条件被满足的同时,使性能指标得到优化。
作业车间调度需要考虑如下约束:
Cons1:每道工序在指定的机器上加工,且必须在其前一道工序加工完成后才能开始加工;
Cons2:某一时刻1台机器只能加工1个作业;
Cons3:每个作业只能在1台机器上加工1次;
Cons4:各作业的工序顺序和加工时间已知,不随加工排序的改变而改变。
问题实例
下面给出作业车间调度问题的一个实例,其中每个工序上标注有一对数值(m,p),其中,m表示当前工序必须在第m台机器上进行加工,p表示第m台机器加工当前工序所需要的加工时间。(注:机器和作业的编号从0开始)
jop0=[(0,3),(1,2),(2,2)]
jop1=[(0,2),(2,1),(1,4)]
jop2=[(1,4),(2,3)]
在这个例子中,作业jop0有3道工序:它的第1道工序上标注有(0,3),其表示第1道工序必须在第0台机器上进行加工,且需要3个单位的加工时间;它的第2道工序上标注有(1,2),其表示第2道工序必须在第1台机器上进行加工,且需要2个单位的加工时间;余下的同理。总的来说,这个实例中共有8道工序。
该问题的一个可行解是L=8道工序开始时间的一个排列,且满足问题的约束。下图给出了一个可行解(注:该解不是最优解)的示例:![]()
%% 清空环境
clc;clear
%% 下载数据
load scheduleData Jm T JmNumber
%工序 时间
%% 基本参数
NIND=40; %个体数目
MAXGEN=50; %最大遗传代数
GGAP=0.9; %代沟
XOVR=0.8; %交叉率
MUTR=0.6; %变异率
gen=0; %代计数器
%PNumber 工件个数 MNumber 工序个数
[PNumber MNumber]=size(Jm);
trace=zeros(2, MAXGEN); %寻优结果的初始值
WNumber=PNumber*MNumber; %工序总个数
%% 初始化
Number=zeros(1,PNumber); % PNumber 工件个数
for i=1:PNumber
Number(i)=MNumber; %MNumber工序个数
end
% 代码2层,第一层工序,第二层机器
Chrom=zeros(NIND,2*WNumber);
for j=1:NIND
WPNumberTemp=Number;
for i=1:WNumber
%随机产成工序
val=unidrnd(PNumber);
while WPNumberTemp(val)==0
val=unidrnd(PNumber);
end
%第一层代码表示工序
Chrom(j,i)= val;
WPNumberTemp(val)=WPNumberTemp(val)-1;
%第2层代码表示机器
Temp=Jm{val,MNumber-WPNumberTemp(val)};
SizeTemp=length(Temp);
%随机产成工序机器
Chrom(j,i+WNumber)= unidrnd(SizeTemp);
end
end
%计算目标函数值
[PVal ObjV P S]=cal(Chrom,JmNumber,T,Jm);
%% 循环寻找
while gentrace(1,gen)
Val1=PVal;
Val2=P;
MinVal=trace(1,gen);
STemp=S;
end
end
% 当前最佳值
PVal=Val1; %工序时间
P=Val2; %工序
S=STemp; %调度基因含机器基因
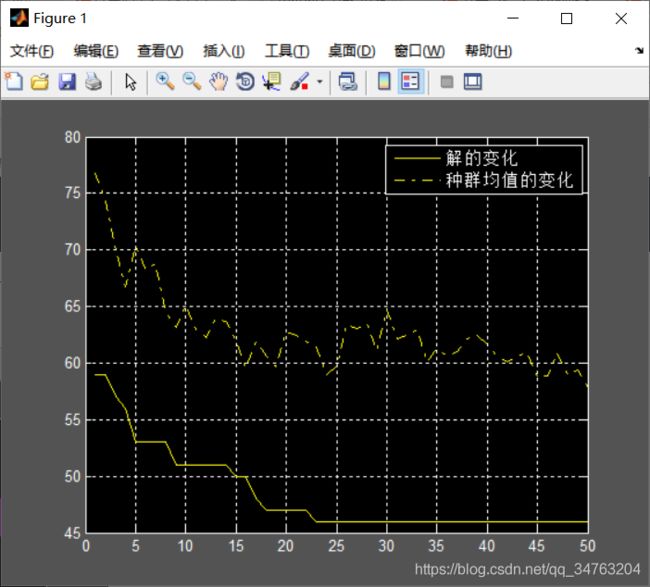
%% 描绘解的变化
figure(1)
plot(trace(1,:));
hold on;
plot(trace(2,:),'-.');grid;
legend('解的变化','种群均值的变化');
%% 显示最优解
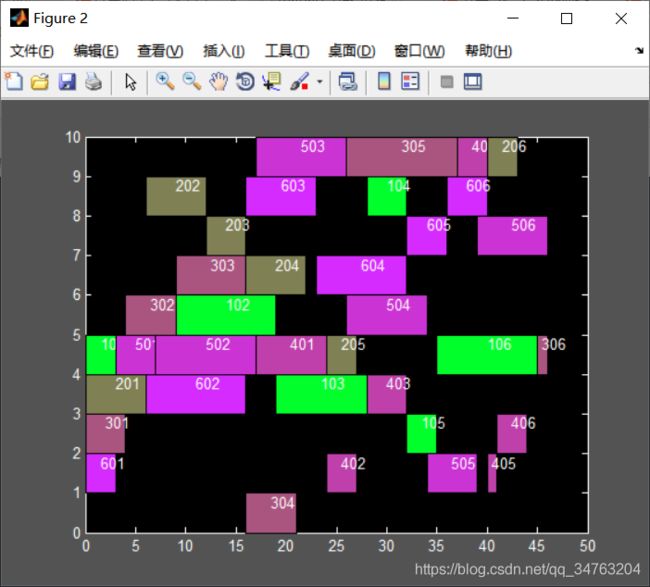
figure(2);
MP=S(1,PNumber*MNumber+1:PNumber*MNumber*2);
for i=1:WNumber
val= P(1,i);
a=(mod(val,100)); %工序
b=((val-a)/100); %工件
Temp=Jm{b,a};
mText=Temp(MP(1,i));
x1=PVal(1,i);
x2=PVal(2,i);
y1=mText-1;
y2=mText;
plotRec(x1,x2,mText);
plotRec(PVal(1,i),PVal(2,i),mText);
hold on;
fill([x1,x2,x2,x1],[y1,y1,y2,y2],[1-1/b,1/b,b/PNumber]);
text((x1+x2)/2,mText-0.25,num2str(P(i)));
end 完整代码添加QQ1575304183