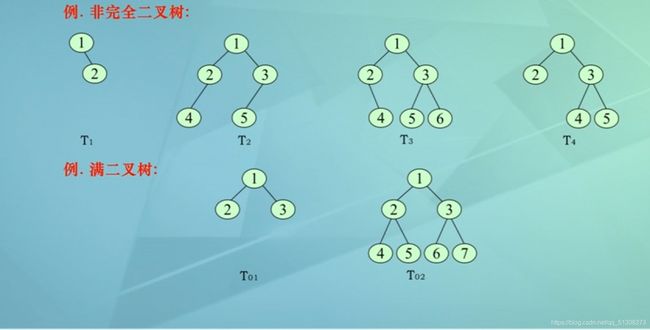
C语言——数据结构之树与二叉树(上)(树的定义,二叉树的定义、存储结构与遍历)
前言
ps:(一点废话)突然发现上一篇更新是3月31号,咕咕
树的内容比较多,这里分成两次发,(下一次不知道是什么时候)
从这里开始,就不再是单纯的线性结构了,在日常生活中,其实两个元素之间有时不仅仅是线性关系,往往有着更复杂的结构,树的应用更为广泛
一、树的定义
1.定义和术语
(1)树(tree)(递归定义):是n(n>=0)个结点的有限集T
当n=0时,T为空树
当n>0时,
①有且仅有一个称为T的根的结点
②当n>1时,余下的结点分为m(m>0)个互不相交的有限集T1,T2,…,Tm,每个Ti(1<=i<=m)也是一棵树,且称为根的子树

如图,A有三颗子树BGI;B有两棵子树CF,依次类推
(2)举例
例1:一个结点的树 T1 = {A}
例2:四个结点的树,A为根,BCD为A的子树,则
T2={A,B,C,D}
T21={B}
T22={C}
T23={D}
2.与结点相关的名称
(1)结点的度(degree):结点的子树数目
(2)树的度:树中各结点的度的最大值
(3)n度树:度为n的树
(4)叶子(终端结点):度为0的结点
(5)分枝结点(非终端结点,非叶子):度不为0的结点
(6)双亲(父母,parent)和孩子(儿子,child):若结点C是结点p的子树的根,称P是C的双亲,C是P的孩子
注:一个结点的孩子可以有多个,但孩子的双亲结点只有一个

如图,A的度为3,C的度为4,且C是所有结点中度最大的结点,故此树的度为4。
BHDEFG都是叶子结点,AC为分枝结点。
A是BCH的双亲,BCH是A的孩子
(7)结点的层(level):规定树T的根的层为1,其余任一结点的层等于其双亲的层加一
(8)树的深度(depth,高度):树中各结点的层的最大值
(9)兄弟(sibling):同一双亲的结点之间互为兄弟
(10)堂兄弟:同一层号的结点互为堂兄弟
树的深度为3,DEFG之间互为兄弟,GI之间互为堂兄弟
各结点之间的关系可能是双亲与孩子,互为兄弟、堂兄弟,除此之外,还有祖先与子孙关系
(11)祖先:从树根到某结点所经分枝上的所有结点为该结点的祖先
如图,F的祖先结点为AC
(12)子孙:一个结点的所有子树的结点为该结点的子孙
3.有序树与无序树
(1)有序树:若任一结点的各棵子树,规定从左至右是有次序的,即不能互换位置,则称该树为有序树
(2)无序树:若任一结点的各棵子树,规定从左至右是无次序的,即能互换位置,则称该树为无序树
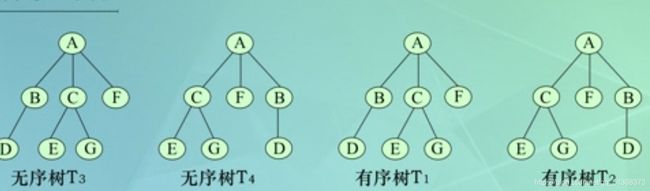
所以T3与T4是两棵相同的树,而T1与T2是两棵不同的树
4.森林
森林F={T1,T2,T3}
(2)任何一棵非空树可表示为一个二元组Tree=(root,F)
其中,root为根结点,F被称为子树森林

5.树的操作
分为三类:查找类、插入类、删除类
(1)查找类
①Root(T):求树的根结点
②Value(T,cur_e):求当前结点的元素值
③Parent(T,cur_e):求当前结点的双亲结点
④LeftChild(T,cur_e):求当前结点的最左孩子
⑤RightSibling(T,cur_e):求当前结点的最右兄弟
⑥TreeEmpty(T):判断树是否为空
⑦TreeDepth(T):求树的深度
⑧TraverseTree(T,Visit()):遍历
其中,遍历操作需按照某种规则访问树的每一个结点,是其他运算的基础
(2)插入类
①InitTree(&T):初始化置空树
②CreateTree(&T,definition):按定义构造树
③Assign(T,cur_e,value):给当前结点赋值
④InsertChild(&T,&p,i,c):将以c为根的树插入为结点p的第i棵子树
(3)删除类
①ClearTree(&T):将树清空
②DestroyTree(%T):销毁树的结构
③DeleteChild(&T,&p,i):删除结点p的第i棵子树
6.树结构的特点
线性结构 ------------------------------------------------ 树型结构
第一个数据元素(无前驱) 根结点(无前驱)
最后一个数据元素(无后继) 多个叶子结点(无后继)
其他数据元素(一个前驱、一个后继) 其他数据元素(一个前驱、多个后继)
正是由于这种特征,使得树的操作比线性结构要复杂的多
二、二叉树的定义与性质
1.定义和术语
(1)二叉树的递归定义
二叉树是n个结点的有限集,可分为两种情形
①如果n=0.为一颗空的二叉树
②如果n>0,则它包含一个根节点,而剩下的结点分为两个不想交的子集,分别构成根节点的左子树与右子树
(2)特点:
①每个结点至多有两棵子树(即不存在度大于2的结点)
②二叉树的子树有左右之分,且其次序不能任意颠倒
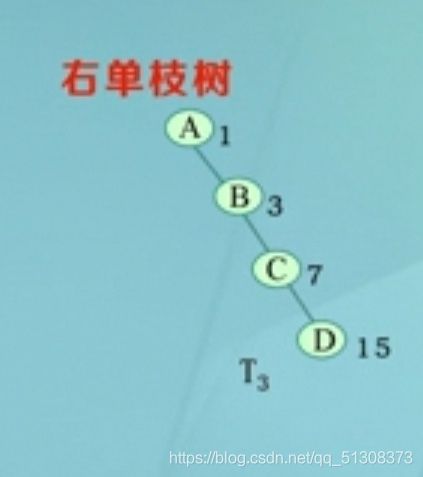
T3中根节点A:左子树为空,右子树为B
结点B:仅有左子树
2.二叉树的操作
(1)二叉树的基本操作
①置T为空二叉树
②销毁二叉树
③生成二叉树:生成哈夫曼树、二叉排序树、平衡二叉树、堆
④遍历二叉树:按某种规则访问T的每一个结点一次且仅一次的过程
⑤求结点的层号
⑥求结点的度
⑦求二叉树的深度
⑧插入/删除一个结点
⑨求二叉树的叶子/非叶子
等等
看似有些复杂,其实我们将它分为三类:查找类、插入类、删除类
(2)查找类
查找类的基础操作在上述树的基本操作中已经给出,其中我们要重点关注的是二叉树的遍历
分为:
①先序遍历:PreOrderTraverse(T,Visit())
②中序遍历:InOrderTraverse(T,Visit())
③后序遍历:PostOrderTraverse(T,Visit())
④层序遍历:LevelOrderTraverse(T,Visit())
(3)插入类
大体同树的基本操作
(4)删除类
大体同树的基本操作
3.二叉树的性质和特殊二叉树
(1)性质1.在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
证明:用归纳法
①当i=1,即第一层只有一个根节点,显然成立
②假设对所有的j(1<=j
由归纳假设:
第i-1层上至多有2^(i-2)个结点,又由于二叉树每个结点的度最大为2,所以第i上结点总数最多为第i-1层最大结点数的2倍。
即:2*2^(i-2) =2 ^(i-1)
(2)性质2.深度为k的二叉树至多有2^k-1个结点(可由性质1推导而来)
(3)性质3.二叉树中,终端结点数n0;度为2的结点数n2。
二者关系:n0=n2+1
证明:
①设二叉树中度为i的结点数为ni,则结点总数n=n0+n1+n2
②除根节点外,每个结点都是另一结点的孩子,孩子数=n-1
③度为i(i=0,1,2)的结点,有i个孩子,则孩子数=2n2+n1
④即可得出n-1=2n2+n1,又已知n=n0+n1+n2。
⑤二式联立,可得 n0=n2+1
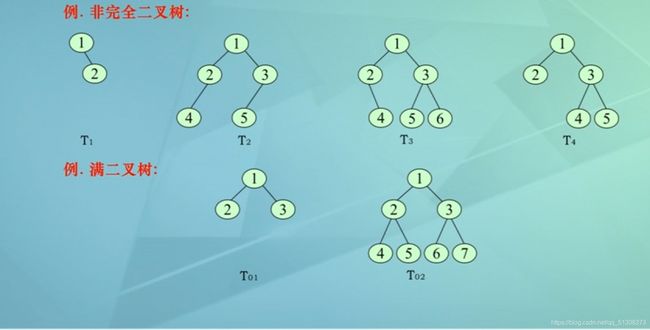
4.满二叉树
由性质2可知,深度为k的二叉树至多有2^k-1个结点。那么何时二叉树的结点可达最大值呢?
答:当每一层的结点数都达到最大,除最下层的叶子之外,其他每个结点都有2个孩子
故:满二叉树(full binary tree):深度为k且有2^k-1个结点的二叉树
(1)特点:
①每一层上结点数都达到最大,叶子结点都在第k层
②度为1的结点n1=0
③n个结点的满二叉树的深度=log2(n+1)(计算可得)
(2)顺序编号的满二叉树
从根结点起,从上到下逐层(层内从左到右)对二叉树的结点进行连续编号
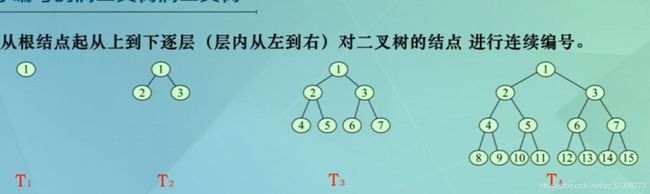
设满二叉树有n个结点,编号为1,2,…,n,则有如下特征
①左小孩为偶数,右小孩为奇数
②结点i的左小孩是2i,2i<=n
结点i的右小孩是2i+1,2i+1<=n
结点i的双亲是[i/2],意为取整,2<=i<=n
④结点i的层号=[log2 i]+1(向下取整) = [log2(i+1)](向上取整),1<=i<=n]
5.完全二叉树(顺序二叉树)
(1)定义:深度为k有n个结点的二叉树,当且仅当每一个结点都与同深度的满二叉树中的结点一一对应
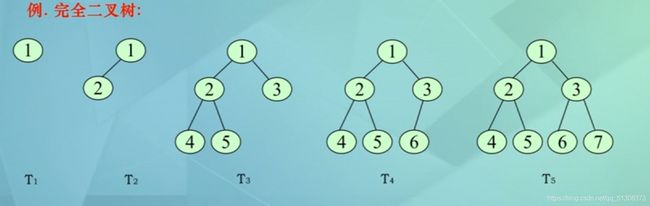
T4、T5是深度为3的完全二叉树
如:T1和T01结点并不一一对应,T1中结点2在T01中应为结点3
(2)性质
①任意结点i,其左右子树的深度分别表示为Lhi和Rhi,则Lhi-Rhi=0或1,即叶结点只可能出现在倒数两层上
②完全二叉树结点数n满足2^(k-1)-1 < n <= 2^k-1
③由②可得,结点数n的完全二叉树,其深度为[log2 n]+1 (向下取整)= [log2(n+1)] (向上取整)
设完全二叉树有n个结点,编号为1,2,…,n,则有如下特征:
①若i=1,则该结点为二叉树的根,无双亲,否则,编号为[i/2](向下取整)的结点为其双亲结点
如5的双亲是2
②若2i>n,则该结点无左孩子,否则,编号为2i的结点为其左孩子结点
若2i+1>n,则该结点无右孩子,否则,编号为2i+1的结点为其右孩子结点
如3没有右孩子结点
三、二叉树的存储结构
1.顺序结构
(1)使用一维数组存储完全二叉树
#define MAX_TREE_SIZE 100//二叉树的最大结点数
{
typedef TElemType SqBiTree[MAX_TREE_SIZE];//0号单元存储根结点
} SqBiTree bt;
顺序存储特点:用一组地址连续的存储单元,以层序顺序存放二叉树的数据元素,结点的相对位置蕴含着结点之间的关系

(2)使用一维数组存储一般二叉树
一般二叉树:按完全二叉树形式存储,没结点处用0表示,表示“虚结点”

深度为k的二叉树,需长度为 (2^k-1 )的一维数组。空间利用率为k/(2^k-1).
当k=10时,空间利用率只有0.0098,极低
缺点:①浪费空间
②插入、删除不便
小结:完全二叉树的顺序存储较为有效,但大多数一般二叉树则用链式存储比较高效
2.链式存储
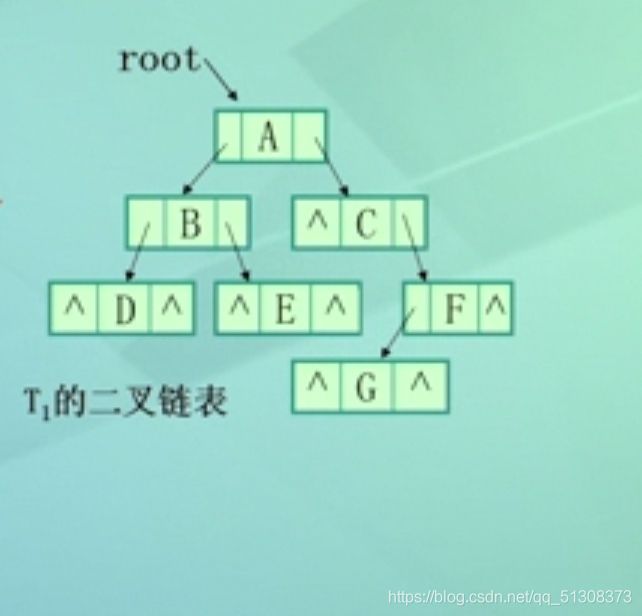
(1)二叉链表
①根结点指针必须保存
typedef struct BiTNode//结点结构
{
TElemType data;
struct BiTNode *lchild,*rchild;//左右孩子的指针
}BiTNode *BiTree;//指向该结点结构的指针类型
(2)三叉链表
在二叉链表这样的结构中,若要访问双亲,则只能一层层访问上去,要通过漫长的搜索,故此提出三叉链表,增加双亲指针
typedef struct TriTNode//结点结构
{
TElemType data;
struct TriTNode *lchild,*rchild;//左右孩子的指针
}TriTNode *TriTree;//指向该结点结构的指针类型
也可采用静态链表
//静态链表
struct SBiTNode
{
ELemType data;
int lchild,rchild;//表示左右孩子在数组中的单元号
}SBiTree[n+1];
四、二叉树的遍历
1.遍历二叉树
(1)遍历:按某种规则访问二叉树的每一个结点一次,且仅一次的过程
注:遍历是任何类型均有的操作,对线性结构而言,只有一条搜索路径(因为每个结点均只有一个后继)
(2)二叉树是非线性结构,每个结点可能有两个后继,则存在如何遍历,按什么样的搜索路径遍历的问题。
(3)一次遍历后,使树中结点的非线性排列,按访问的先后顺序变为某种线性排列
遍历是树结构插入、删除、修改、查找等运算的基础
(4)二叉树有多种不同的遍历规则,为直观的描述,引入几个符合:
①D——访问根结点,输出根结点
②L——递归遍历左二叉树
③R——递归遍历右二叉树
(5)遍历规则(方案)
①先左后右:
DLR——先序遍历(先根,preorder)
LDR——中序遍历(中根,inorder)
LRD——后序遍历(后根,postorder)
②先右后左:
DRL——逆先序遍历
RDL——逆中序遍历
RLD——逆后序遍历
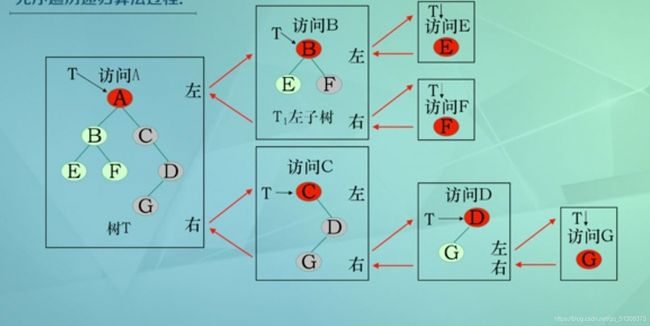
2.先序遍历
(1)先序遍历二叉树递归定义:
若二叉树为空,则遍历结束,否则,执行下列步骤:
①访问根结点
②先序遍历根的左子树
③先序遍历根的右子树
(2)先序遍历递归算法(基于二叉链表)
//先序遍历递归算法
typedef struct BiTNode *BiTree;//定义二叉结点指针类型
status reOrderTraverse(BiTree T,status(*visit)(TElemType &e))//第一个参数是二叉树的根结点指针,第二个为指向结点访问函数visit的函数指针
{
//先序遍历二叉树
if (T){
//判断当前二叉树是否为空
visit (T->data);//,调用visit函数访问当前根结点
PreOrderTraverse(T->lchild,visit);//遍历左子树
PreOrderTraverse(T->rchild,visit);//遍历右子树
}
}
3.中序遍历
(1)中序遍历二叉树递归定义:
若二叉树为空,则遍历结束,否则,执行下列步骤:
①中序遍历根的左子树
②访问根结点
③中序遍历根的右子树
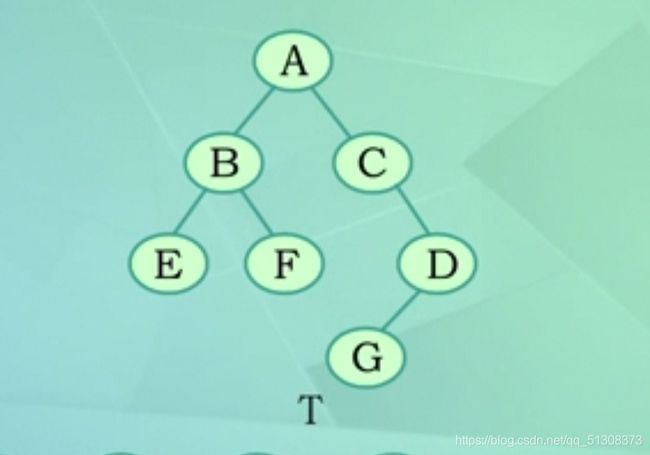
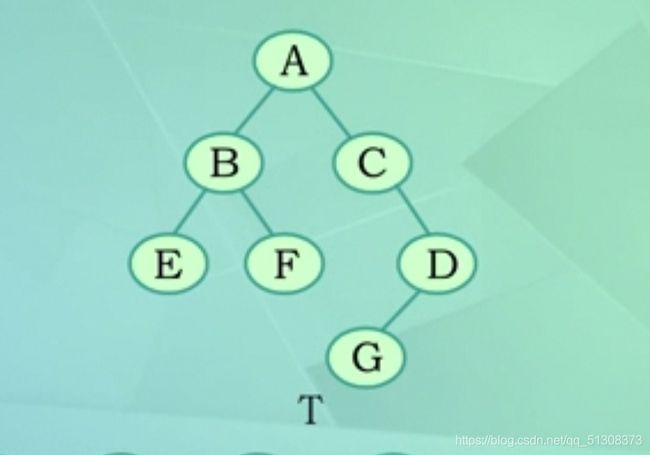
则顺序为:EBFACGD
(2)中序遍历递归算法
//中序遍历递归算法
typedef struct BiTNode *BiTree;//结点指针类型
void InOrderTraverse(BiTree T)//T是指向二叉链表根结点的指针
{
if(T)
{
InOrderTraverse(T->lchild);//递归访问左子树
printf("%c",T->data);//访问结点
InOrderTraverse(T->rchild);//递归访问右子树
}
return ;
}
4.后序遍历
(1)后序遍历二叉树递归定义:
若二叉树为空,则遍历结束,否则,执行下列步骤:
①后序遍历根的左子树
②后序遍历根的右子树
③访问根结点

则顺序为:EFBGDCA
(2)后序遍历递归算法
//后序遍历递归算法
typedef struct BiTNode *BiTree;//结点指针类型
void PostOrderTraverse(BiTree T)//T是指向二叉链表根结点的指针
{
if(T)
{
PostOrderTraverse(T->lchild);//递归访问左子树
PostOrderTraverse(T->rchild);//递归访问右子树
printf("%c",T->data);//访问结点,visit(T->data)
}
return ;
}
5.非递归算法(中序遍历)
(1)递归算法缺点:简明精炼,但效率极低;某些高级语言不支持递归。
故此处给出非递归算法的中序遍历,其余两种遍历可参照。
(2)非递归算法思想:运用栈
①设置栈s存放所经过的根结点指针信息;初始化s
②遇到根结点并不访问,而是入栈
③中序遍历它的左子树
④左子树遍历结束后,将根结点指针退栈,并访问根结点
⑤中序遍历它的右子树
⑥当需要退栈时,若栈为空则结束
//非递归中序遍历
Status InOrderTraverse (BiTree T,status(*visit)(TElemType &e))
{
InitStack(S);//s为存储二叉树结点的指针栈
push(S,T);//根指针进栈(空指针也进栈)
while (!StackEmpty(S))//栈非空,即遍历没结束
{
while (GetTop(S,p) && p)//只要栈顶为非空指针
{
push (S,p->lchild);//向左走到尽头
}
pop (S,p);//空指针退栈
if (!StackEmpty(S))//访问其结点及右子树
{
pop(S,p);
visit(p->data);//访问p结点
push(S,p->rchild);//p的右孩子压入栈中
}
}
return OK;
}
(3)该算法特点
①根先进栈,左孩子紧随其后进栈,右孩子在根出栈后入栈
②每个结点都进一次和出一次栈,且总访问栈顶元素,故时间复杂度为O(n)。最坏时,空间复杂度为O(n)
6.层序遍历算法
(1)算法思想:
①按从上往下逐层,同层从左至右的次序访问各结点
②访问根之后,通过根访问其左孩子,然后右孩子
问:左右孩子有时并不能紧随其后被马上访问,如何暂存没访问过的结点呢?
(2)使用队列进行循环处理
基本思路:
①若队列非空,队头结点出队,并访问该结点
②若该结点左右孩子非空,则依次进队
//层序遍历算法
void LayerOrder(BiTree T)//输入参数为根结点指针T
{
InitQueue(Q);//初始化队列
if(T)
{
EnQueue(Q,T);//T非空则入队
}
while (!QueueEmpty(Q))//队列非空
{
DeQueue(Q,&p);//队头结点出队(送入p)
visit(p);//出队后立刻访问该结点
//以下为孩子入队,当孩子为空时空指针不入队
if (p->lchild)
EnQueue(Q,p->lchild);//p的左孩子入队
if (p->rchild)
EnQueue(Q,p->rchild);//p的右孩子入队
}
}
五、二叉树的遍历的应用
1.建立二叉树的存储结构
(1)同一先序序列,对应的树不唯一
如:ADEFGBC,可产生树T1、T2,但加入“空”后,则可唯一确定

(2)算法:创建二叉树
输入:带空节点的二叉树的先序序列
输出:二叉树的根指针
#define leng sizeof(BiTnode)//结点所占空间大小
(3)递归实现:类似于先序遍历,修改一下生成二叉链表即可
//创建二叉树(递归)
Status CreateBiTree (BiTree &T)//按先序次序输入二叉树结点的值(空格符表示空树),构造二叉链表
{
scanf (&ch);//输入第一个字符
if (ch==' ')
T = NULL;//置根结点为空
else{
if (!(T = (BiTNode*)malloc(sizeof(BiTNode))))//建立二叉链表根结点
exit(OVERFLOW);//空间不足则失败
T->data = ch;//生成根结点
CreateBiTree(T->lchild);//构造左子树
CreateBiTree(T->rchild);//构造右子树
}
return OK;//c语言程序不支持引用参数,如何将T返回给主调函数 。需引入指针
}
2.基于遍历序列构造二叉树
(1)举例:已知二叉树的中序序列和后序序列分别是BDCEAFHG和DECBHGFA,生成这棵二叉树
分析:
①由后序遍历特征,根结点必在后序序列尾部(A)
②由中序遍历特征,根结点必在其中间,而且其左部必全部是左子树的子孙(BDCE),其右部必全部是右子树的子孙(FHG)
③继而,根据后序中的DECB子树可确定B为A的左孩子,根据HCF子串可确定F为A的右孩子;依次类推,便可确定序列中每个符合对应结点的位置
3.求二叉树的深度(后序遍历)
(1)算法基本思想:基于后序遍历,需分别求得左右子树的深度,再加1
d=max(dl,dr)+1
(2)算法实现
//求二叉树的深度
int Depth(BiTree T)
{
if (!T)//判空
depthval = 0;
else{
//仿造后序遍历
//递归调用
depthLeft = Depth(T->lchild);//输入左子树的根指针,求深度
depthRight = Depth(T->rchild);//输入右子树的根指针,求深度
depthval = 1 + (depthLeft > depthRight ? depthLeft : depthRight);//判断表达式,取左右深度中最大深度
}
return depthval;//输出深度
}
总结
ps:(再一点废话)(虽然咕咕了半个月,但是这一篇巨巨粗长!!!)
因为树不再是单纯的线性结构,自本篇开始,会有大量插图,便于大家理解。另外,代码会做一定精简,重在解释概念。树这部分有好多拓展的东西(包括算法和思想等等),这一篇只涉及基本的树,在下一篇中会讲到哈夫曼树及线索二叉树。
ps:代码非原创。
如有错误,欢迎指正。