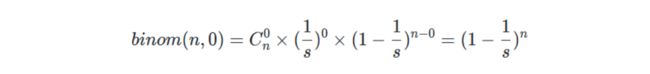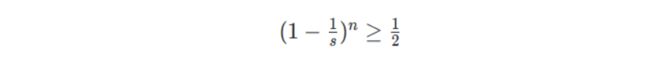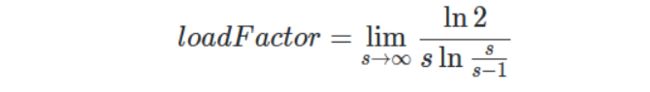手写实现HashMap——源码梳理
Java手写实现HashMap——替换红黑树
由于我之前封装实现过一棵红黑树
RBTree,在此次实现HashMap中,我将会将我实现的红黑树整合到HashMap中。算是自己的一个小小的尝试吧。
哈希
哈希,又叫hash, 指的是把一个任意长度的输入转为一个固定长度的输出。这是一种压缩映射,由于是将一个任意长度的输入转为一个固定长度的输出,所以,输入域大于输出域,那么就可能出现两个不同的输入会出现相同的输出。这就叫做哈希冲突。
hash冲突:
可以简单的理解为,将10个及以上的苹果放进9个格子中,如果要将这些苹果全部放进到这9个格子中,那么在至少有一个格子中存在两个或者以上的苹果。
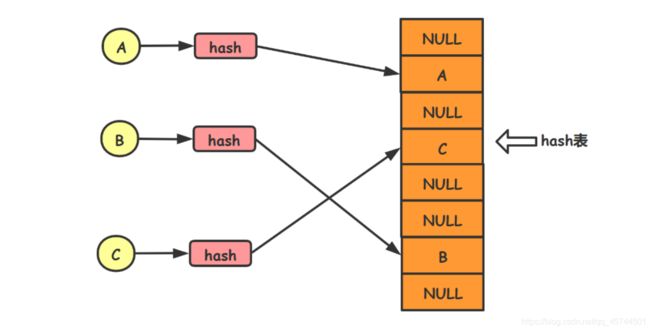
哈希表(散列表)
他是一种根据关键码值而直接访问的数据结构,他对目标对象的关键码值进行哈希散列操作后会得到一个哈希值,而这个值对应的就是该目标对象在该散列表中的下标索引,如此,便可以根据得到的下标索引直接访问或者存储目标对象。
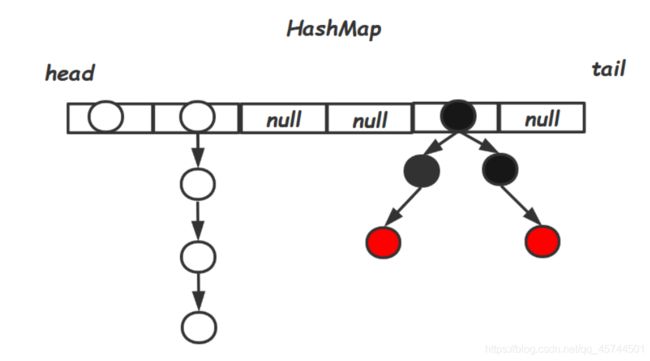
HashMap的数据结构
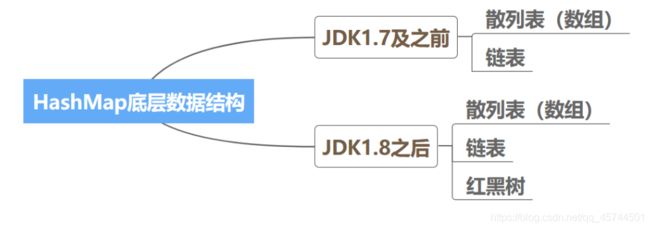
在Java中,JDK1.7之前的数据结构相对比较简单,就是两个比较基础的数据结构:散列表(数组)和链表 。而在JDK1.8之后,对其的数据结构进行了一次比较大的更改,变为了:散列表(数组) 、 链表和 红黑树。
散列表
/**
* 用于存储数据的散列表 ,但是不会被序列化
*/
private transient Node<Key, Value>[] table;
Node 节点
/**
* 用于存储数据的最基本的节点对象,作为后续的 TreeNode 的 superClass
*
* @param 键
* @param 值
*/
static class Node<Key extends Comparable<Key>, Value> {
final int hash;
final Key key;
Value value;
Node<Key, Value> next;
Node<Key, Value> prev;
}
红黑树的树节点TreeNode
protected class TreeNode extends MyHashMap.Node {
Key key;
Value value;
TreeNode left;
TreeNode right;
TreeNode parent;
int amount;
boolean color;
}
这样设计的目的是为了在向 HashMap中添加或者删除元素的时候,如果出现了哈希冲突或者需要对存储的结构进行调节(比如扩容)的时候,我们可以比较方便的进行类型转换,特别是在进行红黑树需要调节为链表的时候,后面我们可以很清晰的看到,在红黑树的内部实际上是还维护着一个链表的,这样以至于在转链表的时候更加方便。
HashMap的常量值
以下是在实现 HashMap中需要的一些常量值,在注释中给出了常量的含义,具体的使用和作用在后续的核心方法实现中会体现。
/***************常量*****************/
private static final long serialVersionUID = 362498820763181265L;
/**
* 默认的构造初始大小为 1 << 4 = 16 实际是hashMap中散列表的初始大小
*/
private static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
/**
* 默认的负载因子 为 0.75 当构造函数中没有指定该项参数的时候的默认值
* 源码文档的解释为,在负载因子为0.75的情况下,产生hash冲突的概率是最小的
*/
private static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* 树化阈值,当散列表中的一个槽位slot对应的链表的长度达到 8 之后,就会执行树化操作
*/
private static final int TREEIFY_THRESHOLD = 8;
/**
* 红黑树转链表的阈值,当散列表中的槽位对应的节点数目为6,且当前的数据结构为红黑树,则会发生树-->链表的操作
*/
private static final int UNTREEIFY_THRESHOLD = 6;
/**
* 该属性值和{@see TREEIFY_THRESHOLD} 一起决定是否需要将节点进行树化操作
* 当前散列表中的节点总数一定要达到 64 ,才被允许进行树化操作,否则即使
* TREEIFY_THRESHOLD的值 > 8 ,仍然不能进行树化操作
*/
private static final int MIN_TREEIFY_CAPACITY = 64;
static final int MAXIMUM_CAPACITY = 1 << 30;
HashMap 的初始化
我们在使用一个 HashMap的时候,我们一般会先创建一个该类的实例。
Map<Key,Value> map = new HashMap<>();
现在我们就来剖析具体的流程以及代码实现。
构造函数
在官方的 HashMap的实现中,采用的是如下的几个构造函数:
/**
* 给定参数的构造方法,给定初始化大小以及负载因子
*
* @param initialCapacity 初始化大小(后面会被处理成2的次方数)
* @param loadFactor 负载因子
*/
public MyHashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0) {
initialCapacity = DEFAULT_INITIAL_CAPACITY;
} else if (initialCapacity > MAXIMUM_CAPACITY) {
initialCapacity = MAXIMUM_CAPACITY;
}
this.threshold = tableSizeFor(initialCapacity);
if (loadFactor < 0 || Float.isNaN(loadFactor)) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
} else {
this.loadFactor = loadFactor;
}
}
public MyHashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public MyHashMap() {
this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR);
}
可以清晰地看到,提供了3个构造函数,用户在创建Map实例的时候,可以显式地指定初始化的容量大小(散列表的长度),以及负载因子。
细细看一下,我们可以发现,最核心的构造函数为:
public MyHashMap(int initialCapacity, float loadFactor)
看到代码实现,发现其实他并没有做什么事情,只是对一些属性值进行了初始化而已,并没有实际申请存储数据的散列表(table)。后面我们在实现put方法的时候,我们可以清晰地看到,他其实是在第一次往 HashMap中添加元素的时候,根据在此方法中确定的初始化容量大小来创建散列表的实例的,可见,他实际一种 懒加载机制。
我们看到,在对 initialCapacity的判断处理时,首先是对其数据的合法性进行了判断,如果 < 0 则赋值为默认初始化大小,如果比默认的最大容量值大,则赋值为最大默认容量。然后调用了 tableSizeFor(int cap);方法:
tableSizeFor
这个方法实际是对输入的值进行规范化处理,将其处理为一个超过给定值的最小2的次幂的整数。
这个算法设计得十分巧妙,充分利用了位运算,学到了,学到了。
/**
* 返回一个 >= cap的最小的 2 的次方数
*
* @param cap 给定的容量大小
* @return >= cap的最小的 2 的次方数
*/
private static int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 16;
n |= n >>> 8;
n |= n >>> 4;
n |= n >>> 2;
n |= n >>> 1;
return (n < 0) ?
1 :
(n >= MAXIMUM_CAPACITY) ?
MAXIMUM_CAPACITY : n + 1;
}
在这里,先留个问题:
为何要将散列表的长度设置为2的次幂数?
小结
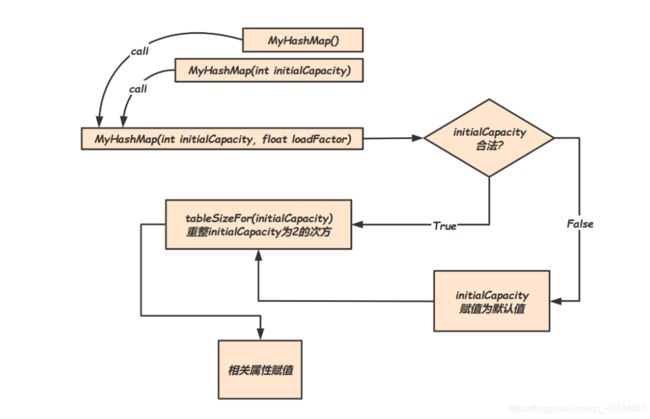
这里我们就可以对 HashMap的初始化操作有一个比较细致的认识,我们可以通过下面这个图来描绘这个过程:
HashMap 的hash值扰动
之前我们提过,在进行哈希的时候,会出现哈希冲突的情况,在这种情况下,我们就需要处理这种冲突,在 HashMap中,我们采用的是链表和红黑树来解决这个冲突,但是在处理这种冲突时,会带来两个问题:
- 散列表的空间没有得到有效的利用
- 需要开辟新的存储结构,在创建结构时,需要一定空间和时间
这两个问题都是我们应该尽量避免的。
于是就有了下面这个扰动函数,把hashCode变得更加的散列,使得key产生哈希冲突的概率降低,进而提高该map的空间利用率和效率。
/**
* rehash:将 key 的哈希值的低 16 位和高 16 位异或得到新的 hash 值
* 用于减少哈希冲突,使得key的哈希值的高16位的信息也被利用
* 尽量地使得 hash 值更加散列
*
* @param key 键
* @return 新的 hash
*/
protected static int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
HashMap的寻址算法
根据已经进行散列加强后的hash值得到在对应在 HashMap中的散列表的索引位置下标:
/**
* @param hash 传入的 hash 值
* @return 该 hash 值对应于散列表中的索引位置
*/
final int getIndex(int hash) {
return (table.length - 1) & hash;
}
这一步的算法设计从代码角度来看,就是一个简单的按位 &运算。实则十分巧妙呢!
我们在对原本对象的
hashCode进行了散列加强后,得到的是一个整型数据,要将其映射到一个长度有限的散列表中,我们可以采用将hash值%散列表的长度length得到的值作为其在散列表中的位置。但是巧妙的点在于:
当
length为2的次方数的时候,hash % length == hash & (length - 1)。采用后者的计算方式,效率明显高于前者,因为取模运算最后在底层硬件的运算时,会转为加法来计算,我们知道,在底层硬件的门电路实现加法器时需要多个门电路,对于取模,需要比较多的时钟周期才能得到结果;如果采用后者的话,理论上只需要一个与门,和一个减法器就可以完成运算并得到结果,执行效率更高。这在一方面解释了为何
HashMap中散列表的长度需要设计为2的次方数。
HashMap的扩容机制
扩容模式
达到扩容条件的时候,将散列表的长度扩大一倍。然后将现有元素迁移到合适的位置,即可。
这个机制也决定了散列表的长度要设置为2的次方数。
扩容阈值
在JDK中的 HashMap的扩容阈值由负载因子 loadFactor与散列表的长度 length的乘积决定。举个例子:
当散列表的长度为16,负载因子为0.75,那么当map中的元素超过了16*0.75=12就会触发扩容机制。
负载因子
在官方的注释的解释中:提到默认的 loadFactor=0.75f是一个折中的选择,在保证有较高的空间利用率的前提下,还能够保证比较高的查询效率。
关于负载因子为何默认值为0.75:
JDK1.7源码上的注释
一般而言,默认负载因子为0.75的时候在时间和空间成本上提供了很好的折中。太高了可以减少空间开销,但是会增加查找复杂度。我们设置负载因子尽量减少rehash的操作,但是查找元素的也要有性能保证。
JDK1.8的解释:
Because TreeNodes are about twice the size of regular nodes, we
use them only when bins contain enough nodes to warrant use
(see TREEIFY_THRESHOLD). And when they become too small (due to
removal or resizing) they are converted back to plain bins. In
usages with well-distributed user hashCodes, tree bins are
rarely used. Ideally, under random hashCodes, the frequency of
nodes in bins follows a Poisson distribution
(http://en.wikipedia.org/wiki/Poisson_distribution) with a
parameter of about 0.5 on average for the default resizing
threshold of 0.75, although with a large variance because of
resizing granularity. Ignoring variance, the expected
occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
factorial(k)). The first values are:
0: 0.60653066
1: 0.30326533
2: 0.07581633
3: 0.01263606
4: 0.00157952
5: 0.00015795
6: 0.00001316
7: 0.00000094
8: 0.00000006
more: less than 1 in ten million
因为TreeNode的大小约为链表节点的两倍,所以我们只有在一个链表已经有了足够节点的时候才会转为tree(参考TREEIFY_THRESHOLD)。并且,当这个hash桶的节点因为移除或者扩容后resize数量变小的时候,我们会将树再转为链表。如果一个用户的数据他的hashcode值分布十分好的情况下,就会很少使用到tree结构。在理想情况下,我们使用随机的hashcode值,loadfactor为0.75情况,尽管由于粒度调整会产生较大的方差,桶中的Node的分布频率服从参数为0.5的泊松分布。下面就是计算的结果:桶里出现1个的概率到为8的概率。桶里面大于8的概率已经小于一千万分之一了。
这个东西因为来自jdk1.8,而且提到了0.75,没有好好理解这段话的意思的话,很容易就认为这是在阐释0.75是怎么来的,然后就简单的把泊松分布给强关联到了0.75上去。然而,**这段话的本意其实更多的是表示jdk1.8中为什么拉链长度超过8的时候进行红黑树转换。**这个泊松分布的模型其实是基于已经默认因子就是0.75的模型去模拟演算的。
虽然不懂,但是以后有人问直接甩他一个泊松分布就行了,直到–我忘了泊松分布的知识点了。其实也好理解,红黑树是1.8之后加进来的,所以jdk源码者并没有特地为我们解释下为啥当时设计了0.75,而是更多是想解释一些关于加入红黑树之后一些设计的原因。
HashMap的二项分布
那么,这个和我们的这个负载因子有什么关系呢?我们先针对一下特性,来做一下思路的转换类比:
- 实验只有2种结果
- 我们往hash表put数据可以转换为key是否会碰撞?碰撞就失败,不碰撞就成功。
- 实验相互独立
- 我们可以设想,实验的hash值是随机的,并且他们经过hash运算都会映射到hash表的长度的地址空间上,那么这个结果也是随机的。所以,每次put的时候就相当于我们在扔一个16面(我们先假设默认长度为16)的骰子,扔骰子实验那肯定是相互独立的。碰撞发生即扔了n次有出现重复数字。
- 成功的概率都是一样的
- 这就是我难以理解的地方,这个地方可以说的过去,也可以说不过去。
- 说的过去
- 每次一put的前面的位置我们不知道会在哪!可能前面一直都在一个位置上,那么我们理论上的概率一直都是 1 16 \frac{1}{16} 161。我们可以姑且抽象的认为概率p为 1 s \frac{1}{s} s1(设长度为s)。
- 需要说明的是:这里我并不确定是否合理,这也是过程中我认为不太严谨的地方。
- 说不过去
- 但是每次扔的大可能不会在同一个位置上,所以概率每次都会不一样,但是这个不一样又是我们无法估量和猜测的。
然后,我们的目的是啥呢?
就是掷了k次骰子,没有一次是相同的概率,需要尽可能的大些,一般意义上我们肯定要大于0.5(这个数是个理想数,但是我是能接受的)。
于是,n次事件里面,碰撞为0的概率,由上面公式得:
这个概率值需要大于0.5,我们认为这样的hashmap可以提供很低的碰撞率。所以:
这时候,我们对于该公式其实最想求的时候长度s的时候,n为多少次就应该进行扩容了?而负载因子则是 n / s n/s n/s的值。所以推导如下:
这也就是为什么stackoverflow上说接近于ln2的原因了。然后再去考虑hashmap一些内置的要求:
- 乘16可以最好一个整数。
那么在0.5~1之间找一个小数,满足这要求的只有0.625(5/8),0.75(3/4),0.875(7/8)。0.75是最为折中的一个选择。
HashMap扩容的元素迁移
当在往散列表中添加元素的时候,当元素的数量达到了扩容阈值,那么就会进行扩容,扩容中涉及到的一个问题就是如何将已经在map中存放着的现有数据进行合理而高效地迁移。
现在我们来分析这个问题:
什么情况下才需要进行元素的迁移?很简单,就是当散列表的一个桶位中存放着多个元素,即是已经链化或者树化。其他的操作不用进行操作,放在扩容的散列表的相同索引下的桶位中就可以了。
高位链和低位链
在讨论什么是高位链和低位链之前,我们先回顾一下寻址算法:
index = hash & (table.length - 1), 为了更好地理解,我这里举个具体的例子:
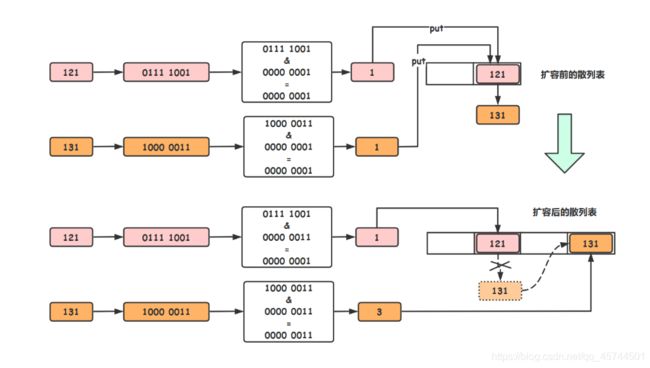
假设现在的散列表的长度为2,现在有两个元素的hash值分别为121和131(实际hash数字很大,这里为了简单,设置的数仅供演示).
从上图中可以比较清楚看到,在扩容之前,121和131同占用着散列表的1号位置桶位,形成了链表。扩容后,131被迁移到了新散列表的3号桶位,新的散列表中没有链化,访问效率和数组一致。
但是,是怎样确定是131迁移而不是121迁移呢?
这就引出了高位链和低位链的概念:其在代码中体现为:
以上述情况为例子:
121对应的8位二进制码为0111 1001,131对应的8为二进制码为1000 0011,在没有扩容之前,他们低1位是一致的均为1,因此在和 table.length - 1 = 2 - 1 = 1 = 0000 0001 按位 &之后得到的值是一致的,产生hash冲突,为解决冲突,使用链表的结构来存储数据。扩容之后,table.length - 1 = 4 - 1 = 3 = 0000 0011 ,此次我们发现121和131的低2位是不一样的,121为0,131为1,于是我们将高位为1的节点称为高位节点,由高位节点构成的链表称为高位链,反之称为低位链。
迁移
在确定好高位链和低位链后,就可以进行数据的迁移了。在扩容后的散列表中,低位链迁移到和之前一样索引的桶位,而高位链迁移到 oldIndex + oldTable.length位置的桶位去。
如果在进行数据迁移的时候,桶位中的数据结构已经是红黑树结构了,那怎样确定高位链和低位链呢????
红黑树的节点 TreeNode他是Node的子类,在进行添加红黑树节点和删除红黑树节点的时候,其实内部是还维护着一个链表的,这样的话,就比较方便的进行高低位链表的拆分,拆分完成后,移动新的桶位去,最后还得检查元素的数量,看其是否达到了树化或者链化的条件,最后进行一次结构重整后,整个扩容就结束了。
HashMap添加元素
我封装的 HashMap中提供了一下几个API方法调用:
/**
*
* @param key 需要判断的 key
* @return true if in the map,otherwise false
*/
public boolean containsKey(Object key) {
return getNode(key) != null;
}
/**
* This is the default put method ,when the key you put in
* has already in the map ,then the program will replace the old
* value with the new value you put in.
*/
public Value put(Key key, Value value) {
return put(key, value, true);
}
/**
* This put method allow you to choose the operation when there
* occurs the hash conflict(the key has already in the map) with param
* flag : true --> replace the old value with new value
* : false--> refuse to add this item into the map
* and throws the Exception
*/
public Value put(Key key, Value value, boolean flag) {
return putValue(key, value, flag);
}
实际的实现是在 putValue()方法中:
/**
* This method can make the key and the value you put in the
* function to a node , and the put in the data structure of the
* map ,and if the process is successfully executed ,then return
* the value.
* Attention : if the key you put has already in the map ,then you
* can choose to add it or not with the param flag
* (true to add and false to refuse)
*
* @param key 待插入到 HashMap 的元素的 key
* @param value 待插入到 HashMap 的元素的 value
* @param flag 遇到已经存在的 key , true add or refused to add
* @return the value that you put in the map.
*/
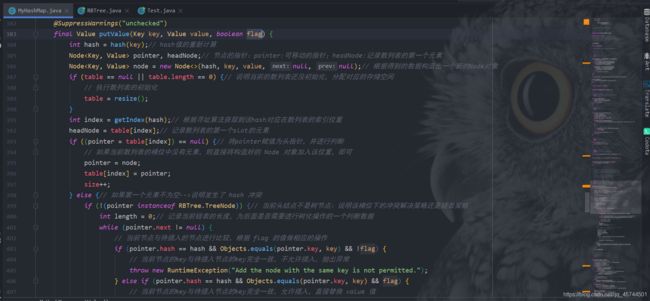
@SuppressWarnings("unchecked")
final Value putValue(Key key, Value value, boolean flag) {
int hash = hash(key);// hash值的重新计算
Node<Key, Value> pointer, headNode;// 节点的指针:pointer:可移动的指针;headNode:记录散列表的第一个元素
Node<Key, Value> node = new Node<>(hash, key, value, null, null);// 根据得到的数据构造出一个新的Node对象
if (table == null || table.length == 0) {
// 说明当前的散列表还没初始化,分配对应的存储空间
// 执行散列表的初始化
table = resize();
}
int index = getIndex(hash);// 根据寻址算法获取到该hash对应在散列表的索引位置
headNode = table[index];// 记录散列表的第一个slot的元素
if ((pointer = table[index]) == null) {
// 将pointer赋值为头指针,并进行判断
// 如果当前散列表的桶位中没有元素,则直接将构造好的 Node 对象加入该位置,即可
pointer = node;
table[index] = pointer;
size++;
} else {
// 如果第一个元素不为空-->说明发生了 hash 冲突
if (!(pointer instanceof RBTree.TreeNode)) {
// 当前头结点不是树节点:说明该桶位下的冲突解决策略还是链表策略
int length = 0;// 记录当前链表的长度,为后面是否需要进行树化操作的一个判断数据
while (pointer.next != null) {
// 当前节点与待插入的节点进行比较,根据 flag 的值做相应的操作
if (pointer.hash == hash && Objects.equals(pointer.key, key) && !flag) {
// 当前节点的key与待插入节点的key完全一致,不允许插入,抛出异常
throw new RuntimeException("Add the node with the same key is not permitted.");
} else if (pointer.hash == hash && Objects.equals(pointer.key, key) && flag) {
// 当前节点的key与待插入节点的key完全一致,允许插入,直接替换 value 值
pointer.value = value;
return pointer.value;
}
length++;// 链表长度 + 1
pointer = pointer.next;// pointer 指针后移一位
}
// 当 while loop 结束后,当前pointer为链表的尾节点,且在之前的节点中没有与 key 一致的情况
// 没有出现 hash 冲突,直接在链表的尾部插入当前构造的新节点,即可
pointer.next = node;
node.prev = pointer;
pointer = pointer.next;
length++;// 添加成功:链表长度 + 1
size++;
if (size > MIN_TREEIFY_CAPACITY && length > TREEIFY_THRESHOLD) {
// 当前 Map中的键值对儿的数量达到了树化阈值,
// 且链表的长度达到了树化阈值,以头结点进行树化操作
table[index] = treeify(headNode);
}
} else {
// 当前已经为红黑树的存储数据结构,直接调用红黑树的插入方法插入即可
pointer = Tree.put((RBTree<Key, Value>.TreeNode) headNode, key, value, flag);
size++;
}
}
return pointer.value;
}
在这里我将我自己之前封装的红黑树融入了到了这个方法中,并且为了适应hashMap的结构,也对红黑树的结构进行了微调,最终还是比较顺利地将红黑树添加进去了。
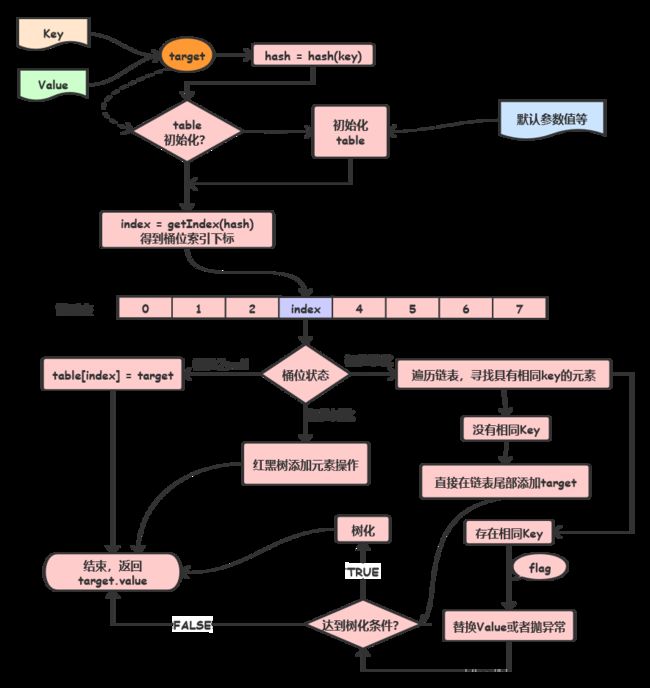
代码的实现比较抽象,这里我再补上一张图吧,简单梳理一下添加元素的过程吧。