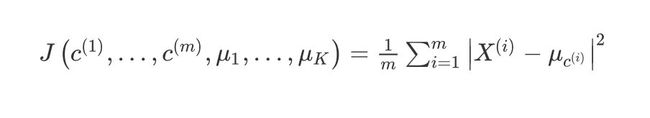吴恩达机器学习-8-聚类知识

公众号：尤而小屋
作者：Peter
编辑：Peter

吴恩达机器学习-8-聚类

本周的主要知识点是无监督学习中的两个重点：聚类和降维。本文中首先介绍的是聚类中的K均值算法，包含：

• 算法思想
• 图解K-Means
• sklearn实现
• Python实现

无监督学习unsupervised learning

无监督学习简介

聚类和降维是无监督学习方法，在无监督学习中数据是没有标签的。

比如下面的数据中，横纵轴都是$x$，没有标签（输出$y$）。在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，快速这个数据的中找到其内在数据结构。

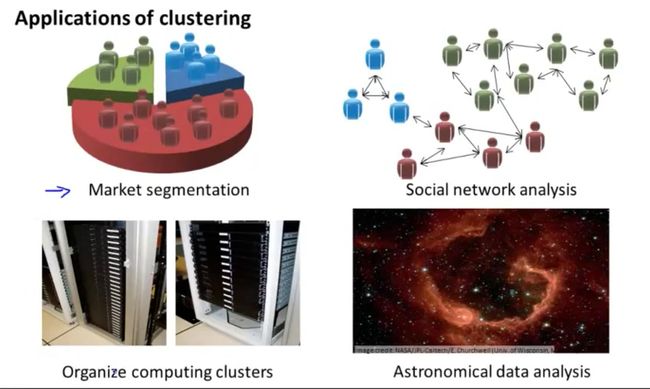
无监督学习应用

• 市场分割
• 社交网络分析
• 组织计算机集群
• 了解星系的形成

聚类

聚类clustering

聚类试图将数据集中的样本划分成若干个通常是不相交的子集，称之为“簇cluster”。聚类可以作为一个单独过程，用于寻找数据内部的分布结构，也能够作为其他学习任务的前驱过程。聚类算法涉及到的两个问题：性能度量和距离计算

性能度量

聚类性能度量也称之为“有效性指标”。希望“物以类聚”。聚类的结果是“簇内相似度高”和“簇间相似度低”。

常用的外部指标是：

1. Jaccard 系数
2. FM 系数
3. Rand 系数

上述3个系数的值都在[0,1]之间，越小越好

常用的内部指标是：

1. DB指数
2. Dunn指数

DBI的值越小越好，Dunn的值越大越好。

距离计算

$x_i,x_j$的$L_p$的距离定义为：

$$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}}$$

规定：$p\ge 1$，常用的距离计算公式有

• 当$p=2$时，即为欧式距离，比较常用，即：

$$L_2(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2{)}^{\frac{1}{2}}$$

• 当$p=1$时，即曼哈顿距离，即：

$$L_1(x_i,x_j)=\sum _{l=1}^n(|x_i^{(l)}-x_j^{(l)}|)$$

• 当$p$趋于无穷，为切比雪夫距离，它是各个坐标距离的最大值：

$$L_{\infty }(x_i,x_j)=\underset{l}{\max }|x_i^{(l)}-x_j^{(l)}|$$

余弦相似度

余弦相似度的公式为：

$$\cos (\theta )=\frac{x^{T}y}{|x|\cdot |y|}=\frac{{\sum }_{i=1}^n{x}_i{y}_i}{\sqrt{{\sum }_{i=1}^n{x}_i^2}\sqrt{{\sum }_{i=1}^n{y}_i^2}}$$

Pearson皮尔逊相关系数

皮尔逊相关系数的公式如下：

$${\rho }_{XY}=\frac{\mathrm{cov}(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E\left[\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)\right]}{{\sigma }_X{\sigma }_Y}=\frac{{\sum }_{i=1}^n\left(x-{\mu }_X\right)\left(y-{\mu }_Y\right)}{\sqrt{{\sum }_{i=1}^n{\left(x-{\mu }_X\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y-{\mu }_Y\right)}^2}}$$

K-均值算法

算法思想

K-均值，也叫做k-means算法，最常见的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。 假设将数据分成n个组，方法为：

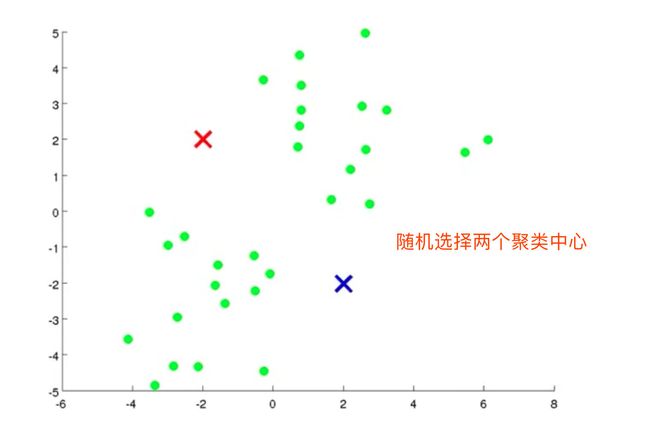
• 随机选择K个点，称之为“聚类中心”
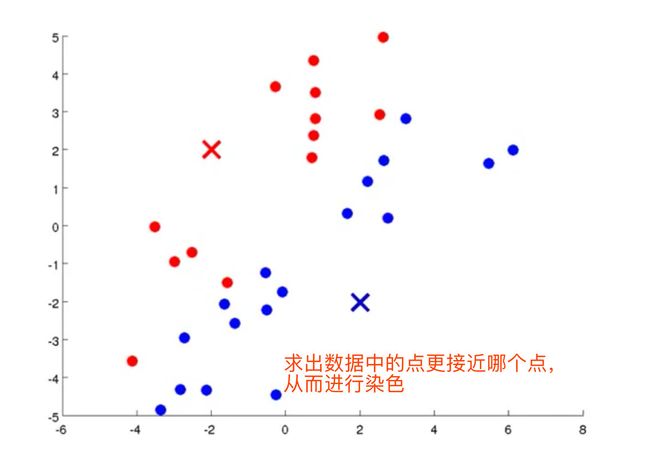
• 对于数据集中的每个数据，按照距离K个中心点的距离，将其和距离最近的中心点关联起来，与同个中心点关联的所有点聚成一类。
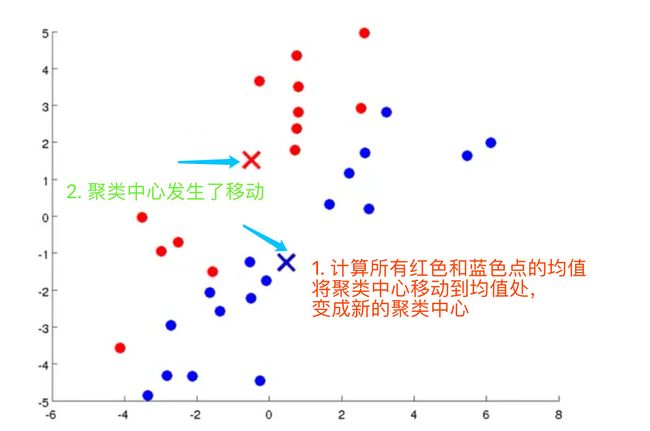
• 计算上面步骤中形成的类的平均值，将该组所关联的中心点移动到平均值的位置
• 重复上面两个步骤，直到中心点不再变化。

图解K-means

1. 给定需要划分的数据，随机确定两个聚类中心点
2. 计算其他数据和这两个中心点的距离，划入距离小的类中，假设两个类是$C_1,C_2$
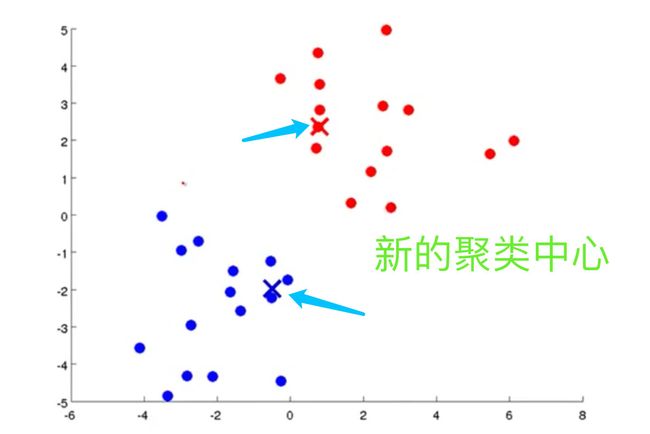
3. 确定上述步骤中两个类是$C_1,C_2$的均值，这个均值就是新的聚类中心
4. 重复：计算数据和这两个中心点的距离，划入距离小的类中，形成新的类；再确定新的聚类中心
5. 直至中心点不再变化，结束

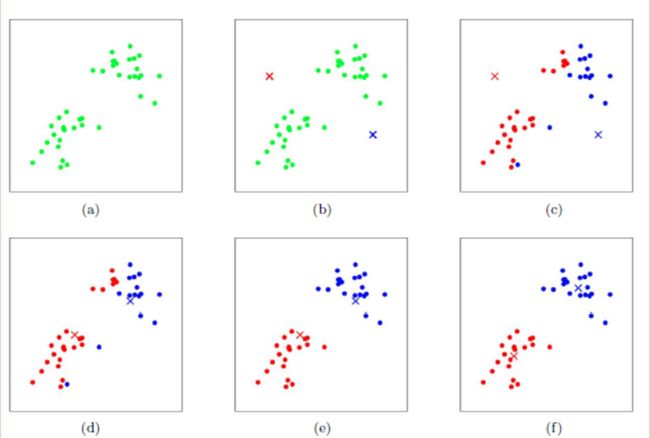
全过程

K-means算法过程

吴恩达视频的中的伪代码为

repeat {
     
  for i= to m
  #  计算每个样例属于的类
  c(i) := index (from 1 to K)  of cluster centroid closest to x(i)

 for k = 1 to K
  # 聚类中心的移动，重新计算该类的质心
 u(k) := average (mean) of points assigned to cluster K
}

西瓜书中的伪代码

优化目标Optimization Objective

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（畸变函数Distortion function） ：

$$J\left(c^{(1)},\dots ,c^{(m)},{\mu }_1,\dots ,{\mu }_K\right)=\frac{1}{m}\sum _{i=1}^m{\left|X^{(i)}-{\mu }_{c^{(i)}}\right|}^2$$

其中$u_{c^{(i)}}$代表的是$x^{(i)}$最近的聚类中心点。

优化目标就是找出使得代价函数最小的$c^{(1)},c^{(2)},\dots ,c^{(m)}$和${\mu }_1,{\mu }_2,\dots ,{\mu }_k$，即：

随机初始化

在运行K-均值算法的之前，首先要随机初始化所有的聚类中心点：

• 选择$K<m$，即聚类中心的个数小于训练样本的实例数量
• 随机训练$K$个训练实例，然后令K个聚类中心分别和这K个训练实例相等

关于K-means的局部最小值问题：

Scikit learn 实现K-means

make_blobs数据集

make_blobs聚类数据生成器make_blobs方法常被用来生成聚类算法的测试数据。它会根据用户指定的特征数量、中心点数量、范围等来生成几类数据。

主要参数

sklearn.datasets.make_blobs(n_samples=100, n_features=2,centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]

• n_samples是待生成的样本的总数
• n_features是每个样本的特征数
• centers表示类别数
• cluster_std表示每个类别的方差

import numpy as np
import matplotlib.pyplot as plt
# 导入 KMeans 模块和数据集
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 定义画布
plt.figure(figsize=(12,12))

# 定义样本量和随机种子
n_samples = 1500
random_state = 170

# X是测试数据集，y是目标分类标签0，1，2
X, y = make_blobs(n_samples=n_samples, random_state=random_state)

X
array([[-5.19811282e+00,  6.41869316e-01],
       [-5.75229538e+00,  4.18627111e-01],
       [-1.08448984e+01, -7.55352273e+00],
       ...,
       [ 1.36105255e+00, -9.07491863e-01],
       [-3.54141108e-01,  7.12241630e-01],
       [ 1.88577252e+00,  1.41185693e-03]])

y
array([1, 1, 0, ..., 2, 2, 2])

# 预测值的簇类
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
y_pred
array([0, 0, 1, ..., 0, 0, 0], dtype=int32)

X[:,0]  # 所有行的第1列数据
array([ -5.19811282,  -5.75229538, -10.84489837, ...,   1.36105255,
        -0.35414111,   1.88577252])

# 子图1的绘制
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("incorrrect Number of Blods")

transformation = [[0.60834549, -0.63667341],[-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
# 子图2的绘制
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")

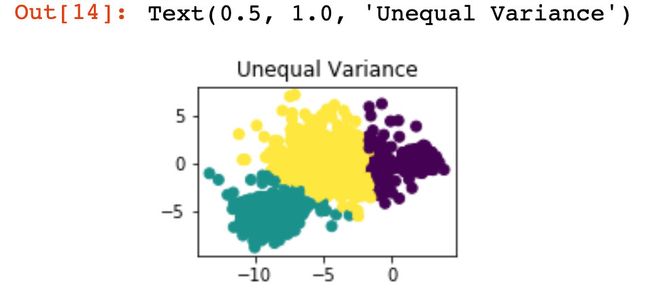
X_varied, y_varied = make_blobs(n_samples=n_samples,
                               cluster_std=[1.0,2.5,0.5],random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")

X_filtered = np.vstack((X[y == 0][:500],
                      X[y == 1][:100],
                      X[y == 2][:10]))
y_pred = KMeans(n_clusters=3,random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)
plt.scatter(X_filtered[:, 0],
           X_filtered[:, 1],
           c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show()

python实现K-means算法

这是在网上找到的一个基于Python找到的`K-means实验算法，学习使用