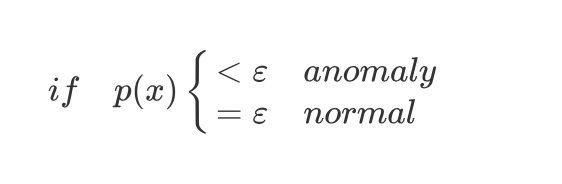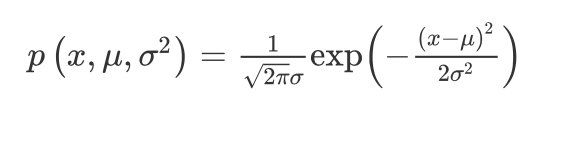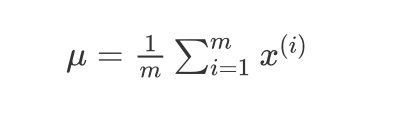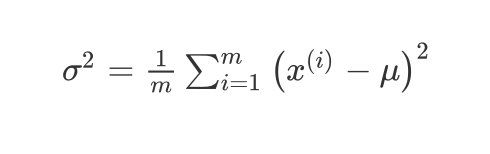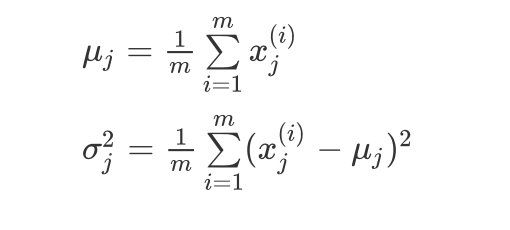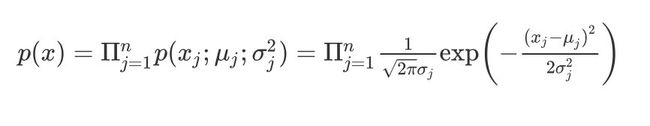吴恩达机器学习-10-异常检测
公众号:尤而小屋
作者:Peter
编辑:Peter
吴恩达机器学习-10-异常检测
“黑中有白,白中有黑,没有绝对的白,也没有绝对的黑,黑可衬白,白可映黑。万物皆可转换”
在本周中主要讲解了机器学习中的异常检测问题,主要包含:
- 问题产生
- 高斯分布
- 算法使用场景
- 八种无监督异常检测技术
- 异常检测和监督学习对比
- 特征选择
异常检测Novelty Detection
异常是相对于其他观测数据而言有明显偏离的,以至于怀疑它与正常点不属于同一个数据分布。
异常检测是一种用于识别不符合预期行为的异常模式的技术,又称之为异常值检测。
在商业中也有许多应用,如网络入侵检测(识别可能发出黑客攻击的网络流量中的特殊模式)、系统健康性监测、信用卡交易欺诈检测、设备故障检测、风险识别等
问题动机
异常检测主要是运用于非监督学习的算法。问题的引出:通过飞机的检测开始。
检测飞机的引擎制造商生产了一批飞机引擎,测试了其中的一些特征变量,比如引擎运转时产生的热量,或者引擎的振动等。
假设有m个引擎,数据如下:
x ( 1 ) , x ( 2 ) , … , x ( m ) x^{(1)},x^{(2)},…,x^{(m)} x(1),x(2),…,x(m)
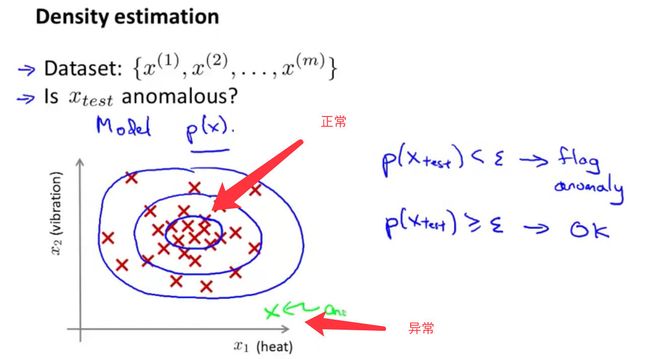
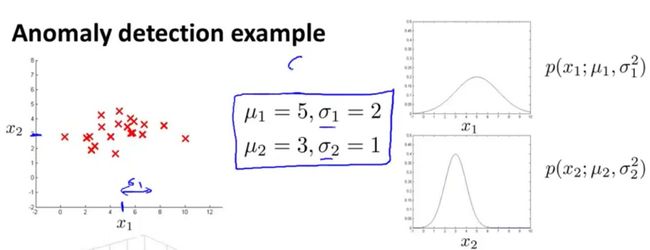
绘制出如下图表:
对于给定的数据集,需要检测 x t e s t x_{test} xtest是不是异常的,即这个测试数据不属于这组数据的几率是多少。
从上图看出,在蓝色圈内属于该组的概率高,越是偏远的概率,属于该组的可能性就越低。
i f p ( x ) { < ε a n o m a l y = ε n o r m a l if \quad p(x) \begin{cases} < \varepsilon & anomaly \\=\varepsilon & normal \end{cases} ifp(x){ <ε=εanomalynormal
另外两个异常检测的应用例子是
- 识别欺骗行为,通过用户多久登陆一次、访问过的页面、发布帖子的数量等建立模型,通过模型来识别那些不符合该模型的用户。
- 检测数据中心的使用情况:内存使用、被访问的磁盘数量、CPU负载等
高斯分布
高斯分布也叫正态分布。分布满足:
x ∼ N ( μ , σ 2 ) x \sim N\left(\mu, \sigma^{2}\right) x∼N(μ,σ2)
概率密度函数为:
p ( x , μ , σ 2 ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p\left(x, \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) p(x,μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
均值 μ \mu μ为:
μ = 1 m ∑ i = 1 m x ( i ) \mu=\frac{1}{m} \sum_{i=1}^{m} x^{(i)} μ=m1i=1∑mx(i)
方差 σ 2 \sigma^2 σ2为 :
σ 2 = 1 m ∑ i = 1 m ( x ( i ) − μ ) 2 \sigma^{2}=\frac{1}{m} \sum_{i=1}^{m}\left(x^{(i)}-\mu\right)^{2} σ2=m1i=1∑m(x(i)−μ)2
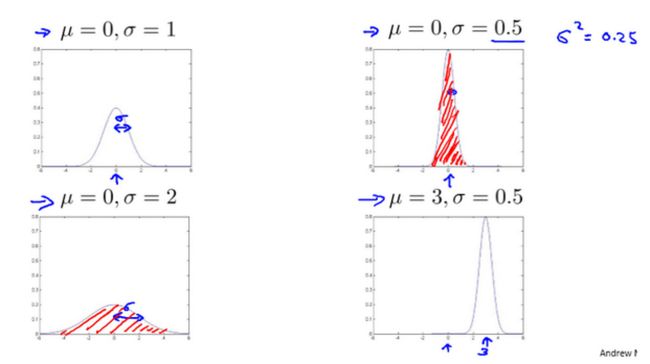
高斯分布的样例为
当均值 μ \mu μ相同的时候
- 方差的平方越大,图形是矮胖的
- 方差的平方越小,图形是瘦高型的
使用场景
异常检测算法的使用场景一般是三种:
- 在做特征工程的时候需要对异常的数据做过滤,防止对归一化等处理的结果产生影响
- 对没有标记输出的特征数据做筛选,找出异常的数据
- 对有标记输出的特征数据做二分类时,由于某些类别的训练样本非常少,类别严重不平衡,此时也可以考虑用非监督的异常点检测算法来做
算法
算法的具体过程是
-
对于给定的数据集:
x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m)
计算每个特征的 μ ; σ 2 \mu;\sigma^2 μ;σ2 的估计值
-
两个参数的估计值为:
μ j = 1 m ∑ i = 1 m x j ( i ) \mu_j=\frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)} μj=m1i=1∑mxj(i)
σ j 2 = 1 m ∑ i = 1 m ( x j ( i ) − μ j ) 2 \sigma_j^2=\frac{1}{m}\sum\limits_{i=1}^m(x_j^{(i)}-\mu_j)^2 σj2=m1i=1∑m(xj(i)−μj)2
- 利用高斯分布进行计算 p ( x ) p(x) p(x)
p ( x ) = Π j = 1 n p ( x j ; μ j ; σ j 2 ) = Π j = 1 n 1 2 π σ j exp ( − ( x j − μ j ) 2 2 σ j 2 ) p(x)=\Pi^n_{j=1}p(x_j;\mu_j;\sigma^2_j)=\Pi^n_{j=1}\frac{1}{\sqrt{2 \pi} \sigma_j} \exp \left(-\frac{(x_j-\mu_j)^{2}}{2 \sigma^{2}_j}\right) p(x)=Πj=1np(xj;μj;σj2)=Πj=1n2πσj1exp(−2σj2(xj−μj)2)
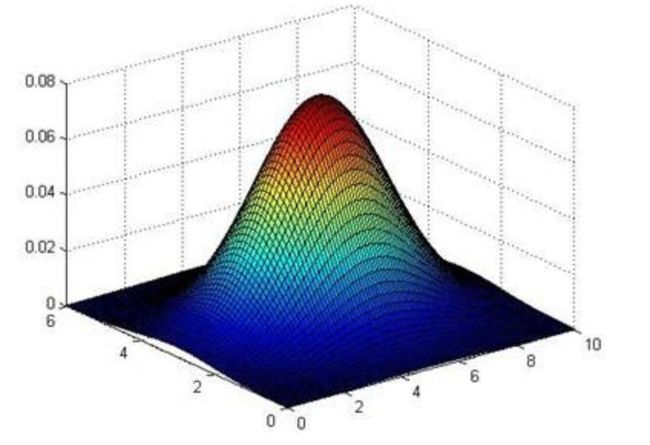
- 两个特征的训练集及特征非部分情况
- 三维图表示的是密度函数, z z z轴为根据两个特征的值估计的 p ( x ) p(x) p(x)的值
当 p ( x ) > ε p(x) > \varepsilon p(x)>ε时候,预测是正常数据, 否则为异常
异常算法的设计
当我们开发一个异常检测系统时,从带标记(异常或正常)的数据着手
- 从其中选择一部分正常数据用于构建训练集
- 然后用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试集。
八种无监督异常检测技术
- 基于统计的异常检测技术
MA滑动平均法3—Sigma(拉依达准则)
- 基于密度的异常检测
- 基于聚类的异常检测
- 基于``K-Means`聚类的异常检测
One Class SVM的异常检测Isolation Forest的异常检测PCA+MD的异常检测AutoEncoder异常检测
异常检测和监督学习对比
异常检测中采用的也是带标记的数据,和监督学习类似。二者对比为:
| 异常检测 | 监督学习 |
|---|---|
| 非常少量的正向类(异常数据 y = 1 y=1 y=1), 大量的负向类( y = 0 y=0 y=0) | 同时有大量的正向类和负向类 |
| 许多不同种类的异常,非常难。根据非常 少量的正向类数据来训练算法。 | 有足够多的正向类实例,足够用于训练 算法,未来遇到的正向类实例可能与训练集中的非常近似。 |
| 未来遇到的异常可能与已掌握的异常、非常的不同。 | |
| 例如: 欺诈行为检测 生产(例如飞机引擎)检测数据中心的计算机运行状况 | 例如:邮件过滤器 天气预报 肿瘤分类 |
当正样本的数量很少,甚至有时候是0,即出现了太多没见过的不同的异常类型,对于这些问题,通常应该使用的算法就是异常检测算法。
特征选择
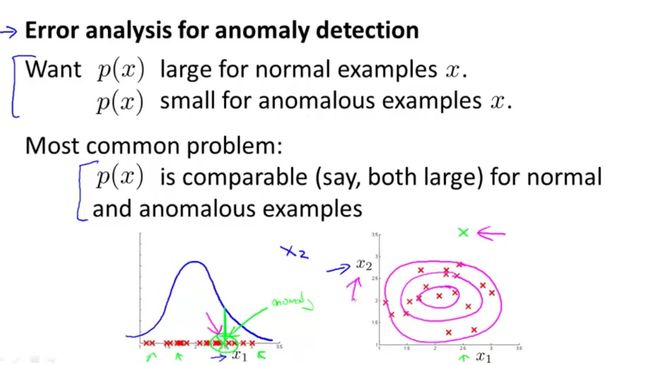
异常检测算法是基于高斯分布的。当然不满足高斯分布也能处理,但是最好转成高斯分布。误差分析是特征选择中很重要的点。
有些异常数据可能出现较高的 p ( x ) p(x) p(x)的值,被算法当做是正常数据。通过误差分析,增加新的特征得到新的算法,帮助我们更好地进行异常检测。
新特征获取:通过原有特征进行组合,得到新的特征
参考资料
- 李航-统计学习方法
- [八种无监督异常检测技术](