【MATLAB】画图、分支、循环、函数、复数、字符

四．MATLAB基础——画图

1. 标题：title('ploy of x and y');

坐标轴：xlabel('x');ylabel('y');

打开网格：grid on;

2.联合作图：plot(x,y1,x,y2);

3. MATLAB 允许程序员选择轨迹的颜色,轨迹的形式,和符号的类型.在 X,Y 向量参数后带有这些属性的字符串的 plot 函数,可以选择这些细节.这些属性字符串包括三个方面,第一方面指定轨迹的颜色,第二方面指定符号的类型,第三方面指定线的类型.

颜色		标记（符号）类型		线型标记类型
y	黄色	.	点	-	实线
m	品红色	o	圈	:	点线
c	青绿色	x	×号	-.	画点线
r	红色	s	正方形	--	虚线
g	绿色	d	菱形		无
b	蓝色	v	倒三角
w	白色	^	正三角
k	黑色	>、<	三角(向右)、 (向左)
		p	五角星
		h	六线形

4.使用legend制作图例：legend('f(x)','d/dx f(x)')

legend('string1','string2',...,pos)，其中 string1,string2 等等是与轨迹标签名，而 pos 是一个整数，用来指定图例的位置：

0	‘Best’	自动寻找最佳位置，至少不与数据冲突
1	‘NorthEast’	在图象的右上角
2	‘NorthWest’	在图象的左上角
3	‘SouthWest’	在图象的左下角
4	‘SouthEast’	在图象的右下角
-1	'NorthEastOutside'	在图象的右边

5. 打印数据既可以用对数尺度，也可以用线性尺度。在 x,y 轴上使用这两种尺度的一种或两种可以组合形成 4 种不同的坐标系。每一种组合者有一个特定的函数。

1.plot 函数的 x,y 均用线性尺度

2.semilog 函数 x 轴用对数尺度， y 轴将用线性尺度

3.semiloge 函数 x 轴用线性尺度， y 轴用对数尺度

4.loglog 函数两坐标轴将会都用对数尺度。

这四个函数在意义上是等价的，只是坐标轴的类型不同。

6.控制画图的上下限：

v=axis	返回一个 4 元素行向量[xmin xmax ymin ymax]，其中 xmin xmax ymin ymax 代表 x， y 轴的上下限
axis([xmin xmax ymin ymax])	xmin xmax 设定横轴的下限及上限， ymin ymax 设定纵轴的下限及上限
axis equal	将横轴纵轴的尺度比例设成相同值
axis square	横轴及纵轴比例是 1:1
axis normal	以预设值画纵轴及横轴
axis off	将纵轴及横轴取消
axis on	打开所有的轴标签，核对符号，背景(默认情形)

7.同一坐标系画多个图像：
当 hold on 命令执行后，所有的新的图象都会叠加在原来存在的图象。 hold off 命令可恢复默认情况，用新的图象来替代原来的图象。

8.创建多个图像：
“figure(n)”， 其中 n 代表图象数。当这个函数被执行后，图 n 将会变为当前图象，执行所有的画图命令。gcf 函数用于当于返回当前图象数。当你需要知道当前图象数时，你就把这个函数写入M 文件中。

figure(1);

x=x:0.05:2;

y1=exp(x);

plot(x,y1);

figure(2);

y2=exp(-x);

plot(x,y2);

 

9.子图像：

subplot(m,n,p)，这个命令在当前图象窗口创建了 m×n 个子图象，按 m 行， n 列排列，并选择子图象 p来接受当前所有画图命令。

figure(1);

subplot(2,1,1);

x=x:0.05:2;

y1=exp(x);

plot(x,y1);

title('subplot1');

subplot(2,1,2);

y2=exp(-x);

plot(x,y2);

title('subplot2');

10.对画线的增强控制：

LineWidth：用来指定线的宽度

MarkerEdgeColor：用来指定标识表面的颜色

MarkerFaceColor：填充标识的颜色

MarkerSize：指定标识的大小

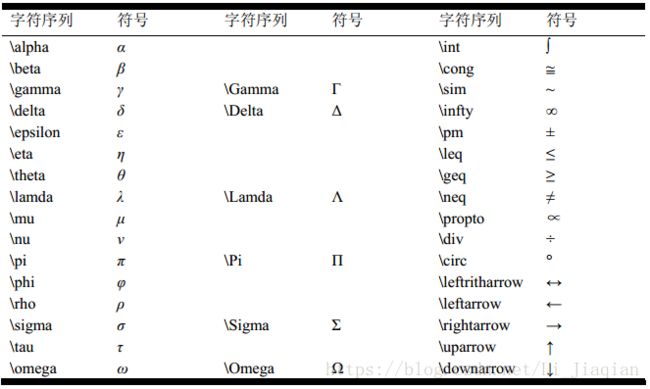
11.文本字符串的高级控制：
\bf 黑体

\it 斜体

\rm 恢复正常字体

\fontname 字体的名字

\fontsize 字体的大小

_{xxx} xxx 做为某字符的上标

^{xxx} xxx 做为某字符的下标

如果一个 modifier 后在跟着一个{}，只有{}中的文本起作用。如果要打印转义符\， {， }， _，或^就必须在前面加上一个反斜杠。

12.极坐标图像polar：
g=0.5;

theta=0:pi/20:2*pi;

func=2*g*(1+cos(theta));

polar(theta,func);

五．MATLAB基础——分支语句

1.关系运算符：

=	等于
~=	不等于
>	大于
>=	大于等于
<	小于
<=	小于等于

2.round off错误：

用这两个运算符比较两个字符串他是安全的， 不会出现错误。但对两个数字数据的比较，将可能产生异想不到的错误。两个理论上相等的数不能有一丝一毫的差别，而在计算机计算的过程中出现了近似的现象，从而可能在判断相等与不相等的过程中产生错误，这种错误叫做 round off 错误。我们可以通过检测两数之间在一定的范围内是不是近似相等， 在这个精确范围内可能会产生 round off 错误。例如测试
>> abs(a - b) < 1.0E-14
ans =1
将会产生正确的结果，不管在 a 与 b 的计算中产不产生的 round off 错误。

3.逻辑运算符：

&	与
|	或
xor	与或
~	非

4.逻辑函数：

ischar(a)	a是字符数组	1
isempty(a)	a是空数组	1
isinf(a)	a是无穷大	1
isnan(a)	a不是一个数	1
isnumeric(a)	a是一个数值数组	1

5.if结构：

if …

       … …

elseif …

       … …

else

       … …

end

 

利用分支语句，求解一元二次方程：

disp('this program solves for the roots of a quadratic');

a=input('A=');

b=input('B=');

c=input('C=');

derta=b^2-4*a*c;

if derta>0

    x1=(-b+sqrt(derta))/(2*a);

    x2=(-b-sqrt(derta))/(2*a);

    fprintf('x1=%f,x2=%f\n',x1,x2);

elseif derta==0

    x1=-b/(2*a);

    fprintf('x1=x2=%f\n',x1);

else

    shibu=-b/(2*a);

    xubu=sqrt(abs(derta))/(2*a);

    fprintf('x1=%f+%fi,x2=%f-%fi\n',shibu,xubu,shibu,xubu);

end

 

6.switch结构：
switch 结构是另一种形式的选择结构。程序员可以根据一个单精度整形数，字符或逻辑

表达式的值来选择执行特定的代码语句块。

value=input('your number:');

switch(value)

    case{1,3,5,7,9},

        disp('odd');

    case{2,4,6,8},

        disp('even');

    case 10,

        disp('ten');

    otherwise,

        disp('out of range.')

end

 

7.try/catch结构：

如果一个错误发生在这个结构的 try 语句块中，那么程序将会执行 catch 语句块，程序

将不会中断。它将帮助程序员控制程序中的错误，而不用使程序中断。

六．循环结构

1.while：

while …

       … …

end

 

2.for:

for ii=1:2:10

for ii=[1 2 3]

for ii=[1 2 3;4 5 6]——(ii=[1;4],[2;5],[3;6])

 

3.那种既可以用向量可以解决的问题，也可以用循环解决的问题，最好用向量解决，这是因为向量执行的速度快。

tic;

s1=[];

for i=1:10000

    s1(i)=i^2;

end

toc

 

tic;

s2=zeros(1,10000);

for i=1:10000

    s2(i)=i^2;

end

toc

 

tic;

s3=[];

for i=1:10000

    s3=i.^2;

end

toc

 

4. break 语句可以中止循环的执行和跳到 end 后面的第一句执行，而 continue 只中止本次循环，然后返回循环的顶部。

七．自定义函数

1. 在一个函数中的初始注释行有特定的目的。在 function 语句的第一个行注释被称为 H1注释行。它应当是对本函数功能的总结。这一行的重要性在于，通过 lookfor 命令它能被搜索到并显示出来。从 H1 注释行到第一个空行或第一个可执行性语句可以通过 help 命令或帮助窗口搜索到。它们则应包含如何使用这个函数的简单总结。

2.调用一个函数时，将实参复制生成副本，对副本进行操作，不会影响原实参的数值。

3.排序：内置于 MATLAB 的 sort 和 sortrows 函数是非常高效的，在实际工作中我们应当应用这些函数。

4.选择性参数：支持多个输入，多个输出

function [mag,angle]=polar_value(x,y)

%将直角坐标(x,y)转化为相应的极坐标

%若输入参数只有一个，则该函数假设y=0

%若输出参数只有一个，则只返回模

msg=nargchk(1,2,nargin);

%若被调用时，参数个数不在[1,2]则返回错误信息

error(msg);

if nargin<2

    y=0;

end

%输入参数只有一个，假设y=0

if x==0 & y==0

    msg='Both x and y is zero:angle is meaningless.';

    warning(msg);

end

%x=0,y=0,极坐标的角度没有意义

mag=sqrt(x.^2+y.^2);

if nargout==2

    angle=atan2(y,x)*180/pi;

end

%输出参数有两个，求出极坐标的角度值

 

5. MATLAB 函数与每一个参数或基本工作区通过全局内存交换数据。全局内存是指内存的一种特殊类型，它能够被所有的工作区访问。如果一个变量在函数中被声明全局变量，那么它将占用的是全局内存，而不是本地工作区。如果相同的变量在另一个函数中被声明为全局变量，那么这个变量所占有内存区域就是第一个函数中的相同变量。声明有全局变量的脚本文件或函数将有办法访问相同的值， 所以全局变量为函数之间分享数据提供了一个方法。global v1,v2,v3…

6.简单的随机数发生器：
ni+1 = mod(8121ni + 28411, 134456)

假设 ni 为非负整数，那么由于求余函数的关系， ni+1 只能在 0 到 13445 之间的整数中进行取值。 重复以上过程， 得到的结果永远是在区间[0, 134455]中。 如果我们事先不知道 8121，28411 和 134456 这三个数你很可能猜测这个顺序是由 n 值产生的。进一步说，它说明，所有在 0 到 13445 之间的整数出现的次序是等可能性。

seed.m:

function seed(new_seed)

global ISEED

msg=nargchk(1,1,nargin);

error(msg);

new_seed=round(new_seed);

ISEED=abs(new_seed);

 

random.m:

function ran=random0(n,m)

global ISEED

msg=nargchk(1,2,nargin);

error(msg);

if nargin<2

    m=n;

end

ran=zeros(n,m);

for ii=1:n

    for jj=1:m

        ISEED=mod(8121*ISEED+28411,134456);

        ran(ii,jj)=ISEED/134456;

    end

end

 

>> arr=random0(1,20000);

>> mean(arr)

 

ans =

 

    0.5019

 

>> std(arr)

 

ans =

 

    0.2881

 

>> hist(arr,10);

>> title('\bfHistorygram of the output of random0');

>> xlabel('bin')

>> ylabel('count')

https://blog.csdn.net/qq_38237482/article/details/78608521

7.在两次函数调用之间有持久内存保存本地数据：persistent v1,v2,v3…

例.输入数据获取均值与方差

runstats.m:

function [avg,std]=runstats(x)

persistent n

persistent sum_x1

persistent sum_x2

msg=nargchk(1,1,nargin);

error(msg);

if x=='reset'

    n=0;

    sum_x1=0;

    sum_x2=0;

else

    n=n+1;

    sum_x1=sum_x1+x;

    sum_x2=sum_x2+x^2;

end

if n==0

    avg=0;

    std=0;

elseif n==1

    avg=sum_x1;

    std=0;

else

    avg=sum_x1/n;

    std=sqrt((n*sum_x2-sum_x1^2)/(n*(n-1)));

end

 

test_runstats:
[avg std]=runstats('reset');

nvals=input('enter number of values in data set:');

for ii=1:nvals

    string=['enter value ',int2str(ii),':'];

    x=input(string);

    [avg std]=runstats(x);

    fprintf('Average=%8.4f;Std dev=%8.4f\n',avg,std);

end

8.函数的函数：
fzero(‘func’,[a,b])确定函数在[a,b]何时为零，返回使函数为零的自变量的值。fzero('cos',[0 pi])

eval(string)求string表示的函数的值。x=eval(‘sin(pi/4)’)

feval(func,value)求函数在value下的结果。x=feval(‘sin’,pi/4)

fminbnd	求函数的极小值，这函数只有一个自变量
fzero	找出函数为 0 时的自变量的值
quad	积分quad(‘sin’,0,pi)=2
ezplot	简单易用的函数画图
fplot	通过函数名画出这个函数的图象fplot(sin)

八．复数数据、字符数据和附加画图类型

1. 关系运算符>， <， <=或>=只比较复数的实部，而不是它们的模。如果你要用这些关系运算符对一复数进行运算，比较两复数的模将更加常见。

2. 许多的数函数都可以对复数进行运算。这些函数包括指数函数，对数函数，三角函数，还有平方根函数。函数 sin， cos， log， sqrt 等既能对复数数据进行运算，又能对实数据进行运算。

conj(c)	计算 c 的共轭复数。如果 c=a+bi，那么 conj(c)=a-bi。
real(c)	返回复数 c 的实部
imag(c)	返回复数 c 的虚部
isreal(c)	如果数组 c 中没有一个元素有虚部，函数 isreal(c)将返回 1。所以如果一个数组 c 是复数组成，那么~isreal(c)将返回 1。
abs(c)	返回复数 c 模
angle(c)	返回复数 c 的幅角，等价于 atan2(imag(c)， real(c))

3.虚数画图：

t=0:pi/20:4*pi;

y=exp(-0.2*t).*(cos(t)+i.*sin(t));

%(1)

% plot(t,y);

%(2)

% plot(t,real(y),'b-');

% hold on;

% plot(t,imag(y),'r-');

%(3)

plot(y,'b-');

% title('\bfPlot of Complex Function vs Time');

% xlabel('\bf\itt');

% ylabel('\bf\ity(t)');

% legend('real','imaginary');

%hold off;

4.double：字符->asci，char：ascii->字符

str='This is a test'

x=double(str)

y=char(x)

5.使用char创建二维字符数组，自动寻找最长的字符串，使用deblank去掉由于匹配最长字符串而多出的空格，blanks(n)创建由n个空格组成的字符串。

name=char('hello','whorldddddd')

line0=name(1,:)

line1=deblank(line0)

size(line0)

size(line1)

6.字符串连接：strcat水平拼接，删去字符串末尾的空格，strvcat垂直拼接，拼成二维字符串数组，自动补全末尾空格，与最长字符串对齐。

result=strcat('string   1   ','string2')

result=strvcat('Longstring1    ','string2')

7.字符串比较：MATLAB内建函数只能判断字符串是否等价，不能比较整个字符串的大小。

strcmp	判断两字符串是否等价，等价为1，不等价为0
strcmpi	忽略大小写判断两字符串是否等价
strncmp(s1,s2,n)	判断两字符串前 n 个字符是否等价
strncmpi	忽略大小写判断两字符串前 n 个字符是否等价

8.字符比较：利用 MATLAB 关系运算符对字符数组中的每一个元素进行检测，看是否相同，

但是我们要保证它们的维数是相同的， 或其中一个是标量。

str='Room 23a';

isletter(str)%alpha

isspace(str)

isstrprop(str,'alpha')%alpha

isstrprop(str,'alphanum')%number or alpha

isstrprop(str,'cntrl')%char(1:20)

isstrprop(str,'digit')%number

9.字符串操作：

findstr(str,str2)	返回str2在str1中所有的出现位置，从1开始
strmatch(str,array)	返回二维数组array开头为str的行号
strrep(str1,str2,str3)	找到str1中所有的str2，用str3替换
strjust(str)	以最长字符串长度，去掉末尾空格，右对齐
[token,remainder]=strtok(str1,str2)	返回str1中出现在str2之前的字符，给token，剩下的给remainder，可用其把句子转化为单词
upper、lower
eval(str)、value=sscanf(string,format)	字符串->数字
int2str	转化为整数字符串
num2str(pi,n),num2str(pi,’%10.5e’)	保留n位数字
hex2num，hex2dec， bin2dec， dec2bin， base2dec
mat2str	数组->字符串
lenth(str)	返回str大小

10.ndims(c):返回数组维数，size(c):返回每维数组大小

11.二维作图：

bar(x, y)	这个函数用于创建一个水平的条形图， x代表第一个 X 轴的取值， y 代表对应于 Y 的取值
barh(x, y)	这个函数用于创建一个竖直的条形图， x 代表第一个 X 轴的取值， y 代表对应于 Y 的取值
compass(x, y)	这个函数用于创建一个极坐标图，它的每一个值都用箭头表示，从原点指向（x， y），注意：（x， y）是直角坐标系中的坐标。
pie(x) pie(x, explode)	这个函数用来创建一个饼状图，x代表占总数的百分数。explode 用来判断是否还有剩余的百分数x=[1,2,3,4];explode=[1 0 0 0];pie(x,explode)
stairs(x, y)	用来创建一个阶梯图，每一个阶梯的中心为点(x, y)
stem(x, y)	这个函数可以创建一个针头图，它的取值为(x,y)