java数据结构-快速了解链表的增删查改
文章目录
- 一、链表的概念和结构
-
- 1.链表的概念
- 2.链表的分类
- 二、单向不带头非循环链表
-
- 1.创建节点类型
- 2.头插法
- 3.尾插法
- 4.获取链表长度
- 5.任意位置插入
- 6.查找关键字
- 7.删除第一次出现值为key的节点
- 8.删除所有值为key的节点
- 9.遍历打印链表
- 10.置空链表
- 二、双向不带头非循环链表
-
- 1.创建节点类型
- 2.头插法
- 3.尾插法
- 4.获取链表长度
- 5.任意位置插入
- 6.查找关键字
- 7.删除第一次出现的关键字key的节点
- 8.删除所有值为key的节点
- 9.遍历打印链表
- 10.置空链表
- 总结
一、链表的概念和结构
1.链表的概念
简单来说链表是物理上不一定连续,但是逻辑上一定连续的一种数据结构
2.链表的分类
实际中链表的结构非常多样,以下情况组合起来就有8种链表结构. 单向和双向,带头和不带头,循环和非循环。排列组合和会有8种。
但我这只是实现两种比较难的链表,理解之后其它6种就比较简单了
1.单向不带头非循环链表
2.双向不带头非循环链表
二、单向不带头非循环链表
1.创建节点类型
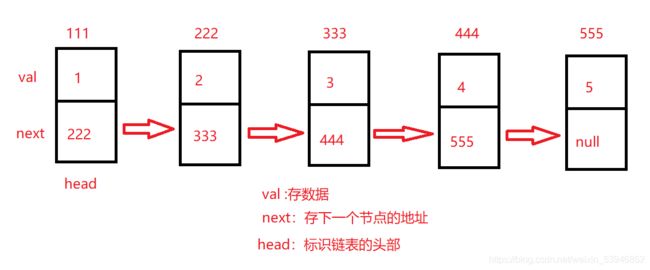
我们创建了一个 ListNode 类为节点类型,里面有两个成员变量,val用来存储数值,next来存储下一个节点的地址。
还有一个带一个参数的构造方法在实例化对象的同时给val赋值,因为我们不知道下一个节点的地址所以next是默认值一个null
class ListNode {
public int val;//数值
public ListNode next;//下一个节点的地址
public ListNode(int val) {
this.val = val;
}
}
我们在 MyLinkedList 里创建一个head变量来标识链表的头部,接着就是实现单链表的增删查改了
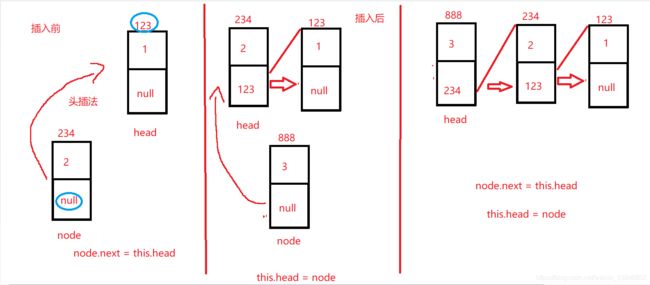
2.头插法
//头插法
public void addFirst(int data) {
ListNode node = new ListNode(data);
node.next = this.head;
this.head = node;
}
3.尾插法
尾插法首先要考虑是不是第一次插入,如果是的话直接把head指向node就好了,如果不是第一次插入,则需要定义一个cur来找尾巴节点,把尾巴节点的next值改成node就好了。因为如果不用尾巴节点的话,head就无法标识到头部了
//尾插法
public void addLast(int data) {
ListNode node = new ListNode(data);
ListNode cur = this.head;
//第一次插入
if(this.head == null) {
this.head = node;
}else{
while (cur.next != null) {
cur = cur.next;
}
cur.next = node;
}
}
4.获取链表长度
定义一个计数器count,当cur遍历完链表的时候直接返回count就好
//得到单链表的长度
public int size() {
int count = 0;
ListNode cur = this.head;
while (cur != null) {
cur = cur.next;
count++;
}
return count;
}
5.任意位置插入
我们假设链表的头是从0位置开始的,任意位置插入需要考虑几点
1.位置的合法性,如果位置小于0,或者大于链表长度则位置不合法
2.如果要插入的是0位置直接使用头插法
3.如果插入的位置等于链表长度则使用尾插法,因为我们这链表是从0开始的
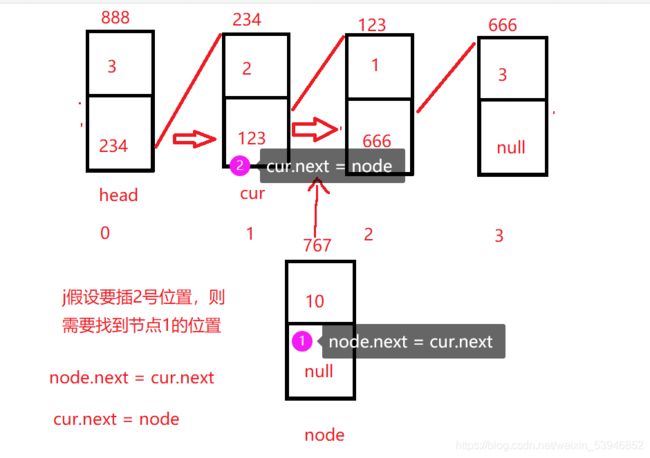
4.最关键的就是从中间任意位置插入 要从中间位置插入,就需要找到要插入位置的前一个节点的位置。再插入到它们中间。
/**
* 让 cur 向后走 index - 1 步
* @param index
* @return
*/
public ListNode findIndexSubOne(int index) {
int count = 0;
ListNode cur = this.head;
while (count != index-1) {
cur = cur.next;
count++;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data) {
//判断合法性
if(index < 0 || index > size()) {
System.out.println("index位置不合法");
return;
}
//头插法
if(index == 0) {
this.addFirst(data);
return;
}
//尾插法
if(index == size()) {
this.addLast(data);
return;
}
//找前驱,cur指向的是 index 的前一个节点
ListNode cur = findIndexSubOne(index);
ListNode node = new ListNode(data);
node.next = cur.next;
cur.next = node;
}
6.查找关键字
当我们要查找链表中是否有某一个关键字时,只需要定义一个cur从头开始遍历即可
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
7.删除第一次出现值为key的节点
这个思路其实也很简单,考虑到两种情况即可
1.如果要删除的是头节点只需要把头节点指向它的向一个节点即可
2.还有一种则是不存在key的情况,所以这里写了一个方法来判读key是否存在,如果存在则返回key的前一个节点的位置
3.存在则把要删除的节点的前驱的next改成它的next即可
/**
* 找要删除 key 的前一个节点
* @return
*/
public ListNode searchPrev(int key) {
ListNode prev = this.head;
while (prev.next != null) {
if (prev.next.val == key) {
return prev;
}
prev = prev.next;
}
return null;
}
//删除第一次出现关键字为key的节点
public void remove(int key) {
if(this.head.val == key) {
this.head = this.head.next;
return;
}
//找 key 的前驱节点
ListNode prev = searchPrev(key);
if(prev == null) {
System.out.println("没有key这个关键字");
return;
}
//删除
ListNode delete = prev.next;
prev.next = delete.next;
}
8.删除所有值为key的节点
假设要删除的是3,思路:
定义两个节点点类型的变量,prev指向head,cur指向head的下一个节点。
如果判断cur的val值是要删除的值,如果是则直接跳过这个节点 如果不是则让prev和cur往后走,直到整个链表遍历完。
到最后会发现头节点并没有遍历到,循环结束后则需要判读头节点是不是要删除的节点
记住一定要边画图边写代码!
//删除所有值为key的节点
public void removeAllKey(int key) {
ListNode prev = this.head;
ListNode cur = this.head.next;
while (cur != null) {
if(cur.val == key) {
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;
cur = cur.next;
}
}
//判断第一个节点是否是要删除的节点
if(this.head.val == key) {
this.head = this.head.next;
}
}
9.遍历打印链表
定义一个cur直接遍历打印就好
//打印链表
public void display() {
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}
10.置空链表
置空链表只需要一个个置空即可,并不建议直接把头节点置空这种暴力做法
//置空链表
public void clear() {
ListNode cur = this.head;
//一个个制空
while (cur != null) {
ListNode curNext = cur.next;
cur.next = null;
cur = curNext;
}
this.head = null;
}
二、双向不带头非循环链表
双向链表和单向链表的最大的区别就是多了一个前驱节点prev,同样来实现双向链表的增删查改
public class TestLinkedList {
public ListNode head;
public ListNode last;
}
1.创建节点类型
同样先定义节点类型,比单向链表多了一个前驱节点而已。
class ListNode {
public int val;
public ListNode prev;
public ListNode next;
public ListNode (int val) {
this.val = val;
}
}
双向链表还定义了一个last来标识尾巴节点,而单链表只是标识了头节点。
2.头插法
因为这是双向链表,第一次插入要让head和last同时指向第一个节点。
如果不是第一次插入,则需要
1.把head的前驱节点改成node,
2.再把node的next改成head,
3.然后把头节点head再指向新的头节点node。
//头插法
public void addFirst(int data) {
ListNode node = new ListNode(data);
//第一次插入
if(this.head == null) {
this.head = node;
this.last = node;
}else {
head.prev = node;
node.next = this.head;
this.head = node;
}
}
3.尾插法
双向链表有一个last来标识尾巴节点,所以在尾插的时候不用再找尾巴节点了。和头插法类似
//尾插法
public void addLast(int data) {
ListNode node = new ListNode(data);
//第一次插入
if(this.head == null) {
this.head = node;
this.last = node;
}else {
this.last.next = node;
node.prev = this.last;
this.last = node;
}
}
4.获取链表长度
这个和单链表一样,直接定义个cur遍历
//得到链表的长度
public int size() {
ListNode cur = this.head;
int count = 0;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}
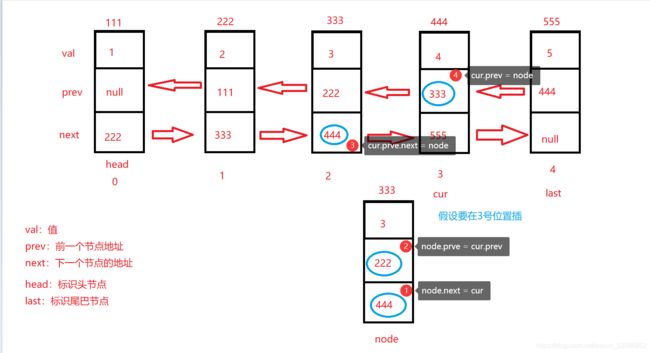
5.任意位置插入
任意位置插入也和单链表类似有三种情况。判断合法性和头插尾插就不多了主要还是在中间的随机插入,一定要注意修改的顺序!
要修改的地方一共有四个,一定要画图理解!
//找要插入的节点的位置
public ListNode searchIndex(int index) {
ListNode cur = this.head;
while (index != 0) {
cur = cur.next;
index--;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data) {
//判断index位置的合法性
if(index < 0 || index > this.size()) {
System.out.println("index的位置不合法");
return;
}
//头插法
if(index == 0) {
this.addFirst(data);
return;
}
//尾插法
if(index == this.size()) {
this.addLast(data);
return;
}
//中间插入
ListNode node = new ListNode(data);
ListNode cur = searchIndex(index);
node.next = cur;
node.prev = cur.prev;
cur.prev.next = node;
cur.prev = node;
}
6.查找关键字
这里和单链表一样,直接定义个cur遍历看看链表里有没有这个值即可
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
7.删除第一次出现的关键字key的节点
思路:遍历链表找第一次出现的节点,删完return。一共分三种情况
1.头节点是要删除的节点
2.尾巴节点是要删除的节点
3.中间的节点是要删除的节点
//删除第一次出现关键字为key的节点
public void remove(int key) {
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
//要删除的是头节点
if(this.head == cur) {
this.head = this.head.next;
this.head.prev = null;
}else {
//尾巴节点和中间的节点两种情况
cur.prev.next = cur.next;
if(this.last == cur) {
//删除尾巴节点
cur = cur.prev;
}else {
cur.next.prev = cur.prev;
}
}
//已经删完了
return;
}else {
cur = cur.next;
}
}
}
8.删除所有值为key的节点
思路和删除一个key类似,但需要注意两个点。
1.删完就不用return了,而是继续往后走,因为这里是删除所有为key需要把列表遍历完
2.还有就是要考虑当整个链表都是要删除的情况,if判断一下不然会发生空指针异常
//删除所有值为key的节点
public void removeAllKey(int key) {
ListNode cur = this.head;
while (cur != null) {
if(cur.val == key) {
//要删除的是头节点
if(this.head == cur) {
this.head = this.head.next;
//假设全部是要删除的节点
if(this.head != null) {
this.head.prev = null;
}else {
//防止最后一个节点不能被回收
this.last = null;
}
}else {
//尾巴节点和中间的节点两种情况
cur.prev.next = cur.next;
if(this.last == cur) {
//删除尾巴节点
cur = cur.prev;
}else {
cur.next.prev = cur.prev;
}
}
//走一步
cur = cur.next;
}else {
cur = cur.next;
}
}
}
9.遍历打印链表
//打印链表
public void display() {
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}
10.置空链表
遍历链表一个一个置为null,再把头节点和尾巴节点值为null。防止内存泄漏
//置空链表
public void clear() {
ListNode cur = this.head;
//一个一个置空
while (cur != null) {
ListNode curNext = cur.next;
cur.prev = null;
cur.next = null;
cur = curNext;
}
this.head = null;
this.last = null;
}
总结
1.这里实现了两种较难的链表:单向不带头非循环和双向不带头非循环
2.链表物理上不一定连续,但逻辑上一定连续。
3.增:链表插入一个元素只需要修改指向,所以时间复杂度为O(1)
4:删:链表删除元素,同样只需修改指向,时间复杂度为O(1)
5.查:链表如果需要查找一个元素需要遍历链表,所以时间复杂度为O(n)
6.改:链表要去找到要修改的元素,所以时间复杂度为O(n).
什么时候用链表?
如果是插入和删除比较频繁的时候,使用链表。注意:是不涉及到移动数据的情况!