A:牛牛与牛妹的RMQ | 2021牛客寒假算法基础集训营2

链接：https://ac.nowcoder.com/acm/contest/9982/A
时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K

题目描述

某天，牛妹来找牛牛学习RMQ算法(Range Minimum/Maximum Query),即区间最值查询。也就是给定一个数组区间[L,R]，查询该子区间的最大值。
假设子数组的两端点下标分别为L,R的话RMQ(L,R)就表示数组区间[L,R]的最大值。
因为牛妹学会了RMQ算法，所以牛牛准备和她玩个游戏验证她真的学会了。

牛牛有一个长度大小为n的全排列数组，即数组中的数字是1~n，且每个数字仅出现1次。
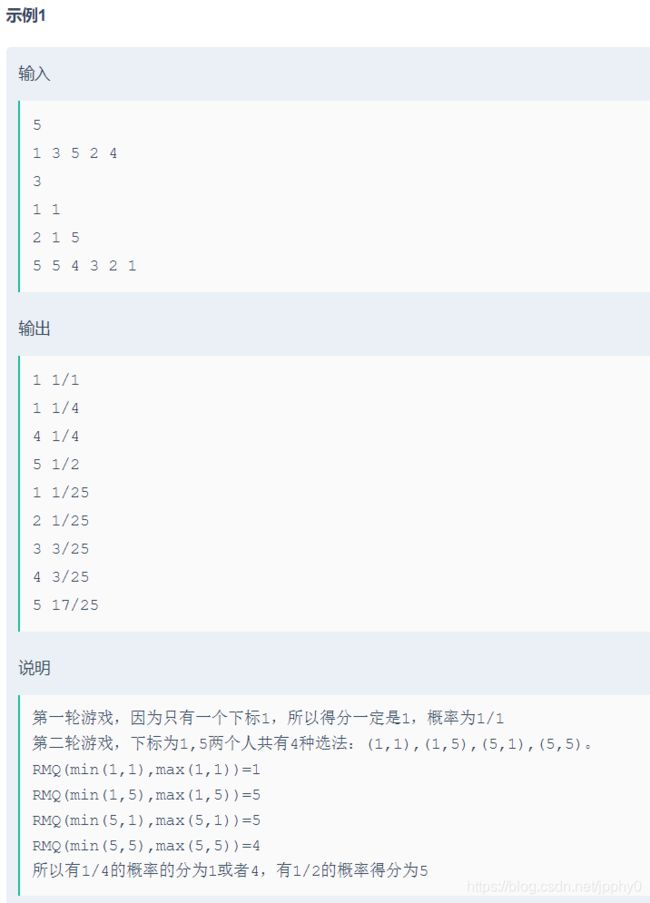
她们一共玩了m轮游戏，在每轮游戏中，牛牛都准备了k个不同的下标。
然后牛牛和牛妹各自随机选出一个下标，并且两人所选下标可以是相同的。
假设牛牛选出的下标为a，牛妹选出的下标为b的话，那么本轮游戏的得分就是RMQ(min(a,b),max(a,b))。

请你告诉牛牛，对于每轮游戏可能的得分都有哪几种情况，以及这些情况出现的概率各是多大？

分析

关键：如何遍历？

1. 遍历所有可能区间？超时不可行。（因为：p序列有k个元素，对这k个元素排序后，容易计算出这些元素可以产生k^2个可能区间）
2. 将k²个区间按得分进行分类，遍历所有的分类？最多2k-1个分类，可行且有效。设arr序列为（1，3， 5， 2， 4），则
   例1：如果p序列为（1，2，4，5），那么p序列的p1, p4对应arr序列的区间[1,5]，它的最大值为5(即arr3，下标i=3），因为i= 3在p序列中介于p2和p3间，借用下界的概念，最大值在p中的位置用p的下标3表示，因此有(3-1)(5-3) = 4个区间的得分为5（即arr3），出现5这个得分的次数为 2 (3-1)(5-3)=8次。到此，一个分类整体解决。
   例2：如果p序列为（1，3，4，5），那么p序列的p1, p4对应arr序列的区间[1,5]，它的最大值为5(即arr3，下标i=3），因为i= 3在p序列中等于p2，借用下界的概念，最大值在p中的位置用p的下标2表示，因此有(2-1+1)(5-3+1)-1 = 5个区间的得分为5（即arr3），出现5这个得分的次数为 2 ((2-1+1)(5-3+1)-1)=10次，此外还有[p2，p2]单独1次，共11次。
3. 问题的主要任务就是如何找出这些分类？或者说某个得分在哪些区间是有效的？可以尝试二分搜索 和 单调栈两种方法。

思路

1. st表存储下标，st表查询返回下标

2. 对p序列按升序排序
   二分处理

3. 按最大得分将整个区间二分，然后再对子区间二分处理，……，每个区间的最大值通过二分搜索确定
   单调栈

4. 对于一个最小区间的得分，它有可能向两侧扩展从而获得这个得分的有效区间。例如：当与它相邻的区间的得分比它的得分小，就可以扩展。遍历最小的区间可以扩展出所有区间。但扩展时，左侧边界的信息出现在已遍历的区间中，而右侧边界的信息将会出现在将要遍历的区间中，即：与过去相关，与未来相关。这时单调栈发挥作用，新区间的得分比栈顶区间得分小则入栈，且扩展新区间的左边界为栈顶区间的有边界；若新区间的得分比栈顶得分大，则弹出栈顶区间，且被弹出区间的有边界为新区间的左边界。被弹出的区间是左右边界都确定的，故这个区间对应的得分出现次数是可计算的。

5. 区间出现的次数存储在map中

6. L==R的区间（L，R）出现的1次单独处理

代码

使用单调栈

#include 
using namespace std;
#define MAXN 100010
#define LOGN 20
#define LL long long
struct sRngeInP{
     int L, R, u, a;} r[MAXN];
int n, a[MAXN], m, k, p[MAXN<<1], st[MAXN][LOGN];
void st_init(){
     
    int x, y;
    for(int i = 1; i <= n; i++) st[i][0] = i;
    for(int j = 1; (1<<j) <= n; j++){
     
        for(int i = 1; i-1+(1<<j) <= n; i++){
     
            x = st[i][j-1], y = st[i+(1<<(j-1))][j-1];
            st[i][j] = a[x] > a[y] ? x : y;
        }
    }
}
int st_query(int aL, int aR){
     
    int j = 0, x, y;
    while((1<<(j+1) < (aR - aL + 1))) j++;
    x = st[aL][j], y = st[aR - (1<<j) + 1][j];
    return a[x] > a[y] ? x : y;
}
LL gcd(LL x, LL y){
      return y ? gcd(y, x%y) : x;}
int main(){
     
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    n++,  a[n] = n;
    st_init();
    scanf("%d", &m);
    while(m--){
     
        stack<int> s;
        map<int, LL> res;
        scanf("%d", &k);
        LL tot = 1LL*k*k, tmp;        
        for(int i = 1; i <= k; i++) scanf("%d", p+i);
        k++, p[k] = n;
        sort(p+1, p+k+1, [](int x, int y){
     return x < y;});
        for(int i = 1; i < k; i++){
     
            r[i].L = i, r[i].R = i+1;
            r[i].a = st_query(p[i], p[i+1]);
            r[i].u = r[i].a == p[i] ? i : i+1;
            while(!s.empty() && a[r[i].a] > a[r[s.top()].a]){
     
                sRngeInP & rip = r[s.top()];
                s.pop();
                rip.R = r[i].L;
                if(s.empty()) r[i].L = rip.L;
                if(p[rip.u] == rip.a)
                    res[a[rip.a]] += 2*((rip.u-rip.L+1LL)*(rip.R-rip.u+1)-1);
                else
                    res[a[rip.a]] += 2*(rip.u-rip.L)*(rip.R-rip.u+1LL);
            }
            if(!s.empty() && a[r[i].a] == a[r[s.top()].a])
                r[s.top()].R = r[i].R;
            else{
     
                if(!s.empty() && a[r[i].a] < a[r[s.top()].a]){
     
                    r[i].L = r[s.top()].R;
                }
                s.push(i);
            }
        }
        for(int i = 1; i < k; i++) res[a[p[i]]]++;
        map<int, LL>::iterator it = res.begin();
        while(it != res.end()){
     
            tmp = gcd(it->second, tot);
            printf("%d %lld/%lld\n", it->first, it->second/tmp, tot/tmp);
            it++;
        }
    }
    return 0;
}

使用stl的lower_bound

#include 
using namespace std;
#define MAXN 100010
#define LOGN 20
#define LL long long
int n, a[MAXN], m, k, p[MAXN<<1], st[MAXN][LOGN];
LL tot, tmp;
map<int, LL> res;
queue<pair<int,int>> q;
void st_init(){
     
    int x, y;
    for(int i = 1; i <= n; i++) st[i][0] = i;
    for(int j = 1; (1<<j) <= n; j++){
     
        for(int i = 1; i-1+(1<<j) <= n; i++){
     
            x = st[i][j-1], y = st[i+(1<<(j-1))][j-1];
            st[i][j] = a[x] > a[y] ? x : y;
        }
    }
}
int st_query(int aL, int aR){
     
    int j = 0, x, y;
    while((1<<(j+1) < (aR - aL + 1))) j++;
    x = st[aL][j], y = st[aR - (1<<j) + 1][j];
    return a[x] > a[y] ? x : y;
}
LL gcd(LL x, LL y){
      return y?gcd(y, x%y):x;}
void bfs(){
     
    LL mx_a;
    int lower;
    while(!q.empty()){
     
        pair<int,int> pi = q.front();
        q.pop();
        int pL = pi.first, pR = pi.second;
        if(pL >= pR) continue;
        mx_a = st_query(p[pL], p[pR]);
        lower= lower_bound(p+pL, p+pR+1, mx_a, [pL](int const mid, LL const val){
     
            return a[st_query(p[pL], mid)] < a[val];
        }) - p;
        if(p[lower] != mx_a){
     
            q.push({
     pL, lower-1}), q.push({
     lower, pR});
            res[a[mx_a]] += 2*(lower- pL)*(pR - lower+ 1LL);
        }
        else{
     
            q.push({
     pL, lower-1}), q.push({
     lower+1, pR});
            res[a[mx_a]] += 2*((lower- pL + 1LL)*(pR - lower+ 1) - 1);
        }
    }
}
int main(){
     
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    st_init();
    scanf("%d", &m);
    while(m--){
     
        scanf("%d", &k);
        tot = k, tot *= k, res.clear();
        for(int i = 1; i <= k; i++) scanf("%d", p+i);
        sort(p+1, p+k+1, [](int x, int y){
     return x < y;});
        q.push({
     1, k});
        bfs();
        for(int i = 1; i <= k; i++) res[a[p[i]]]++;
        map<int, LL>::iterator it = res.begin();
        while(it != res.end()){
     
            tmp = gcd(it->second, tot);
            printf("%d %lld/%lld\n", it->first, it->second/tmp, tot/tmp);
            it++;
        }
    }
    return 0;
}

自定义二分

#include 
using namespace std;
#define MAXN 100010
#define LOGN 20
#define LL long long
int n, a[MAXN], m, k, p[MAXN<<1], st[MAXN][LOGN];
LL tot, gd;
map<int, LL> res;
queue<pair<int,int>> q;
void st_init(){
     
    int x, y;
    for(int i = 1; i <= n; i++) st[i][0] = i;
    for(int j = 1; (1<<j) <= n; j++){
     
        for(int i = 1; i-1+(1<<j) <= n; i++){
     
            x = st[i][j-1], y = st[i+(1<<(j-1))][j-1];
            st[i][j] = a[x] > a[y] ? x : y;
        }
    }
}
int st_query(int aL, int aR){
     
    int j = 0, x, y;
    while((1<<(j+1) < (aR - aL + 1))) j++;
    x = st[aL][j], y = st[aR - (1<<j) + 1][j];
    return a[x] > a[y] ? x : y;
}
int search_lower(int pL, int pR, int v){
     
    if(pL == pR) return pR;
    if(pL+1 == pR) return st_query(p[pL], p[pL]) == v ? pL : pR;
    int pM = (pL+pR)/2;
    if(st_query(p[pL], p[pM]) == st_query(p[pM], p[pR])) return pM;
    else if(st_query(p[pL], p[pM]) == v) return search_lower(pL, pM, v);
    else return search_lower(pM, pR, v);
}
void bfs(){
     
    LL mx_a, lower;
    while(!q.empty()){
     
        pair<int,int> &pi = q.front();
        q.pop();
        int pL = pi.first, pR = pi.second;
        if(pL >= pR) continue;
        mx_a = st_query(p[pL], p[pR]);
        lower = search_lower(pL, pR, mx_a);
        if(p[upper] != mx_a){
      // 区间最大值出现的位置不同
            q.push({
     pL, lower-1}), q.push({
     lower, pR}); // 两个子区间插入队列
            res[a[mx_a]] += 2*(lower - pL)*(pR - lower + 1); // 出现次数
        }
        else{
     
            q.push({
     pL, lower-1}), q.push({
     lower+1, pR}); // 两个子区间插入队列
            res[a[mx_a]] += 2*((lower - pL + 1)*(pR - lower + 1) - 1);// 出现次数
        }
    }
}
int main(){
     
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    st_init();
    scanf("%d", &m);
    while(m--){
     
        scanf("%d", &k);
        tot = k, tot *= k, res.clear();
        for(int i = 1; i <= k; i++) scanf("%d", p+i);
        sort(p+1, p+k+1, [](int x, int y){
     return x < y;});
        q.push({
     1, k}); // 整个区间插入队列
        bfs(); // 宽搜
        for(int i = 1; i <= k; i++) res[a[p[i]]]++; // L==R时出现1次
        map<int, LL>::iterator it = res.begin();
        while(it != res.end()){
     
            gd = __gcd(it->second, tot);
            printf("%d %lld/%lld\n", it->first, it->second/gd, tot/gd);
            it++;
        }
    }
    return 0;
}