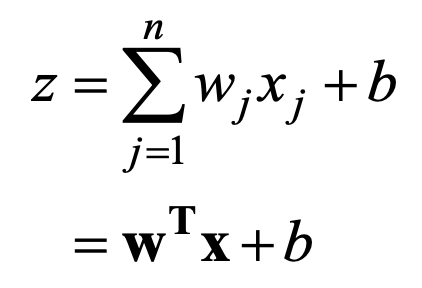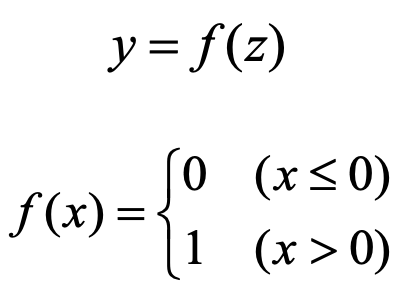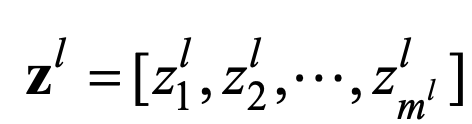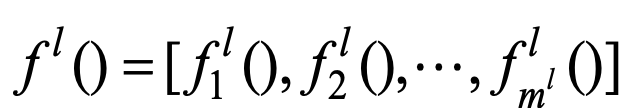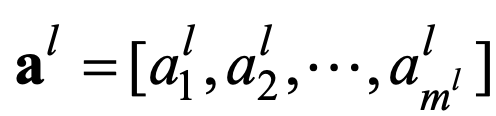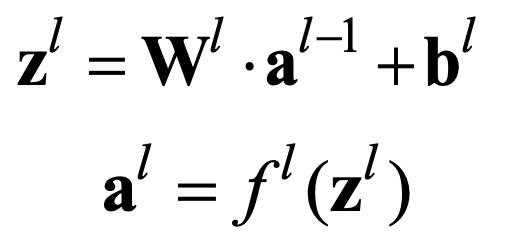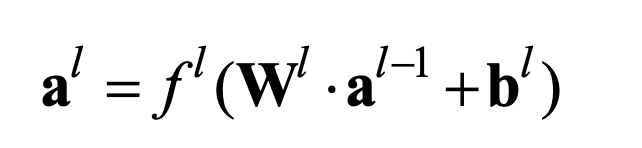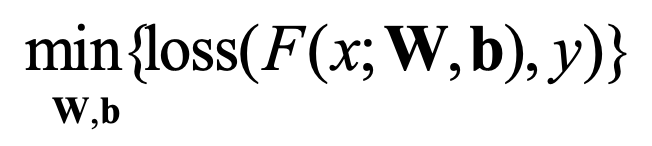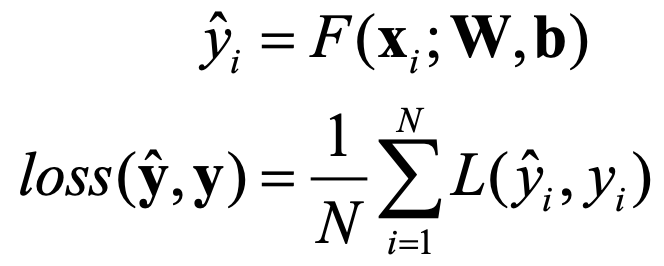从理论到实践，教你如何基于飞桨进行手写数字识别

本文节选自《深度学习导论与应用实践》

深度学习（Deep Learning）是近年来计算机业发展十分最为迅速的研究领域之一，并且在人工智能的很多子领域都取得了突破性的进展。特别是在2016年年初，由Deep Mind公司研发的AlphaGo以4:1的成绩击败了曾荣获18次世界冠军的围棋选手李世石(Lee Sedol)，AlphaGo声名鹊起，一时间“深度学习”的报道在媒体铺天盖地般的宣传下席卷了全球。

深度学习方法不仅在计算机领域大放异彩，也迅速在各领域攻城略地，在无人驾驶、自然语言处理，语音识别与金融大数据分析等方面都有广泛应用。接下来，我们将从神经网络的起源——感知机讲起，逐步介绍神经网络的运行机制与其核心算法，最后在深度学习理论基础之上，手把手教您如何使用飞桨（PaddlePaddle）深度学习框架解决手写数字识别问题，一步步走进深度学习精彩的世界。

01

神经网络的起源-感知机

感知机算法是由美国科学家Frank Rosenblatt在1957年提出，由此揭开了人工神经网络研究的序幕。

为何我们现在还要学习这一很久以前就有的算法呢？

 

因为感知机作为神经网络的起源的算法，学习感知机的构造也就是学习通往神经网络和深度学习的一种重要思想。

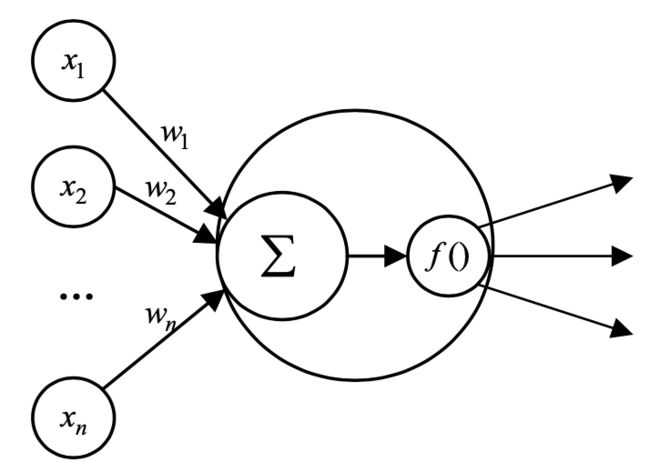
如上图所示，感知机接收多个输入信号，输出一个信号。X1,X2,X3为三个输入信号，y为输出信号，W1,W2,W3为感知机内部的参数，称为权重，图中的○通常称为“神经元”或者“节点”。输入信号与权重相乘后求和，与一个阈值比较，输出0或1，用数学式来表达即为左图所示。为表示简洁，通常采用向量的形式来表示，如右图所示，此处我们称W为权重，称b为偏置。

感知机的研究成果让人感到兴奋，我们可以通过对权重和偏置赋予不同值而让感知机实现不同的功能，如与门、与非门、或门。但感知机存在着局限性：一方面是这类算法只能处理线性可分的问题，即它只能表示由一条直线分割的空间。另一方面对于线性不可分的问题，简单的单层感知机没有可行解，一个代表性的例子就是感知机的异或门问题。

02

前馈神经网络

上面我们介绍了感知机，了解到了感知机隐含着表示复杂函数的可能性，也看到了感知的局限性。而解决感知机困境的方法就是将感知机堆叠，进而形成多层神经网络，也称为深度神经网络（Deep Neual Network，DNN）。

神经元

神经元（Neuron）是构成神经网络的基本单元，其主要是模拟生物神经元的结构和特性，接受一组输入信号并产出输出。

现代人工神经元模型由连接、求和节点和激活函数组起，如下图所示，其中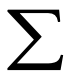表示求和，表示激活函数。

神经元接受n个输入信号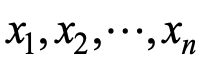，用向量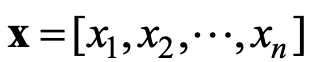表示，神经元中的加权和表示如下：

回顾一下感知机的的表达式

并将其改写成形式

在引入了函数后，感知机就可以写成神经元的形式，输入信号会被转换，转换后的值就是输出。这种将输入信号的总和转换为输出信号的函数称为激活函数（activation function）。 

那么为什么需要使用激活函数呢？又有哪些激活函数可供使用呢？

首先讨论第一个问题，之前介绍的感知机无法解决线性不可分的问题，是因为这类线性模型的表达力不够，从输入到加权求和都是线性运算，而激活函数一般是非线性的，为神经网络引入了非线性因素，这样才能逼近更复杂的数据分布。激活函数也限制了输出的范围，控制该神经元是否激活。

 

激活函数对于神经网络有非常重要的意义，它提升非线性表达能力，缓解梯度消失问题，将特征图映射到新的特征空间以加速网络收敛等。不同的激活函数对神经网络的训练与预测都有不同的影响。常见的激活函数有：ReLU、Sigmoid、Tanh、LReLU、PReLU、ELU等。

网络结构

单一神经元的功能是有限的，需要很多地神经元连接在一起传递信息来协作完成复杂的功能，这就是神经网络。下图给出了一个比较复杂的前馈神经网络。

网络中最左边的一层被称作输入层（input layer），有5个神经元，最右边的一层是输出层（output layer），有2个神经元。网络中处于输入层与输出层之间的层被称作隐层（hidden layer），一个网络中往往有多个隐层。

 

若网络中前一层的所有神经元都与下一层的所有神经元连接，这种结构的网络我们也称为全连接网络（Fully connected network）。

 

神经网络的输入层、输出层设计是比较直观的，其神经元的个数往往是根据数据本身而设定的。例如我们要用神经网络解决手写数字识别的问题，判断一张手写数字图片上面写得是不是“6”。很自然地，我们会将图片像素的灰度值直接作为网络的输入，假设训练样本图片是28×28的灰度图像，那么我们需要28×28=784个输入神经元，每个神经元接受归一化后的灰度值。而输出层只需要一个神经元，输出是否为“6”的置信度，当神经元输出值大于设置的阈值时说明输入图片上写着“6”。

为了更准确地描述神经网络，我们引入一些数学符号：对于一个层的神经网络，第层有个神经元，则层神经元与前一层的连接权重矩阵为

其中表示第l-1层中的第k个神经元与第l层中的第j个神经元的连接。

l-1层到l层的偏置为：

 

l层神经元输入向量为：

l层神经元所用的激活函数为：

l层神经元激活值向量为：

 

前馈神经网络的每一层之间的信息传递方式为为：

也写为

信号流进入前馈神经后，按上式的方式逐层传递，在网络最后输出，整个网络可以看作一个带参数的复合函数：

这就是前馈神经网络的前向传播公式。而对于神经网络中第l层的输出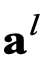，可以看作是原始特征向量X转换到高维空间的特征向量，这个过程称之为特征提取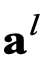，也称为第l层的特征向量或者特征图（feature map）。

训练与预测

与支持向量机、逻辑回归等机器学习算法一样，神经网络也分为训练与预测两个阶段。在训练阶段，需要为神经网络准备好训练数据及对应的标签，通过训练得到一个模型。神经网络的训练就是从数据中学习，其实就是通过不断地修改网络中所有的权重W和偏置b，使得神经网络的输出尽可能地逼近真实的模型的输出。

 

而在预测阶段，在新的测试数据上运行训练好的模型，可以得到分类或者回归的结果。在确定了神经网络的结构后，输入层、隐层、输出层节点数、层与层之间的连接及神经元中使用的激活函数是固定不变的，而对于权重W和偏置b，已由训练得到，可以预测时只需要将新的输入向量从神经网络的输入层送入，沿着网络逐层计算，直到数据流动到输出层并输出结果（一次前向传播），就完成了一次预测并得到了分类或者回归的结果。

 

1.损失函数

 

在神经网络中，衡量网络预测结果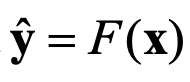与真实值之间差别的指标称为损失函数（loss function），损失函数值越小，表示神经网络的预测结果越接近真实值。

神经网络的训练就是调整权重W和偏置b使得损失函数值尽可能的小，在训练过程中，将损失函数值逐渐收敛，当到达一定轮数或损失函数值小于设定的阈值时训练停止，得到一组使得神经网络拟合真实模型的权重W和偏置b。具体来说，对于一个神经网络F，其权重W和偏置b此时是用随机值来初始化的。给定一个样本(X,Y)，将X输入到神经网络F，经过一次前向传播，得到预测结果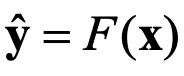，计算损失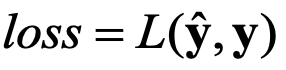，要使得神经网络的预测结果尽可能得接近真实值，就要让损失值尽可能的小，于是神经网络的训练问题演化为一个优化问题，见如下式。

2.参数学习

 

参数学习是神经网络的关键，神经网络使用参数学习算法把从数据中学习到的“知识”保存在参数里面。对于训练集中的每一个样本(X,Y)计算其损失（如均方误差损失），那么在整个训练集上的损失为

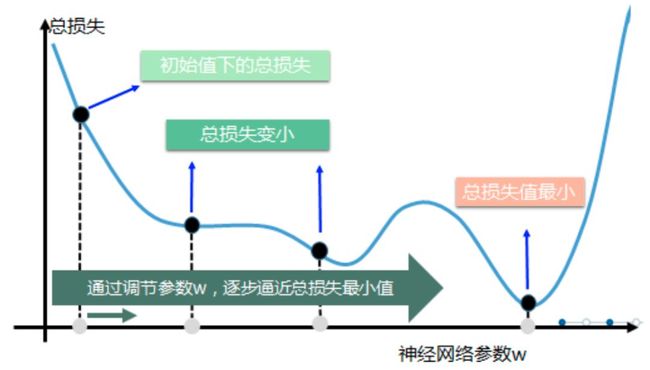
有了目标函数和训练样本，可以通过梯度下降算法来学习神经网络的参数，梯度下降算法原理如下：

上图中曲线表示了在参数W取不同值时，对应损失函数L的大小。梯度下降算法通过调节参数W，使W向着总损失减小的方向移动。参数的梯度可以通过求偏导的方式计算，对于参数其梯度为。有了梯度，还需要定义一个学习率来定义每次参数更新的幅度。从直观上理解，可以认为学习率定义的就是每次参数移动的幅度。对于神经网络中每一个的权重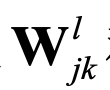和偏置其更新方式为

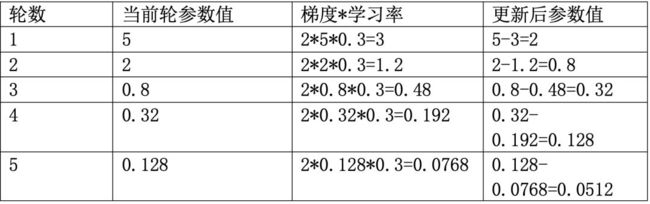
下面通过一个具体的例子来说明梯度下降算法是如何工作的。假设要通过梯度下降算法来优化参数W，使得损失函数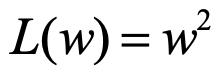的值尽可能小。梯度下降算法的第一步是需要随机产生一个参数W的取值，然后再通过梯度和学习率来更新参数W的取值。在该样例中，参数W的梯度为。假设参数的初始值为5，学习率为0.3，那么这个梯度下降过程可以如下表所示：

经过5次迭代后，参数的值为0.0512，和参数最优值0已经比较接近了。虽然这里给出的是一个比较简单的样例，但是神经网络的参数更新过程是可以类推的。分为两个阶段：第一个阶段先通过前向传播算法得到预测值，并将预测值和真实值做对比得到两者之间的差距。在第二个阶段，通过反向传播算法计算损失函数对每个参数的梯度，然后根据梯度和学习率使用梯度下降算法更新每个参数。此处省略反向传播算法具体的实现方法和数学证明。

 

需要注意的是，梯度下降算法并不能保证被优化的函数达到全局最优解。在训练神经网络时，参数的初始值会很大程度上影响后面的结果。

 

除了不一定能达到全局最优值，梯度下降算法的另一个问题就是计算时间太长。在海量训练数据下，要计算全部训练数据的损失函数是非常耗时的。为了加速训练过程，可以使用随机梯度下降算法（stochastic gradient descent）。这个算法不是在全部训练数据上计算损失函数，而是在每一轮训练中，随机优化某一条训练数据的损失函数，这样参数更新的速度大大加快了。但是问题也很明显，在某一条训练数据上损失函数更小并不代表全部训练数据上损失函数更小，使用随机梯度下降算法优化得到的神经网络可能无法达到局部最优。

 

因此，综合梯度下降算法和随机梯度下降算法的优缺点，在实际应用中一般采用这两个算法的折中：每次计算一小部分训练数据的损失函数，这一小部分数据被称为一个batch。每次在一个batch上优化神经网络的参数并不会比单条数据慢太多，另一方面，每次使用一个batch数据可以大大减小模型收敛所需要的迭代次数。

03

基于飞桨的手写数字识别实战

手写数字识别，顾名思义，就是将带有手写数字的图片输入已经训练过的机器，机器能够很快识别出图片中的手写数字，并打印出结果。手写数字识别问题是深度学习的基础教程，属于典型的图像多分类问题。

 

飞桨简介

 

飞桨以百度多年的深度学习技术研究和业务应用为基础，集深度学习核心框架、基础模型库、端到端开发套件、工具组件和服务平台于一体，2016 年正式开源，是全面开源开放、技术领先、功能完备的产业级深度学习平台。PaddleFluid是飞桨的核心框架，满足模型开发、训练、部署的全流程需求。下面将展示如何用 Paddle FluidAPI 编程并搭建一个简单的神经网络，解决手写数字识别问题。

步骤1：数据准备

MNIST数据集是一个入门级的计算机视觉数据集，包含庞大的手写数字图片，共有60000个训练集和10000测试数据集。分为图片和标签，图片是28*28的像素矩阵，标签为0~9共10个数字。

import numpy as np
import paddle as paddle
import paddle.fluid as fluid
from PIL import Image
import matplotlib.pyplot as plt
import os


BUF_SIZE= 512
BATCH_SIZE = 128
# 用于训练的数据提供器，每次从缓存中随机读取批次大小的数据
train_reader= paddle.batch(
   paddle.reader.shuffle(paddle.dataset.mnist.train(),
                          buf_size=BUF_SIZE),
    batch_size=BATCH_SIZE)
# 用于训练的数据提供器，每次从缓存中随机读取批次大小的数据
test_reader= paddle.batch(
   paddle.reader.shuffle(paddle.dataset.mnist.test(),
                          buf_size=BUF_SIZE),
    batch_size=BATCH_SIZE)

 

飞桨在dataset/mnist.py中实现了MNIST数据集的自动下载和读取，并提供了读取MNIST训练集和测试集的接口paddle.dataset.mnist.train()和paddle.dataset.mnist.test()，且该接口已对图片进行了灰度处理、归一化、居中处理等。

 

构造了训练集提供器train_reader和测试集提供器test_reader，每次会在乱序化后提供大小为BATCH_SIZE的数据，乱序化的大小为缓存大小BUF_SIZE。

步骤2：网络配置

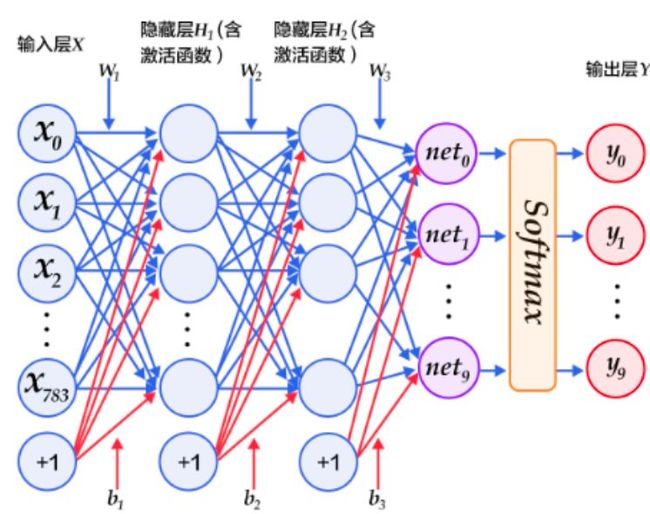
采用了简单的全连接层构造的前馈神经网络，网络结构图如下：

（1）输入层X：MNIST的每张图片为28*28的二维图片，为方便计算，将其向量化为784维向量，即X=(x0,x1, x2,…,x783)。+1代表偏置参数的系数为1。

（2）第一个隐层：全连接层，激活函数为ReLU，节点数设置为100。

（3）第二个隐层：全连接层，激活函数为ReLU，节点数设置为100。

（4）输出层Y：以Softmax为激活函数的全连接输出层。对于有 N 个类别的多分类问题，指定 N 个输出节点，N 维结果向量经过softmax将归一化为 N 个[0,1]范围内的实数值，分别表示该样本属于这 N 个类别的概率。此处的 yi 即对应该图片为数字 i 的预测概率。由于是0~9共10个数字，故将输出层大小设置为10。

def multilayer_perceptron(input):
    # 第一个全连接层，激活函数为ReLU
    hidden1 = fluid.layers.fc(input=input, size=100, act='relu')
    # 第二个全连接层，激活函数为ReLU
    hidden2 = fluid.layers.fc(input=hidden1, size=100, act='relu')
    # 以softmax为激活函数的全连接输出层，大小为10
    prediction = fluid.layers.fc(input=hidden2, size=10, act='softmax')
    return prediction

接下来进行数据层的定义。由于MNIST数据集是单通道的，且图片为28*28像素的，所以输入层image的维度为[None,1,28,28]，label代表图片的类别标签。

# 定义输入输出层
image =fluid.data(name='image', shape=[None,1, 28, 28], dtype='float32')#单通道，28*28像素
label =fluid.layers.data(name='label', shape=[None,1], dtype='int64')  #图片标签

上面我们定义好了前馈神经网络，这里我们使用定义好的网络来获取分类器。

# 获取分类器
predict =multilayer_perceptron(image)

接着是定义损失函数，这里使用的是交叉熵损失函数，该函数在分类任务上比较常用。定义了一个损失函数之后，还要对它求平均值，因为定义的是一个Batch的损失值。同时还可以定义一个准确率函数，可以在训练的时候输出分类的准确率。

# 定义损失函数和准确率函数
cost =fluid.layers.cross_entropy(input=predict, label=label)
avg_cost = fluid.layers.mean(cost)
acc = fluid.layers.accuracy(input=predict, label=label)

接着定义优化算法，这里使用的是Adam优化算法，指定学习率为0.001。

# 定义优化方法
optimizer= fluid.optimizer.AdamOptimizer(learning_rate=0.001)  
opts = optimizer.minimize(avg_cost)

用户完成网络定义后，一段 Fluid 程序中通常存在两个Program：

（1）fluid.default_startup_program：定义了创建模型参数，输入输出，以及模型中可学习参数的初始化等各种操作，由框架自动生成，使用时无需显示地创建；

（2）fluid.default_main_program：定义了神经网络模型，前向反向计算，以及优化算法对网络中可学习参数的更新，使用Fluid的核心就是构建起 default_main_program。

步骤3：模型训练

在上一步骤中定义好了网络模型，即构造好了两个核心Program，接下来将介绍如何使用Excutor来执行Program：

#定义使用CPU还是GPU，使用CPU时use_cuda =False,使用GPU时use_cuda = True
use_cuda =False
place =fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
#创建一个Executor实例exe
exe =fluid.Executor(place)
#正式进行网络训练前，需先执行参数初始化
exe.run(fluid.default_startup_program())

定义好网络训练需要的Executor，在执行训练之前，需要告知网络传入的数据分为两部分，第一部分是image值，第二部分是label值：

feeder= fluid.DataFeeder(place=place, feed_list=[image, label])

之后就可以进行正式的训练了，本实践中设置训练轮数5。在Executor的run方法中，feed代表以字典的形式定义了数据传入网络的顺序，feeder在上述代码中已经进行了定义，将data[0]、data[1]分别传给image、label。fetch_list定义了网络的输出。

在每轮训练中，每100个batch，打印一次训练平均误差和准确率。每轮训练完成后，使用验证集进行一次验证。

EPOCH_NUM= 5
model_save_dir = "./hand.inference.model"
for pass_id in range(EPOCH_NUM):
    # 进行训练
    for batch_id, data in enumerate(train_reader()):  # 遍历train_reader
        train_cost, train_acc = exe.run(program=fluid.default_main_program(),  # 运行主程序
                                        feed=feeder.feed(data),  # 给模型喂入数据
                                        fetch_list=[avg_cost, acc]) # fetch 误差、准确率


        # 每100个batch打印一次信息 误差、准确率
        if batch_id % 100 == 0:
            print('Pass:%d, Batch:%d, Cost:%0.5f,Accuracy:%0.5f' %
                  (pass_id, batch_id, train_cost[0], train_acc[0]))


    # 进行测试
    test_accs = []
    test_costs = []
    # 每训练一轮 进行一次测试
    for batch_id, data in enumerate(test_reader()):                        #遍历test_reader
        test_cost, test_acc = exe.run(program=fluid.default_main_program(),#执行训练程序
                                      feed=feeder.feed(data),           #喂入数据
                                      fetch_list=[avg_cost, acc])      #fetch 误差、准确率
        test_accs.append(test_acc[0])                                  #每个batch的准确率
        test_costs.append(test_cost[0])                                #每个batch的误差
    # 求测试结果的平均值
    test_cost = (sum(test_costs) / len(test_costs))                     #每轮的平均误差
    test_acc = (sum(test_accs) / len(test_accs))                        #每轮的平均准确率
    print('Test:%d, Cost:%0.5f, Accuracy:%0.5f' % (pass_id, test_cost, test_acc))

每轮训练完成后，对模型进行一次保存，使用飞桨提供的fluid.io.save_inference_model()进行模型保存：

# 保存模型
# 如果保存路径不存在就创建
if not os.path.exists(model_save_dir):
    os.makedirs(model_save_dir)
print('save models to %s' % (model_save_dir))
fluid.io.save_inference_model(model_save_dir,  # 保存预测Program的路径
                              ['image'],       #预测需要feed的数据
                              [predict],       #保存预测结果
                              exe)             #executor 保存预测模型

步骤4：模型评估

通过观察训练过程中误差和准确率随着迭代次数的变化趋势，可以对网络训练结果进行评估。

通过上图可以观察到，训练过程中平均误差是在逐步降低的，与此同时，训练的准确率逐步趋近于100%。

步骤5：模型预测

前面已经进行了模型训练，并保存了训练好的模型。接下来就可以使用训练好的模型对手写数字图片进行识别了。

预测之前必须要对预测的图像进行预处理，首先对输入的图片进行灰度化，然后压缩图像大小为28*28，接着将图像转换成一维向量，最后对一维向量进行归一化处理。代码实现如下所示：

def load_image(file):
    im = Image.open(file).convert('L')                        #将RGB转化为灰度图像，像素值在0~255之间
    im = im.resize((28, 28), Image.ANTIALIAS)                 #resize image with high-quality
    im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)#把它变成一个 numpy 数组以匹配数据馈送格式。
    im = im / 255.0 * 2.0 - 1.0                               #归一化到【-1~1】之间
    return im

接下来使用训练好的模型对经过预处理的图片进行预测。首先从指定目录中加载训练好的模型，然后喂入要预测的图片向量，返回模型的输出结果，即为预测概率，这些概率的总和为1。

# 加载数据并开始预测
with fluid.scope_guard(inference_scope):
    #从模型保存路径加载训练好的模型
    [inference_program,                                        #预测用的Program
     feed_target_names,                                        #需要在预测Program 中提供数据的变量的名称。
     fetch_targets] =fluid.io.load_inference_model(model_save_dir,
                                              infer_exe)
    img = load_image(infer_path)
    results = infer_exe.run(program=inference_program,         #运行推测程序
                   feed={feed_target_names[0]: img},           #喂入要预测的img
                   fetch_list=fetch_targets)                   #得到推测结果,

得到各个标签的概率值后，获取概率最大的标签，并打印。

# 获取概率最大的label
lab =np.argsort(results)                             #argsort函数返回的是result数组值从小到大的索引值
print("该图片的预测结果的label为:%d" %lab[0][0][-1]) #-1代表读取数组中倒数第一列

至此，恭喜您！已经成功使用飞桨核心框架 Paddle Fluid 搭建了一个简单的网络。

此实践涉及的全套代码、讲解视频、PPT，已在AI Studio平台上公开，可以点击“阅读原文”加入。

立即体验并运行项目????

立即查看课程视频????

立即获取课程PPT????

 

如果您还想学习更多深度学习课程，这里有从零基础入门到实战进阶的全部内容，而且完全免费，欢迎学习：

https://aistudio.baidu.com/aistudio/course

 

或者您可以参考由中国科学院大学专家、百度深度学习工程师团队共同编著，清华大学出版社出版的《深度学习导论与应用实践》，该教材理论、实践深度结合，源于开源深度学习框架飞桨，独家融合大量实践案例，希望能帮助到想深入了解深度学习或者想进行深度学习实践的您！