欧式空间——正交变换与正交补
文章目录
-
- 正交变换
- 正交补
- 正交投影
- 参考
正交变换
约定 : V : V :V 是 n n n 维欧氏空间.
正交变换: 线性变换 A \mathcal{A} A 满足 ( A α , A β ) = ( α , β ) , ∀ α , β ∈ V . (\mathcal{A} \alpha, \mathcal{A} \beta)=(\alpha, \beta), \forall \alpha, \beta \in V . (Aα,Aβ)=(α,β),∀α,β∈V. 即保持内积的线性变换.
定理1. 设 A \mathcal{A} A 是 V V V 上的线性变换,则如下条件等价:
(1) A \mathcal{A} A 是正交变换,即 ( A α , A β ) = ( α , β ) , ∀ α , β ∈ V (\mathcal{A} \alpha, \mathcal{A} \beta)=(\alpha, \beta), \forall \alpha, \beta \in V (Aα,Aβ)=(α,β),∀α,β∈V;
(2) A \mathcal{A} A 保持长度, 即 ∥ A α ∥ = ∥ α ∥ , ∀ α ∈ V \|\mathcal{A} \alpha\|=\|\alpha\|, \forall \alpha \in V ∥Aα∥=∥α∥,∀α∈V;
(3) A \mathcal{A} A 保持任一标准正交基, 即, 如果 α 1 , ⋯ , α n \alpha_{1}, \cdots, \alpha_{n} α1,⋯,αn 是标准正交基,那么 A α 1 , ⋯ , A α n \mathcal{A} \alpha_{1}, \cdots, \mathcal{A} \alpha_{n} Aα1,⋯,Aαn 也是标准正交基;
(4) A \mathcal{A} A 在任一组标准正交基下的矩阵是正交矩阵.
(5) A \mathcal{A} A 在某组标准正交基下的矩阵是正交矩阵.
(6) A \mathcal{A} A 保持某组标准正交基.
证明: ( 1 ) ⇒ ( 2 ) ∀ α ∈ V , ∥ A α ∥ 2 = ( A α , A α ) = ( α , α ) = ∥ α ∥ 2 ⇒ ∥ A α ∥ = ∥ α ∥ (1) \Rightarrow(2) \forall \alpha \in V, \quad\|\mathcal{A} \alpha\|^{2}=(\mathcal{A} \alpha, \mathcal{A} \alpha)=(\alpha, \alpha)=\|\alpha\|^{2} \Rightarrow\|\mathcal{A} \alpha\|=\|\alpha\| (1)⇒(2)∀α∈V,∥Aα∥2=(Aα,Aα)=(α,α)=∥α∥2⇒∥Aα∥=∥α∥
( 2 ) ⇒ ( 1 ) ∀ α , β ∈ V (2) \Rightarrow(1) \forall \alpha, \beta \in V (2)⇒(1)∀α,β∈V,
∥ A α ∥ = ∥ α ∥ , ∥ A β ∥ = ∥ β ∥ ⇒ ( A α , A α ) = ( α , α ) , ( A β , A β ) = ( β , β ) \|\mathcal{A} \alpha\|=\|\alpha\|,\|\mathcal{A} \beta\|=\|\beta\| \Rightarrow(\mathcal{A} \alpha, \mathcal{A} \alpha)=(\alpha, \alpha),(\mathcal{A} \beta, \mathcal{A} \beta)=(\beta, \beta) ∥Aα∥=∥α∥,∥Aβ∥=∥β∥⇒(Aα,Aα)=(α,α),(Aβ,Aβ)=(β,β)
所以:
( A α + A β , A α + A β ) = ∥ A ( α + β ) ∥ 2 = ∥ α + β ∥ 2 = ( α + β , α + β ) = ∥ α ∥ 2 + ∥ β ∥ 2 + 2 ( α , β ) 又 因 为 ( A α + A β , A α + A β ) = ∥ A α ∥ 2 + ∥ A β ∥ 2 + 2 ( A α , A β ) (\mathcal{A} \alpha+\mathcal{A} \beta, \mathcal{A} \alpha+\mathcal{A} \beta)=\|\mathcal{A}(\alpha+\beta)\|^{2}=\|\alpha+\beta\|^{2}=(\alpha+\beta, \alpha+\beta)\\ =\|\alpha\|^{2}+\|\beta\|^{2}+2(\alpha, \beta)\\ 又因为(\mathcal{A} \alpha+\mathcal{A} \beta, \mathcal{A} \alpha+\mathcal{A} \beta) =\|\mathcal{A} \alpha\|^{2}+\|\mathcal{A} \beta\|^{2}+2(\mathcal{A} \alpha, \mathcal{A} \beta) (Aα+Aβ,Aα+Aβ)=∥A(α+β)∥2=∥α+β∥2=(α+β,α+β)=∥α∥2+∥β∥2+2(α,β)又因为(Aα+Aβ,Aα+Aβ)=∥Aα∥2+∥Aβ∥2+2(Aα,Aβ)
⇒ ( A α , A β ) = ( α , β ) \Rightarrow(\mathcal{A} \alpha, \mathcal{A} \beta)=(\alpha, \beta) ⇒(Aα,Aβ)=(α,β)
( 1 ) ⇒ ( 3 ) : α 1 , ⋯ , α n (1) \Rightarrow(3) :\alpha_{1}, \cdots, \alpha_{n} (1)⇒(3):α1,⋯,αn 是标准正交基 ⇒ ( α i , α j ) = δ i j \Rightarrow\left(\alpha_{i}, \alpha_{j}\right)=\delta_{i j} ⇒(αi,αj)=δij
⇒ ( A α i , A α j ) = ( α i , α j ) = δ i j ⇒ A α 1 , ⋯ , A α n \Rightarrow\left(\mathcal{A} \alpha_{i}, \mathcal{A} \alpha_{j}\right)=\left(\alpha_{i}, \alpha_{j}\right)=\delta_{i j} \Rightarrow \mathcal{A} \alpha_{1}, \cdots, \mathcal{A} \alpha_{n} ⇒(Aαi,Aαj)=(αi,αj)=δij⇒Aα1,⋯,Aαn 是标准正交基.
( 3 ) ⇒ ( 4 ) 任取标准正交基 I : β 1 , ⋯ , β n ( 3 ) ⇒ I I : A β 1 , ⋯ , A β n 是标准正交基 } ⇒ A \left.\begin{array}{l}(3) \Rightarrow(4) \text { 任取标准正交基 } \mathbf{I}: \beta_{1}, \cdots, \beta_{n} \\ (\mathbf{3}) \Rightarrow \mathbf{II}: \mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n} \text { 是标准正交基 }\end{array}\right\} \Rightarrow \mathcal{A} (3)⇒(4) 任取标准正交基 I:β1,⋯,βn(3)⇒II:Aβ1,⋯,Aβn 是标准正交基 }⇒A 在基 I \mathbf{I} I 下的矩阵,
即标准正交基 I I I到标准正交基 I I II II的过渡矩阵, 是正交矩阵.
( 4 ) ⇒ ( 5 ) (4) \Rightarrow(5) (4)⇒(5) 显然.
( 5 ) ⇒ ( 6 ) (\mathbf{5}) \Rightarrow(\mathbf{6}) (5)⇒(6) 设 A \mathcal{A} A在标准正交基 β 1 , ⋯ , β n \beta_{1}, \cdots, \beta_{n} β1,⋯,βn 下的矩阵为正交矩阵 C C C, 即
A ( β 1 , ⋯ , β n ) = ( β 1 , ⋯ , β n ) C , C T C = I n \mathcal{A}\left(\beta_{1}, \cdots, \beta_{n}\right)=\left(\beta_{1}, \cdots, \beta_{n}\right) C, \quad C^{T} C=I_{n} A(β1,⋯,βn)=(β1,⋯,βn)C,CTC=In
下证 A β 1 , ⋯ , A β n \mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n} Aβ1,⋯,Aβn 也是标准正交基:
( A β i , A β j ) = ( ∑ k = 1 n c k i β i , ∑ k = 1 n c k j β j ) = ∑ k = 1 n c k i c k j = ( C T C ) i j = δ i j \left(\mathcal{A} \beta_{i}, \mathcal{A} \beta_{j}\right)=\left(\sum_{k=1}^{n} c_{k i} \beta_{i}, \sum_{k=1}^{n} c_{k j} \beta_{j}\right)=\sum_{k=1}^{n} c_{k i} c_{k j}=\left(C^{T} C\right)_{i j}=\delta_{i j} (Aβi,Aβj)=(k=1∑nckiβi,k=1∑nckjβj)=k=1∑nckickj=(CTC)ij=δij
⇒ A β 1 , ⋯ , A β n \Rightarrow \mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n} ⇒Aβ1,⋯,Aβn 也是标准正交基
( 6 ) ⇒ ( 1 ) (6) \Rightarrow(1) (6)⇒(1)
设 β 1 , ⋯ , β n \beta_{1}, \cdots, \beta_{n} β1,⋯,βn 是标准正交基,且 A β 1 , ⋯ , A β n \mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n} Aβ1,⋯,Aβn 也是标准正交基.
任取 α = ( β 1 , ⋯ , β n ) X , β = ( β 1 , ⋯ , β n ) Y ∈ V \alpha=\left(\beta_{1}, \cdots, \beta_{n}\right) X, \beta=\left(\beta_{1}, \cdots, \beta_{n}\right) Y \in V α=(β1,⋯,βn)X,β=(β1,⋯,βn)Y∈V, 则
A α = A ( β 1 , ⋯ , β n ) X = ( A β 1 , ⋯ , A β n ) X A β = A ( β 1 , ⋯ , β n ) Y = ( A β 1 , ⋯ , A β n ) Y ⇒ ( A α , A β ) = X T Y = ( α , β ) \mathcal{A} \alpha=\mathcal{A}\left(\beta_{1}, \cdots, \beta_{n}\right) X=\left(\mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n}\right) X\\ \mathcal{A} \beta=\mathcal{A}\left(\beta_{1}, \cdots, \beta_{n}\right) Y=\left(\mathcal{A} \beta_{1}, \cdots, \mathcal{A} \beta_{n}\right) Y\\ \Rightarrow(\mathcal{A} \alpha, \mathcal{A} \beta)=\boldsymbol{X}^{T} \boldsymbol{Y}=(\alpha, \beta) Aα=A(β1,⋯,βn)X=(Aβ1,⋯,Aβn)XAβ=A(β1,⋯,βn)Y=(Aβ1,⋯,Aβn)Y⇒(Aα,Aβ)=XTY=(α,β)
( 5 ) ⇒ ( 1 ) (5) \Rightarrow(1) (5)⇒(1) 设 A \mathcal{A} A 在标准正交基 β 1 , ⋯ , β n \beta_{1}, \cdots, \beta_{n} β1,⋯,βn 下的矩阵是正交矩阵 C C C, 即 A ( β 1 , ⋯ , β n ) = ( β 1 , ⋯ , β n ) C , C T C = I n \mathcal{A}\left(\beta_{1}, \cdots, \beta_{n}\right)=\left(\beta_{1}, \cdots, \beta_{n}\right) C, \quad C^{T} C=I_{n} A(β1,⋯,βn)=(β1,⋯,βn)C,CTC=In
任取 α = ( β 1 , ⋯ , β n ) X , β = ( β 1 , ⋯ , β n ) Y \alpha=\left(\beta_{1}, \cdots, \beta_{n}\right) X, \beta=\left(\beta_{1}, \cdots, \beta_{n}\right) Y α=(β1,⋯,βn)X,β=(β1,⋯,βn)Y, 则
( A α , A β ) = ( A [ ( β 1 , ⋯ , β n ) X ] , A [ ( β 1 , ⋯ , β n ) Y ] ) = ( ( A β 1 , ⋯ , A β n ) X , ( A β 1 , ⋯ , A β n ) Y ) = ( ( β 1 , ⋯ , β n ) C X , ( β 1 , ⋯ , β n ) C Y ) = ( C X ) T I n ( C Y ) = X T C T C Y = X T Y = ( α , β ) \begin{aligned}(\mathcal{A} \alpha, \mathcal{A} \beta) &=\left(\mathcal{A}\left[\left(\beta_{1}, \cdots, \beta_{n}\right) X\right], \mathcal{A}\left[\left(\beta_{1}, \cdots, \beta_{n}\right) Y\right]\right) \\ &=\left(\left(\mathcal{A} \boldsymbol{\beta}_{1}, \cdots, \mathcal{A} \boldsymbol{\beta}_{n}\right) \boldsymbol{X},\left(\mathcal{A} \boldsymbol{\beta}_{1}, \cdots, \mathcal{A} \boldsymbol{\beta}_{n}\right) \boldsymbol{Y}\right) \\ &=\left(\left(\beta_{1}, \cdots, \beta_{n}\right) C \boldsymbol{X},\left(\beta_{1}, \cdots, \beta_{n}\right) C \boldsymbol{Y}\right) \\ &=(C \boldsymbol{X})^{T} I_{n}(\boldsymbol{C} \boldsymbol{Y})=\boldsymbol{X}^{T} \boldsymbol{C}^{T} \boldsymbol{C} \boldsymbol{Y}=\boldsymbol{X}^{T} \boldsymbol{Y}=(\alpha, \beta) \end{aligned} (Aα,Aβ)=(A[(β1,⋯,βn)X],A[(β1,⋯,βn)Y])=((Aβ1,⋯,Aβn)X,(Aβ1,⋯,Aβn)Y)=((β1,⋯,βn)CX,(β1,⋯,βn)CY)=(CX)TIn(CY)=XTCTCY=XTY=(α,β)
设 V V V 上正交变换 A \mathcal{A} A 在某标准正交基下的矩阵为 A A A,
定理 1 ⇒ A 1 \Rightarrow A 1⇒A 是正交矩阵 ⇒ det ( A ) = ± 1. \Rightarrow \operatorname{det}(A)=\pm 1 . ⇒det(A)=±1.
注意到 A \mathcal{A} A 在不同基下的矩阵相似,相似矩阵有相同的行列式
A \mathcal{A} A 在任一标准正交基下矩阵的行列式 = det ( A ) . =\operatorname{det}(A) . =det(A).
正交变换在标准正交基下的行列式与基的选取无关!
定义. 设 V V V 上正交变换 A \mathcal{A} A 在某标准正交基下的矩阵为 A A A.
(1) 若 det ( A ) = 1 \operatorname{det}(A)=1 det(A)=1, 则称 A \mathcal{A} A 为第一类正交变换.
(2) 若 det ( A ) = − 1 \operatorname{det}(A)=-1 det(A)=−1, 则称 A \mathcal{A} A 为第二类正交变换.
例 1 \Large{\color{violet}{例1}} 例1. 设 α , β \alpha, \beta α,β 是 n n n 维欧氏空间 V V V 上的两个单位向量.证明: 存在正交变换 A \mathcal{A} A 使得 A α = β . \mathcal{A} \alpha=\beta . Aα=β.
证明: 将 α \alpha α 扩充为 V V V 的一组标准正交基 α = α 1 , α 2 , ⋯ , α n \alpha=\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n} α=α1,α2,⋯,αn, 将 β \beta β 扩充为 V V V 的一组标准正交基 β = β 1 , β 2 , ⋯ , β n \beta=\beta_{1}, \beta_{2}, \cdots, \beta_{n} β=β1,β2,⋯,βn
A α i = β i , 1 ≤ i ≤ n \mathcal{A} \alpha_{i}=\beta_{i}, 1 \leq i \leq \boldsymbol{n} Aαi=βi,1≤i≤n
惟一确定了线性变换 A ∈ End ( V ) : A ( ∑ i = 1 n c i α i ) = ∑ i = 1 n c i β i \mathcal{A} \in \operatorname{End}(V): \mathcal{A}\left(\sum_{i=1}^{n} c_{i} \alpha_{i}\right)=\sum_{i=1}^{n} c_{i} \beta_{i} A∈End(V):A(∑i=1nciαi)=∑i=1nciβi
定理1中 ( 1 ) ⇔ ( 5 ) (1) \Leftrightarrow(5) (1)⇔(5) 表明 A \mathcal{A} A 是正交变换, 此时正交变换 A \mathcal{A} A 满足 A α = β . \mathcal{A} \alpha=\beta . Aα=β.
例 2 \Large{\color{violet}{例2}} 例2设 α , β \alpha, \beta α,β 是 n n n 维欧氏空间 V V V 上的两个单位向量.证明:存在正交变换 A \mathcal{A} A 使得 A α = β \mathcal{A} \alpha=\beta Aα=β 且 dim ker ( A − 1 V ) ≥ n − 2. \operatorname{dim} \operatorname{ker}\left(\mathcal{A}-1_{V}\right) \geq n-2 . dimker(A−1V)≥n−2.
证明: ( 1 ) (1) (1) 若 α , β \alpha, \beta α,β 线性相关, 则 β = ± α . \beta=\pm \alpha . β=±α.
将 α \alpha α 扩充为 V V V 的一组标准正交基 α = α 1 , α 2 , ⋯ , α n \alpha=\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n} α=α1,α2,⋯,αn
⇒ β = ± α 1 , α 2 , ⋯ , α n \Rightarrow \beta=\pm \alpha_{1}, \alpha_{2}, \cdots, \alpha_{n} ⇒β=±α1,α2,⋯,αn 也是一组标准正交基,显然
A α = β , A α i = α i , 2 ≤ i ≤ n \mathcal{A} \alpha=\beta, \mathcal{A} \alpha_{i}=\alpha_{i}, 2 \leq i \leq \boldsymbol{n} Aα=β,Aαi=αi,2≤i≤n
惟一确定了线性变换 A ∈ End ( V ) . \mathcal{A} \in \operatorname{End}(V) . A∈End(V).
定理1中(1) ⇔ ( 5 ) \Leftrightarrow(5) ⇔(5) 表明 A \mathcal{A} A 是正交变换,此时正交变换 A \mathcal{A} A 满足 A α = β \mathcal{A} \alpha=\beta Aα=β 且 dim ( ker A − 1 V ) ≥ n − 1. \operatorname{dim}\left(\operatorname{ker} \mathcal{A}-1_{V}\right) \geq n-1 . dim(kerA−1V)≥n−1.
( 2 ) (2) (2) 下设 α , β \alpha, \beta α,β 线性无关.令单位向量 γ 1 = α + β ∥ α + β ∥ , γ 2 = α − β ∥ α − β ∥ \gamma_{1}=\frac{\alpha+\beta}{\|\alpha+\beta\|}, \gamma_{2}=\frac{\alpha-\beta}{\|\alpha-\beta\|} γ1=∥α+β∥α+β,γ2=∥α−β∥α−β, 则
⇒ ( γ 1 , γ 2 ) = ( α + β ∥ α + β ∥ , α − β ∥ α − β ∥ ) = 1 ∥ α + β ∥ ⋅ ∥ α − β ∥ ( ∥ α ∥ 2 − ∥ β ∥ 2 ) = 0 \Rightarrow\left(\gamma_{1}, \gamma_{2}\right)=\left(\frac{\alpha+\beta}{\|\alpha+\beta\|}, \frac{\alpha-\beta}{\|\alpha-\beta\|}\right)=\frac{1}{\|\alpha+\beta\| \cdot\|\alpha-\beta\|}\left(\|\alpha\|^{2}-\|\beta\|^{2}\right)=\mathbf{0} ⇒(γ1,γ2)=(∥α+β∥α+β,∥α−β∥α−β)=∥α+β∥⋅∥α−β∥1(∥α∥2−∥β∥2)=0
将 γ 1 , γ 2 \gamma_{1}, \gamma_{2} γ1,γ2 扩充为 V V V 的标准正交基 γ 1 , γ 2 , α 3 , ⋯ , α n \gamma_{1}, \gamma_{2}, \alpha_{3}, \cdots, \alpha_{n} γ1,γ2,α3,⋯,αn, 则
A γ 1 = γ 1 , A γ 2 = − γ 2 , A α i = α i ( 3 ≤ i ≤ n ) \mathcal{A} \gamma_{1}=\gamma_{1}, \mathcal{A} \gamma_{2}=-\gamma_{2}, \mathcal{A} \alpha_{i}=\alpha_{i}(3 \leq i \leq n) Aγ1=γ1,Aγ2=−γ2,Aαi=αi(3≤i≤n)
惟一确定了 V V V上的一个正交变换 A . \mathcal{A} . A.
令单位向量 γ 1 = α + β ∥ α + β ∥ , γ 2 = α − β ∥ α − β ∥ ⇒ ( γ 1 , γ 2 ) = 0 \gamma_{1}=\frac{\alpha+\beta}{\|\alpha+\beta\|}, \gamma_{2}=\frac{\alpha-\beta}{\|\alpha-\beta\|} \Rightarrow\left(\gamma_{1}, \gamma_{2}\right)=0 γ1=∥α+β∥α+β,γ2=∥α−β∥α−β⇒(γ1,γ2)=0
将 γ 1 , γ 2 \gamma_{1}, \gamma_{2} γ1,γ2 扩充为 V V V 的标准正交基 γ 1 , γ 2 , α 3 , ⋯ , α n \gamma_{1}, \gamma_{2}, \alpha_{3}, \cdots, \alpha_{n} γ1,γ2,α3,⋯,αn, 正交变换
A γ 1 = γ 1 , A γ 2 = − γ 2 , A α i = α i ( 3 ≤ i ≤ n ) ⇒ α = 1 2 ( ∥ α + β ∥ γ 1 + ∥ α − β ∥ γ 2 ) , β = 1 2 ( ∥ α + β ∥ γ 1 − ∥ α − β ∥ γ 2 ) ⇒ A α = 1 2 ( ∥ α + β ∥ A γ 1 + ∥ α − β ∥ A γ 2 ) = 1 2 ( ∥ α + β ∥ γ 1 − ∥ α − β ∥ γ 2 ) = β \begin{array}{c} \mathcal{A} \gamma_{1}=\gamma_{1}, \mathcal{A} \gamma_{2}=-\gamma_{2}, \mathcal{A} \alpha_{i}=\alpha_{i}(3 \leq i \leq n) \\ \Rightarrow \alpha=\frac{1}{2}\left(\|\alpha+\beta\| \gamma_{1}+\|\alpha-\beta\| \gamma_{2}\right), \quad \beta=\frac{1}{2}\left(\|\alpha+\beta\| \gamma_{1}-\|\alpha-\beta\| \gamma_{2}\right) \\ \Rightarrow \mathcal{A} \alpha=\frac{1}{2}\left(\|\alpha+\beta\| \mathcal{A} \gamma_{1}+\|\alpha-\beta\| \mathcal{A} \gamma_{2}\right) \\ =\frac{1}{2}\left(\|\alpha+\beta\| \gamma_{1}-\|\alpha-\beta\| \gamma_{2}\right)=\beta \end{array} Aγ1=γ1,Aγ2=−γ2,Aαi=αi(3≤i≤n)⇒α=21(∥α+β∥γ1+∥α−β∥γ2),β=21(∥α+β∥γ1−∥α−β∥γ2)⇒Aα=21(∥α+β∥Aγ1+∥α−β∥Aγ2)=21(∥α+β∥γ1−∥α−β∥γ2)=β
显然 span ( α 3 , ⋯ , α n ) ⊆ ker ( A − 1 V ) ⇒ dim ker ( A − 1 V ) ≥ n − 2 \operatorname{span}\left(\alpha_{3}, \cdots, \alpha_{n}\right) \subseteq \operatorname{ker}\left(\mathcal{A}-1_{V}\right) \Rightarrow \operatorname{dim} \operatorname{ker}\left(\mathcal{A}-1_{V}\right) \geq n-2 span(α3,⋯,αn)⊆ker(A−1V)⇒dimker(A−1V)≥n−2
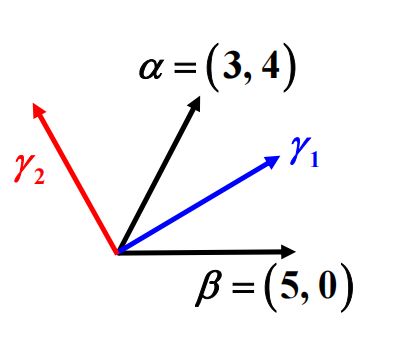
例 3 \Large{\color{violet}{例3}} 例3 . 设 α = ( 3 , 4 ) , β = ( 5 , 0 ) \alpha=(3,4), \beta=(5,0) α=(3,4),β=(5,0), 试求正交矩阵 A A A 使得 A α = β . A \alpha=\beta . Aα=β.
解: 显然 ∥ α ∥ = ∥ β ∥ = 5 \|\alpha\|=\|\beta\|=5 ∥α∥=∥β∥=5 且 α , β \alpha, \beta α,β 线性无关.
令 γ 1 = α + β ∥ α + β ∥ = 1 5 ( 2 , 1 ) T , γ 2 = α − β ∥ α − β ∥ = 1 5 ( − 1 , 2 ) \gamma_{1}=\frac{\alpha+\beta}{\|\alpha+\beta\|}=\frac{1}{\sqrt{5}}(2,1)^{T}, \gamma_{2}=\frac{\alpha-\beta}{\|\alpha-\beta\|}=\frac{1}{\sqrt{5}}(-1,2) γ1=∥α+β∥α+β=51(2,1)T,γ2=∥α−β∥α−β=51(−1,2),
⇒ ( γ 1 , γ 2 ) = 0 ⇒ γ 1 ⊥ γ 2 \Rightarrow\left(\gamma_{1}, \gamma_{2}\right)=0 \Rightarrow \gamma_{1} \perp \gamma_{2} ⇒(γ1,γ2)=0⇒γ1⊥γ2, 令 A ∈ R 2 × 2 A \in \mathbb{R}^{2 \times 2} A∈R2×2 满足:
A γ 1 = γ 1 , A γ 2 = − γ 2 A \gamma_{1}=\gamma_{1}, A \gamma_{2}=-\gamma_{2} Aγ1=γ1,Aγ2=−γ2
即 A ( γ 1 , γ 2 ) = ( γ 1 , γ 2 ) ( 1 0 0 − 1 ) A\left(\gamma_{1}, \gamma_{2}\right)=\left(\gamma_{1}, \gamma_{2}\right)\left(\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right) A(γ1,γ2)=(γ1,γ2)(100−1)
⇒ A = C ( 1 0 0 − 1 ) C T = 1 5 ( 2 − 1 1 2 ) ( 1 0 0 − 1 ) ( 2 1 − 1 2 ) = 1 5 ( 3 4 4 − 3 ) ⇒ A 正交且 A α = β \Rightarrow A=C\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) C^{T}=\frac{1}{5}\left(\begin{array}{cc} 2 & -1 \\ 1 & 2 \end{array}\right)\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\left(\begin{array}{cc} 2 & 1 \\ -1 & 2 \end{array}\right)=\frac{1}{5}\left(\begin{array}{cc} 3 & 4 \\ 4 & -3 \end{array}\right) \Rightarrow A \text { 正交且 } A \alpha=\beta ⇒A=C(100−1)CT=51(21−12)(100−1)(2−112)=51(344−3)⇒A 正交且 Aα=β
正交补
设 V 1 , V 2 V_{1}, V_{2} V1,V2 是 V V V 的子空间, β ∈ V . \beta \in V . β∈V.
β \beta β 与 V 1 V_{1} V1 正交 ( β ⊥ V 1 ) : \left(\beta \perp V_{1}\right): (β⊥V1): 若 ( α , β ) = 0 , ∀ α ∈ V 1 (\alpha, \beta)=0, \forall \alpha \in V_{1} (α,β)=0,∀α∈V1.
V 1 V_{1} V1 与 V 2 V_{2} V2 正交 ( V 1 ⊥ V 2 ) : \left(V_{1} \perp V_{2}\right): (V1⊥V2): 若 ( α , γ ) = 0 , ∀ α ∈ V 1 , γ ∈ V 2 . (\alpha, \gamma)=0, \forall \alpha \in V_{1}, \gamma \in V_{2} . \quad (α,γ)=0,∀α∈V1,γ∈V2. 即 α ⊥ V 2 , ∀ α ∈ V 1 . \alpha \perp V_{2}, \forall \alpha \in V_{1} . α⊥V2,∀α∈V1.
例 1 \Large{\color{violet}{例1}} 例1. V = R 4 , V 1 = { ( a , 0 , 0 , d ) ∣ a , d ∈ R , a + d = 0 } V=\mathbb{R}^{4}, V_{1}=\{(a, 0,0, d) \mid a, d \in \mathbb{R}, a+d=0\} V=R4,V1={ (a,0,0,d)∣a,d∈R,a+d=0}
β = ( 1 , 0 , 0 , 1 ) , V 2 = { ( 0 , b , c , 0 ) ∣ b , c ∈ R } ⇒ β ⊥ V 1 , β ⊥ V 2 , V 1 ⊥ V 2 \beta=(1,0,0,1), V_{2}=\{(0, b, c, 0) \mid b, c \in \mathbb{R}\} \Rightarrow \beta \perp V_{1}, \beta \perp V_{2}, V_{1} \perp V_{2} β=(1,0,0,1),V2={ (0,b,c,0)∣b,c∈R}⇒β⊥V1,β⊥V2,V1⊥V2
定理2. 设 W , V 1 , V 2 , ⋯ , V s W, V_{1}, V_{2}, \cdots, V_{s} W,V1,V2,⋯,Vs 都是 V V V 的子空间, 则
( 1 ) V 1 ⊥ V 2 ⇒ V 1 + V 2 (1) V_{1} \perp V_{2} \Rightarrow V_{1}+V_{2} (1)V1⊥V2⇒V1+V2 是直和.
(2) W ⊥ V i ⇒ W ⊥ ∑ i = 1 s V i W \perp V_{i} \Rightarrow W \perp \sum_{i=1}^{s} V_{i} W⊥Vi⇒W⊥∑i=1sVi.
( 3 ) V 1 , V 2 , ⋯ , V s (3) V_{1}, V_{2}, \cdots, V_{s} (3)V1,V2,⋯,Vs 两两正交 ⇒ V 1 + V 2 + ⋯ + V s \Rightarrow V_{1}+V_{2}+\cdots+V_{s} ⇒V1+V2+⋯+Vs 是直和.
证明: ( 1 ) (1) (1) 只需证明 V 1 ∩ V 2 = O . V_{1} \cap V_{2}=O . V1∩V2=O.任取 α ∈ V 1 ∩ V 2 \alpha \in V_{1} \cap V_{2} α∈V1∩V2,
α ∈ V 1 α ∈ V 2 V 1 ⊥ V 2 } ⇒ ( α , α ) = 0 ⇒ α = 0 ⇒ V 1 ∩ V 2 = O ⇒ V 1 + V 2 \left.\begin{array}{l}\alpha \in V_{1} \\ \alpha \in V_{2} \\ V_{1} \perp V_{2}\end{array}\right\} \Rightarrow(\alpha, \alpha)=0 \quad \Rightarrow \alpha=0 \quad \Rightarrow V_{1} \cap V_{2}=O \Rightarrow V_{1}+V_{2} α∈V1α∈V2V1⊥V2⎭⎬⎫⇒(α,α)=0⇒α=0⇒V1∩V2=O⇒V1+V2 是直和
( 2 ) (2) (2) 任取 w ∈ W , α = ∑ i = 1 s α i ∈ ∑ i = 1 s V i w \in W, \alpha=\sum_{i=1}^{s} \alpha_{i} \in \sum_{i=1}^{s} V_{i} w∈W,α=∑i=1sαi∈∑i=1sVi, 其中 α i ∈ V i \alpha_{i} \in V_{i} αi∈Vi :
W ⊥ V i ⇒ ( w , α i ) = 0 ⇒ ( w , α ) = ( w , ∑ i = 1 s α i ) = ∑ i = 1 s ( w , α i ) = 0 ⇒ W ⊥ ∑ i = 1 s V i . \begin{aligned} W \perp V_{i} & \Rightarrow\left(w, \alpha_{i}\right)=0 \\ & \Rightarrow(w, \alpha)=\left(w, \sum_{i=1}^{s} \alpha_{i}\right)=\sum_{i=1}^{s}\left(w, \alpha_{i}\right)=0 \Rightarrow W \perp \sum_{i=1}^{s} V_{i} . \end{aligned} W⊥Vi⇒(w,αi)=0⇒(w,α)=(w,i=1∑sαi)=i=1∑s(w,αi)=0⇒W⊥i=1∑sVi.
( 3 ) (3) (3) 任取 i : ( 2 ) ⇒ V i ⊥ ( ∑ j ≠ i V j ) ⇒ ( 1 ) V i ∩ ( ∑ j ≠ i V j ) = O ⇒ V 1 + V 2 + ⋯ + V s i: \quad(2) \Rightarrow \quad V_{i} \perp\left(\sum_{j \neq i} V_{j}\right) \underset{(1)}{\Rightarrow} V_{i} \cap\left(\sum_{j \neq i} V_{j}\right)=O \Rightarrow V_{1}+V_{2}+\cdots+V_{s} i:(2)⇒Vi⊥(∑j=iVj)(1)⇒Vi∩(∑j=iVj)=O⇒V1+V2+⋯+Vs 是直和
设 V 1 V_{1} V1 是 V V V 的 r r r 维子空间, 令
V 1 ⊥ : = { α ∈ V ∣ α ⊥ V 1 } = { α ∈ V ∣ ( α , α 1 ) = 0 , ∀ α 1 ∈ V 1 } V_{1}^{\perp}:=\left\{\alpha \in V \mid \alpha \perp V_{1}\right\}=\left\{\alpha \in V \mid\left(\alpha, \alpha_{1}\right)=0, \forall \alpha_{1} \in V_{1}\right\} V1⊥:={ α∈V∣α⊥V1}={ α∈V∣(α,α1)=0,∀α1∈V1}
则 V 1 ⊥ V_{1}^{\perp} V1⊥ 是 V V V 的子空间.
V 1 ⊥ V 1 ⊥ ⇒ V 1 + V 1 ⊥ 是直和 ⇒ dim ( V 1 ⊥ ) = dim ( V 1 + V 1 ⊥ ) − dim V 1 ≤ n − r V_{1} \perp V_{1}^{\perp} \Rightarrow V_{1}+V_{1}^{\perp} \text { 是直和 } \Rightarrow \operatorname{dim}\left(V_{1}^{\perp}\right)=\operatorname{dim}\left(V_{1}+V_{1}^{\perp}\right)-\operatorname{dim} V_{1} \leq n-r V1⊥V1⊥⇒V1+V1⊥ 是直和 ⇒dim(V1⊥)=dim(V1+V1⊥)−dimV1≤n−r
取 V 1 V_{1} V1 的正交基 α 1 , ⋯ , α r \alpha_{1}, \cdots, \alpha_{r} α1,⋯,αr, 扩充为 V V V 的正交基 α 1 , ⋯ , α r , β 1 , ⋯ , β n − r \alpha_{1}, \cdots, \alpha_{r}, \beta_{1}, \cdots, \beta_{n-r} α1,⋯,αr,β1,⋯,βn−r
则 ( α i , β j ) = 0 , ∀ i , j ⇒ β j ∈ V 1 ⊥ ⇒ span ( β 1 , ⋯ , β n − r ) ⊆ V 1 ⊥ ⇒ dim V 1 ⊥ ≥ dim span ( β 1 , ⋯ , β n − r ) = n − r ⇒ V 1 ⊥ 是 V 的 一 个 与 V 1 正 交 的 补 子 空 间 . \begin{aligned} \text { 则 }\left(\alpha_{i}, \beta_{j}\right)=0, \forall i, j & \Rightarrow \beta_{j} \in V_{1}^{\perp} \Rightarrow \operatorname{span}\left(\beta_{1}, \cdots, \beta_{n-r}\right) \subseteq V_{1}^{\perp} \\ & \Rightarrow \operatorname{dim} V_{1}^{\perp} \geq \operatorname{dim} \operatorname{span}\left(\beta_{1}, \cdots, \beta_{n-r}\right)=n-r \\ &\Rightarrow V_{1}^{\perp} 是 V 的一个与 V_{1} 正交的补子空间. \end{aligned} 则 (αi,βj)=0,∀i,j⇒βj∈V1⊥⇒span(β1,⋯,βn−r)⊆V1⊥⇒dimV1⊥≥dimspan(β1,⋯,βn−r)=n−r⇒V1⊥是V的一个与V1正交的补子空间.
进而, 显然有 : V 2 ⊥ V 1 ⇒ V 2 ⊆ V 1 ⊥ V 1 ⊥ : V 1 : V_{2} \perp V_{1} \Rightarrow V_{2} \subseteq V_{1}^{\perp} \quad V_{1}^{\perp}: V_{1} :V2⊥V1⇒V2⊆V1⊥V1⊥:V1 的正交补
定理3. 设 V 1 V_{1} V1 是 V V V 的 r r r 维子空间, 那么 V V V 有一个惟一的子空间 V 1 ⊥ = { α ∈ V ∣ α ⊥ V 1 } V_{1}^{\perp}=\left\{\alpha \in V \mid \alpha \perp V_{1}\right\} V1⊥={ α∈V∣α⊥V1}.使得 V 1 ⊥ V 1 ⊥ V_{1} \perp V_{1}^{\perp} V1⊥V1⊥ 且有直和 V 1 ⊕ V 1 ⊥ = V . V_{1} \oplus V_{1}^{\perp}=V . V1⊕V1⊥=V. 进而 V 2 ⊥ V 1 ⇒ V 2 ⊆ V 1 ⊥ . V_{2} \perp V_{1} \Rightarrow V_{2} \subseteq V_{1}^{\perp} . V2⊥V1⇒V2⊆V1⊥.
例 2 \Large{\color{violet}{例2}} 例2. 设 α = ( 1 , 1 , 1 ) \alpha=(1,1,1) α=(1,1,1), 求 V 1 = span ( α ) V_{1}=\operatorname{span}(\alpha) V1=span(α) 在 R 3 \mathbb{R}^{3} R3 中的正交补 V 1 ⊥ V_{1}^{\perp} V1⊥ 的一组标准正交基.
解1: V 1 ⊥ = { α ∈ V ∣ α ⊥ V 1 } = { ( x 1 , x 2 , x 3 ) ∣ x 1 + x 2 + x 3 = 0 } \quad V_{1}^{\perp}=\left\{\alpha \in V \mid \alpha \perp V_{1}\right\}=\left\{\left(x_{1}, x_{2}, x_{3}\right) \mid x_{1}+x_{2}+x_{3}=0\right\} V1⊥={ α∈V∣α⊥V1}={ (x1,x2,x3)∣x1+x2+x3=0}
方程组 x 1 + x 2 + x 3 = 0 x_{1}+x_{2}+x_{3}=0 x1+x2+x3=0 的基础解系为 ( − 1 , 1 , 0 ) T , ( − 1 , 0 , 1 ) T (-1,1,0)^{T},(-1,0,1)^{T} (−1,1,0)T,(−1,0,1)T
⇒ V 1 ⊥ 有一组基 : ( − 1 , 1 , 0 ) , ( − 1 , 0 , 1 ) \Rightarrow V_{1}^{\perp} \text { 有一组基 }:(-1,1,0),(-1,0,1) ⇒V1⊥ 有一组基 :(−1,1,0),(−1,0,1)
正交化 : δ 1 = ( − 1 , 1 , 0 ) , δ 2 = 1 2 ( − 1 , − 1 , 2 ) : \delta_{1}=(-1,1,0), \delta_{2}=\frac{1}{2}(-1,-1,2) :δ1=(−1,1,0),δ2=21(−1,−1,2)
单位化得 V 1 V_{1} V1 得 V 1 ⊥ V_{1}^{\perp} V1⊥ 的一组标准正交基 : 1 2 ( − 1 , 1 , 0 ) , 1 6 ( − 1 , − 1 , 2 ) : \frac{1}{\sqrt{2}}(-1,1,0), \frac{1}{\sqrt{6}}(-1,-1,2) :21(−1,1,0),61(−1,−1,2)
解2: 将 α \alpha α 扩充为 R 3 \mathbb{R}^{3} R3 的一组基: α = ( 1 , 1 , 1 ) , α 2 = ( 1 , 1 , 0 ) , α 3 = ( 1 , 0 , 0 ) \alpha=(1,1,1), \alpha_{2}=(1,1,0), \alpha_{3}=(1,0,0) α=(1,1,1),α2=(1,1,0),α3=(1,0,0)
正交化:
β 1 = α = ( 1 , 1 , 1 ) β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 = ⋯ = 1 3 ( 1 , 1 , − 2 ) β 3 = ⋯ = 1 2 ( 1 , − 1 , 0 ) \begin{array}{l} \beta_{1}=\alpha=(1,1,1)\\ \beta_{2}=\alpha_{2}-\frac{\left(\alpha_{2}, \beta_{1}\right)}{\left(\beta_{1}, \beta_{1}\right)} \beta_{1}=\cdots=\frac{1}{3}(1,1,-2) \\ \beta_{3}=\cdots=\frac{1}{2}(1,-1,0) \end{array} β1=α=(1,1,1)β2=α2−(β1,β1)(α2,β1)β1=⋯=31(1,1,−2)β3=⋯=21(1,−1,0)
将 β 2 , β 3 \beta_{2}, \beta_{3} β2,β3 单位化,得 V 1 ⊥ V_{1}^{\perp} V1⊥ 的一组标准正交基: γ 2 = 1 6 ( 1 , 1 , − 2 ) , γ 3 = 1 2 ( 1 , − 1 , 0 ) \gamma_{2}=\frac{1}{\sqrt{6}}(1,1,-2), \gamma_{3}=\frac{1}{\sqrt{2}}(1,-1,0) γ2=61(1,1,−2),γ3=21(1,−1,0)
例 2 \Large{\color{violet}{例2}} 例2 设 V = R 2 × 2 , ( A , B ) = Tr ( A T B ) , V 1 = { A ∈ R 2 × 2 ∣ A T = A } V=\mathbb{R}^{2 \times 2},(A, B)=\operatorname{Tr}\left(A^{T} B\right), V_{1}=\left\{A \in \mathbb{R}^{2 \times 2} \mid A^{T}=A\right\} V=R2×2,(A,B)=Tr(ATB),V1={ A∈R2×2∣AT=A}, 求 V 1 ⊥ . V_{1}^{\perp} . V1⊥.
解: 选取 V 1 V_{1} V1 的一组基 : A 1 = ( 1 0 0 0 ) , A 2 = ( 0 1 1 0 ) , A 3 = ( 0 0 0 1 ) : A_{1}=\left(\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right), A_{2}=\left(\begin{array}{ll}0 & 1 \\ 1 & 0\end{array}\right), A_{3}=\left(\begin{array}{ll}0 & 0 \\ 0 & 1\end{array}\right) :A1=(1000),A2=(0110),A3=(0001)
显然 dim V 1 = 3 , dim V 1 ⊥ = 1. \operatorname{dim} V_{1}=3, \operatorname{dim} V_{1}^{\perp}=1 . dimV1=3,dimV1⊥=1.
B = ( a b c d ) ∈ V 1 ⊥ ⇔ ( B , A i ) = 0 , i = 1 , 2 , 3 B=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right) \in V_{1}^{\perp} \Leftrightarrow\left(B, A_{i}\right)=0, i=1,2,3 B=(acbd)∈V1⊥⇔(B,Ai)=0,i=1,2,3
0 = ( A 1 , B ) = Tr ( 1 0 0 0 ) ( a b c d ) = Tr ( a b 0 0 ) = a ⇒ a = 0 0=\left(A_{1}, B\right)=\operatorname{Tr}\left(\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right)\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)=\operatorname{Tr}\left(\begin{array}{ll}a & b \\ 0 & 0\end{array}\right)=a \Rightarrow a=0 0=(A1,B)=Tr(1000)(acbd)=Tr(a0b0)=a⇒a=0
0 = ( A 2 , B ) = ⋯ = b + c ⇒ b + c = 0 0=\left(A_{2}, B\right)=\cdots=b+c \Rightarrow b+c=0 0=(A2,B)=⋯=b+c⇒b+c=0
0 = ( A 3 , B ) = ⋯ = d ⇒ d = 0 ⇔ B = b ( 0 1 − 1 0 ) ⇒ V 1 ⊥ = { A ∈ R 2 × 2 ∣ A T = − A } 0=\left(A_{3}, B\right)=\cdots=d \Rightarrow d=0 \Leftrightarrow B=b\left(\begin{array}{cc}0 & 1 \\ -1 & 0\end{array}\right) \Rightarrow V_{1}^{\perp}=\left\{A \in \mathbb{R}^{2 \times 2} \mid A^{T}=-A\right\} 0=(A3,B)=⋯=d⇒d=0⇔B=b(0−110)⇒V1⊥={ A∈R2×2∣AT=−A}
例 3 \Large{\color{violet}{例3}} 例3. 设 V = R n × n , ( A , B ) = Tr ( A T B ) , V 1 = { A ∈ R n × n ∣ A T = A } , 求 V 1 ⊥ . V=\mathbb{R}^{n \times n},(A, B)=\operatorname{Tr}\left(A^{T} B\right), V_{1}=\left\{A \in \mathbb{R}^{n \times n} \mid A^{T}=A\right\}, 求 V_{1}^{\perp} . V=Rn×n,(A,B)=Tr(ATB),V1={ A∈Rn×n∣AT=A},求V1⊥.
解: V 1 V_{1} V1 有一组基: E i j + E j i ( 1 ≤ i ≤ j ≤ n ) , dim V 1 = n ( n + 1 ) 2 E_{i j}+E_{j i}(1 \leq i \leq j \leq n), \operatorname{dim} V_{1}=\frac{n(n+1)}{2} Eij+Eji(1≤i≤j≤n),dimV1=2n(n+1)
令 V 2 = { A ∈ R n × n ∣ A T = − A } V_{2}=\left\{A \in \mathbb{R}^{n \times n} \mid A^{T}=-A\right\} V2={ A∈Rn×n∣AT=−A} 表示反对称矩阵子空间. dim V 2 = n ( n − 1 ) 2 = dim V 1 ⊥ \quad \operatorname{dim} V_{2}=\frac{n(n-1)}{2}=\operatorname{dim} V_{1}^{\perp} dimV2=2n(n−1)=dimV1⊥.
断言: V 1 ⊥ V 2 V_{1} \perp V_{2} V1⊥V2, 于是 V 2 ⊆ V 1 ⊥ ∀ A ∈ V 1 , B ∈ V 2 V_{2} \subseteq V_{1}^{\perp} \quad \forall A \in V_{1}, B \in V_{2} V2⊆V1⊥∀A∈V1,B∈V2,
( A , B ) = Tr ( A T B ) = Tr ( A T B ) T = Tr ( B T A ) = Tr ( − B A ) = − Tr ( B A ) = − Tr ( A B ) = − Tr ( A T B ) = − ( A , B ) ⇒ ( A , B ) = 0 ⇒ A ⊥ B ⇒ V 2 ⊆ V 1 ⊥ ⇒ V 1 ⊥ = { A ∈ R 2 × 2 ∣ A T = − A } \begin{aligned}(A, B) &=\operatorname{Tr}\left(A^{T} B\right)=\operatorname{Tr}\left(A^{T} B\right)^{T}=\operatorname{Tr}\left(B^{T} A\right) \\ &=\operatorname{Tr}(-B A)=-\operatorname{Tr}(B A)=-\operatorname{Tr}(A B)=-\operatorname{Tr}\left(A^{T} B\right) \\ &=-(A, B) \Rightarrow(A, B)=0 \Rightarrow A \perp B \Rightarrow V_{2} \subseteq V_{1}^{\perp} \Rightarrow V_{1}^{\perp}=\left\{A \in \mathbb{R}^{2 \times 2} \mid A^{T}=-A\right\} \end{aligned} (A,B)=Tr(ATB)=Tr(ATB)T=Tr(BTA)=Tr(−BA)=−Tr(BA)=−Tr(AB)=−Tr(ATB)=−(A,B)⇒(A,B)=0⇒A⊥B⇒V2⊆V1⊥⇒V1⊥={ A∈R2×2∣AT=−A}
正交投影
V 1 V_{1} V1 是 V V V 的子空间 ⇒ V = V 1 ⊕ V 1 ⊥ ⇒ \Rightarrow V=V_{1} \oplus V_{1}^{\perp} \Rightarrow ⇒V=V1⊕V1⊥⇒ 任一 α ∈ V \alpha \in V α∈V 可以惟一地分解为: α = α 1 + α 1 ⊥ \alpha=\alpha_{1}+\alpha_{1}^{\perp} α=α1+α1⊥,其中 α 1 ∈ V 1 , α 1 ⊥ ∈ V 1 ⊥ , α 1 \alpha_{1} \in V_{1}, \alpha_{1}^{\perp} \in V_{1}^{\perp}, \quad \alpha_{1} α1∈V1,α1⊥∈V1⊥,α1 称为 α \alpha α 在 V 1 V_{1} V1 上的正交投影,或内射影.
例 1 \Large{\color{violet}{例1}} 例1. ( 1 ) V = R 3 , V 1 = span ( ε 1 , ε 3 ) ⇒ V 1 ⊥ = span ( ε 2 ) (1) V=\mathbb{R}^{3}, V_{1}=\operatorname{span}\left(\varepsilon_{1}, \varepsilon_{3}\right) \Rightarrow V_{1}^{\perp}=\operatorname{span}\left(\varepsilon_{2}\right) (1)V=R3,V1=span(ε1,ε3)⇒V1⊥=span(ε2)
α = ( a , b , c ) ⇒ α \alpha=(a, b, c) \Rightarrow \alpha α=(a,b,c)⇒α 在 V 1 V_{1} V1 上的正交投影为 ( a , 0 , c ) . (a, 0, c) . (a,0,c).
( 2 ) V = R n × n , ( A , B ) = Tr ( A T B ) , V 1 = { A ∈ R n × n ∣ A T = A } (2) V=\mathbb{R}^{n \times n},(A, B)=\operatorname{Tr}\left(A^{T} B\right), V_{1}=\left\{A \in \mathbb{R}^{n \times n} \mid A^{T}=A\right\} (2)V=Rn×n,(A,B)=Tr(ATB),V1={ A∈Rn×n∣AT=A}
A ∈ R n × n ⇒ A = 1 2 ( A + A T ) + 1 2 ( A − A T ) ⇒ A 在 V 1 A \in \mathbb{R}^{n \times n} \Rightarrow A=\frac{1}{2}\left(A+A^{T}\right)+\frac{1}{2}\left(A-A^{T}\right) \Rightarrow A 在 V_{1} A∈Rn×n⇒A=21(A+AT)+21(A−AT)⇒A在V1 上的正交投影为 1 2 ( A T + A ) \frac{1}{2}\left(A^{T}+A\right) 21(AT+A)
定理4. 设 V 1 V_{1} V1 是 V V V 的子空间, α ∈ V , α 1 ∈ V 1 \alpha \in V, \alpha_{1} \in V_{1} α∈V,α1∈V1,则如下条件等价:
(1) α 1 \alpha_{1} α1 是 α \alpha α 在 V 1 V_{1} V1 上的正交投影;
(3) α − α 1 ⊥ V 1 \alpha-\alpha_{1} \perp V_{1} α−α1⊥V1
(2) ∥ α − α 1 ∥ ≤ ∥ α − β ∥ , ∀ β ∈ V 1 ; \left\|\alpha-\alpha_{1}\right\| \leq\|\alpha-\beta\|, \forall \beta \in V_{1} ; ∥α−α1∥≤∥α−β∥,∀β∈V1;
证明: ( 1 ) ⇒ ( 2 ) \quad(1) \Rightarrow(2) (1)⇒(2)
α 1 是 α 在 V 1 上的正交投影 ⇒ α − α 1 ∈ V 1 ⊥ ∀ β ∈ V 1 , α − β = ( α − α 1 ) + ( α 1 − β ) α 1 − β ∈ V 1 } ⇒ ∥ α − α 1 ∥ ≤ ∥ α − β ∥ \left.\begin{array}{r}\alpha_{1} \text { 是 } \alpha \text { 在 } V_{1} \text { 上的正交投影 } \Rightarrow \alpha-\alpha_{1} \in V_{1}^{\perp} \\ \forall \beta \in V_{1}, \alpha-\beta=\left(\alpha-\alpha_{1}\right)+\left(\alpha_{1}-\beta\right) \\ \alpha_{1}-\beta \in V_{1}\end{array}\right\} \Rightarrow\left\|\alpha-\alpha_{1}\right\| \leq\|\alpha-\beta\| α1 是 α 在 V1 上的正交投影 ⇒α−α1∈V1⊥∀β∈V1,α−β=(α−α1)+(α1−β)α1−β∈V1⎭⎬⎫⇒∥α−α1∥≤∥α−β∥
( 1 ) ⇒ ( 3 ) (1) \Rightarrow(3) (1)⇒(3) 由正交投影定义.
( 3 ) ⇒ ( 1 ) α − α 1 ⊥ V 1 ⇒ α − α 1 ∈ V 1 ⊥ α = α 1 + ( α − α 1 ) , α 1 ∈ V 1 } ⇒ α 1 \left.\begin{array}{r}(3) \Rightarrow(1) \alpha-\alpha_{1} \perp V_{1} \Rightarrow \alpha-\alpha_{1} \in V_{1}^{\perp} \\ \alpha=\alpha_{1}+\left(\alpha-\alpha_{1}\right), \alpha_{1} \in V_{1}\end{array}\right\} \Rightarrow \alpha_{1} (3)⇒(1)α−α1⊥V1⇒α−α1∈V1⊥α=α1+(α−α1),α1∈V1}⇒α1 是 α \alpha α 在 V 1 V_{1} V1 上正交投影
( 2 ) ⇒ ( 1 ) \quad(2) \Rightarrow(1) (2)⇒(1)
设 α 在 V 1 上的正交投影为 γ ⇒ α − γ ∈ V 1 ⊥ α 1 , γ ∈ V 1 ⇒ γ − α 1 ∈ V 1 } ⇒ \left.\begin{array}{r}\alpha \text { 在 } V_{1} \text { 上的正交投影为 } \gamma \Rightarrow \alpha-\gamma \in V_{1}^{\perp} \\ \alpha_{1}, \gamma \in V_{1} \Rightarrow \gamma-\alpha_{1} \in V_{1}\end{array}\right\} \Rightarrow α 在 V1 上的正交投影为 γ⇒α−γ∈V1⊥α1,γ∈V1⇒γ−α1∈V1}⇒
勾股定理 ⇒ ∥ α − α 1 ∥ 2 = ∥ α − γ ∥ 2 + ∥ γ − α 1 ∥ 2 \Rightarrow\left\|\alpha-\alpha_{1}\right\|^{2}=\|\alpha-\gamma\|^{2}+\left\|\gamma-\alpha_{1}\right\|^{2} ⇒∥α−α1∥2=∥α−γ∥2+∥γ−α1∥2
⇒ ∥ α − α 1 ∥ ≥ ∥ α − γ ∥ ( 2 ) ⇒ ∥ α − α 1 ∥ ≤ ∥ α − γ ∥ } ⇒ ∥ α − α 1 ∥ = ∥ α − γ ∥ \left.\qquad \begin{array}{rl}\Rightarrow & \left\|\alpha-\alpha_{1}\right\| \geq\|\alpha-\gamma\| \\ (2) & \Rightarrow\left\|\alpha-\alpha_{1}\right\| \leq\|\alpha-\gamma\|\end{array}\right\} \Rightarrow\left\|\alpha-\alpha_{1}\right\|=\|\alpha-\gamma\| ⇒(2)∥α−α1∥≥∥α−γ∥⇒∥α−α1∥≤∥α−γ∥}⇒∥α−α1∥=∥α−γ∥
⇒ ∥ γ − α 1 ∥ = 0 ⇒ γ = α 1 \Rightarrow\left\|\gamma-\alpha_{1}\right\|=0 \Rightarrow \gamma=\alpha_{1} ⇒∥γ−α1∥=0⇒γ=α1
例 2 \Large{\color{violet}{例2}} 例2. 设 α = ( 1 , 2 , 3 ) , β 1 = ( 1 , 1 , 0 ) , β 2 = ( 1 , 0 , 1 ) ∈ R 3 \alpha=(1,2,3), \beta_{1}=(1,1,0), \beta_{2}=(1,0,1) \in \mathbb{R}^{3} α=(1,2,3),β1=(1,1,0),β2=(1,0,1)∈R3, 求 α \alpha α 在
V 1 = span ( β 1 , β 2 ) 上的正交投影 V_{1}=\operatorname{span}\left(\beta_{1}, \beta_{2}\right) \text { 上的正交投影 } V1=span(β1,β2) 上的正交投影
解: α 1 = c 1 β 1 + c 2 β 2 \alpha_{1}=c_{1} \beta_{1}+c_{2} \beta_{2} α1=c1β1+c2β2 是 α \alpha α 在 V 1 V_{1} V1 上的正交投影
⇔ α − α 1 ⊥ V 1 = span ( β 1 , β 2 ) ⇔ { ( α − c 1 β 1 − c 2 β 2 , β 1 ) = 0 ( α − c 1 β 1 − c 2 β 2 , β 2 ) = 0 ⇔ { c 1 ( β 1 , β 1 ) + c 2 ( β 2 , β 1 ) = ( α , β 1 ) , c 1 ( β 1 , β 2 ) + c 2 ( β 2 , β 2 ) = ( α , β 2 ) ( ( β 1 , β 1 ) ( β 1 , β 2 ) ( β 1 , β 2 ) ( β 2 , β 2 ) ∣ ( α , β 1 ) ( α , β 2 ) ) = ( 2 1 3 1 2 4 ) → ⋯ → ( 1 0 2 / 3 0 1 5 / 3 ) ⇒ α 1 = 2 3 β 1 + 5 3 β 2 = 1 3 ( 7 , 2 , 5 ) \begin{array}{l} \Leftrightarrow \alpha-\alpha_{1} \perp V_{1}=\operatorname{span}\left(\beta_{1}, \beta_{2}\right) \Leftrightarrow\left\{\begin{array}{l} \left(\alpha-c_{1} \beta_{1}-c_{2} \beta_{2}, \beta_{1}\right)=0 \\ \left(\alpha-c_{1} \beta_{1}-c_{2} \beta_{2}, \beta_{2}\right)=0 \end{array}\right. \\ \Leftrightarrow\left\{\begin{array}{l} c_{1}\left(\beta_{1}, \beta_{1}\right)+c_{2}\left(\beta_{2}, \beta_{1}\right)=\left(\alpha, \beta_{1}\right), \\ c_{1}\left(\beta_{1}, \beta_{2}\right)+c_{2}\left(\beta_{2}, \beta_{2}\right)=\left(\alpha, \beta_{2}\right) \end{array}\right. \\ \quad\left(\begin{array}{ll} \left(\beta_{1}, \beta_{1}\right) & \left(\beta_{1}, \beta_{2}\right) \\ \left(\beta_{1}, \beta_{2}\right) & \left(\beta_{2}, \beta_{2}\right) \end{array} \mid \begin{array}{l} \left(\alpha, \beta_{1}\right) \\ \left(\alpha, \beta_{2}\right) \end{array}\right)=\left(\begin{array}{ll|l} 2 & 1 & 3 \\ 1 & 2 & 4 \end{array}\right) \rightarrow \cdots \rightarrow\left(\begin{array}{ll|l} 1 & 0 & 2 / 3 \\ 0 & 1 & 5 / 3 \end{array}\right) \\ \Rightarrow \alpha_{1}=\frac{2}{3} \beta_{1}+\frac{5}{3} \beta_{2}=\frac{1}{3}(7,2,5) \end{array} ⇔α−α1⊥V1=span(β1,β2)⇔{ (α−c1β1−c2β2,β1)=0(α−c1β1−c2β2,β2)=0⇔{ c1(β1,β1)+c2(β2,β1)=(α,β1),c1(β1,β2)+c2(β2,β2)=(α,β2)((β1,β1)(β1,β2)(β1,β2)(β2,β2)∣(α,β1)(α,β2))=(211234)→⋯→(10012/35/3)⇒α1=32β1+35β2=31(7,2,5)
例 3 \Large{\color{violet}{例3}} 例3:设 α , β 1 , ⋯ , β s ∈ R n \alpha, \beta_{1}, \cdots, \beta_{s} \in \mathbb{R}^{n} α,β1,⋯,βs∈Rn, 求 α \alpha α 在 V 1 = span ( β 1 , ⋯ , β s ) V_{1}=\operatorname{span}\left(\beta_{1}, \cdots, \beta_{s}\right) V1=span(β1,⋯,βs) 上的正交投影.
解: α 1 = c 1 β 1 + ⋯ + c s β s \alpha_{1}=c_{1} \beta_{1}+\cdots+c_{s} \beta_{s} α1=c1β1+⋯+csβs 是 α \alpha α 在 V 1 V_{1} V1 上的正交投影
⇔ α − α 1 ⊥ V 1 = span ( β 1 , ⋯ , β s ) ⇔ ( α − ∑ i = 1 s c i β i , β j ) = 0 ⇔ ∑ i = 1 s c i ( β i , β j ) = ( α , β j ) \begin{array}{l} \Leftrightarrow \alpha-\alpha_{1} \perp V_{1}=\operatorname{span}\left(\beta_{1}, \cdots, \beta_{s}\right) \\ \Leftrightarrow\left(\alpha-\sum_{i=1}^{s} c_{i} \beta_{i}, \beta_{j}\right)=0 \\ \Leftrightarrow \sum_{i=1}^{s} c_{i}\left(\beta_{i}, \beta_{j}\right)=\left(\alpha, \beta_{j}\right) \end{array} ⇔α−α1⊥V1=span(β1,⋯,βs)⇔(α−∑i=1sciβi,βj)=0⇔∑i=1sci(βi,βj)=(α,βj)
⇔ ( c 1 , ⋯ , c s ) T \Leftrightarrow\left(c_{1}, \cdots, c_{s}\right)^{T} ⇔(c1,⋯,cs)T 是 B T B X = B T α B^{T} B X=B^{T} \alpha BTBX=BTα 的解, 其中
其中 B = ( β 1 , ⋯ , β s ) , B T B B=\left(\beta_{1}, \cdots, \beta_{s}\right), B^{T} B B=(β1,⋯,βs),BTB 是 β 1 , ⋯ , β s \beta_{1}, \cdots, \beta_{s} β1,⋯,βs 的Gram 矩阵
参考
高等代数 电子科技大学