李宏毅2021春季机器学习课程视频笔记1:Introduction, Colab & PyTorch Tutorials, HW1
诸神缄默不语-个人CSDN博文目录
李宏毅2021春季机器学习课程视频笔记集合
文章目录
- 1. Introduction
- 2. Colab Tutorial
- 3. PyTorch Tutorial
-
- 3.1 PyTorch Tutorial 1
- 3.2 PyTorch Tutorial 2
- 4. HW1
-
- 4.1 任务介绍
- 4.2 simple baseline
- 4.3 medium baseline
- 4.4 strong baseline(我没有突破到……)
-
- 4.4.1 Hints
- 4.4.2 我的调参心得
- 4.4.3 详细介绍调参工作
1. Introduction
- 建议先修
- 数学:微积分、线性代数、概率论
- 编程:课程任务都提供Python示例代码,要求能阅读并基于示例代码进行修改和优化。课程中不会教NumPy,Matplotlib等。
- 硬件:如果能上Google的话,课程作业都通过Google Colab完成,无本机硬件配置要求。
- 机器学习的本质就是寻找一个函数function,来寻找一个输入input与输出output之间的映射关系。可以是输入一段语音,输出这段语音对应的文字;也可以输入一张图,输出这张图的内容;也可以输入一场棋局,输出下一步应该走哪一格。

- 根据函数输出结果,可以将机器学习分为三类:
①回归任务regression,输出是一个标量。
②分类任务classification,输出是一个类别。
③结构化学习structured learning,产生结构化的输出,如图像、文档等。 - 下面以预测YouTube频道次日流量为例,讲一个回归任务的流程。
数据是每日流量组成的时间序列。
以下主要有两部分重点,一是讲述模型学习的三步骤(建立模型、定义算法、优化参数),二是从线性模型到神经网络-
首先以当日流量作为自变量 x x x,预测次日流量 y y y。
整个深度学习模型的步骤如下图所示:建立模型、定义算法、优化参数

- 第一步:建立一个含有未知参数的函数,这个函数就是机器学习里的模型model。
具体选择建立什么样的函数需要一定的domain knowledge。
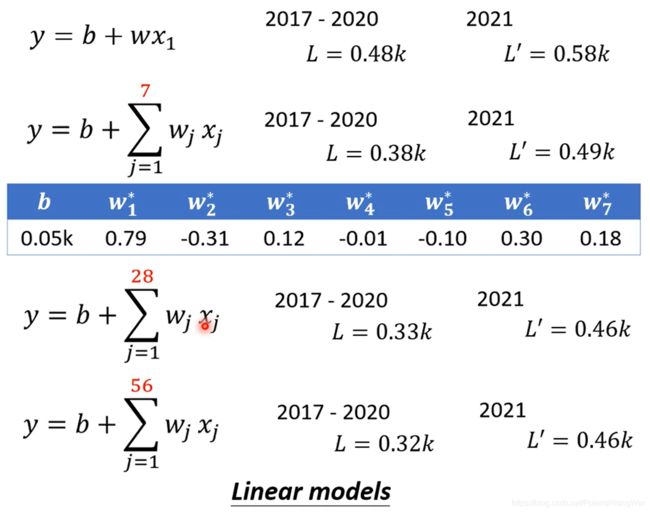
在这里我们先建立模型: y = b + w x 1 y=b+wx_1 y=b+wx1。其中 x x x是已知的特征feature; w w w是权重weight, b b b是偏置bias,都是未知的参数,需要从数据中学习。 - 第二步:用训练数据定义损失Loss
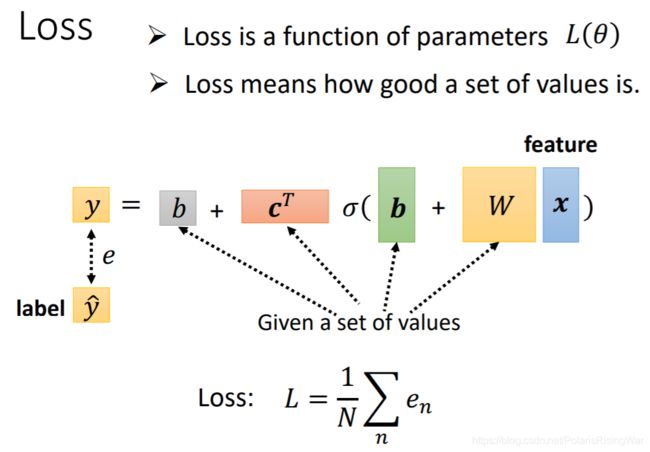
损失函数 L ( b , w ) L(b,w) L(b,w), L L L越小说明参数越好。
损失函数的计算过程:对每一个训练样本,计算其模型输出与真实值(label)之间的误差(e),整个模型的损失函数就是全部训练样本误差的平均值。
不同的误差计算方式:MAE / MSE / Cross-entropy
Error Surface误差曲面:绘制出参数和L之间的映射关系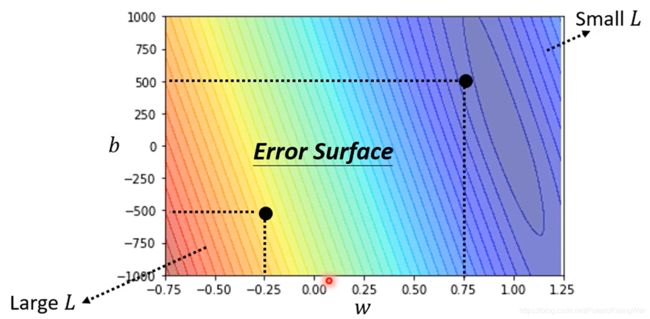
- 第三步:优化Optimization
优化的目标是找到使L最小的参数,即求解 w ∗ , b ∗ = a r g min w , b L w^*,b^*=arg\min\limits_{w,b}L w∗,b∗=argw,bminL
优化方法:梯度下降gradient descend- 以一个参数 w w w举例,画出其对应的error surface
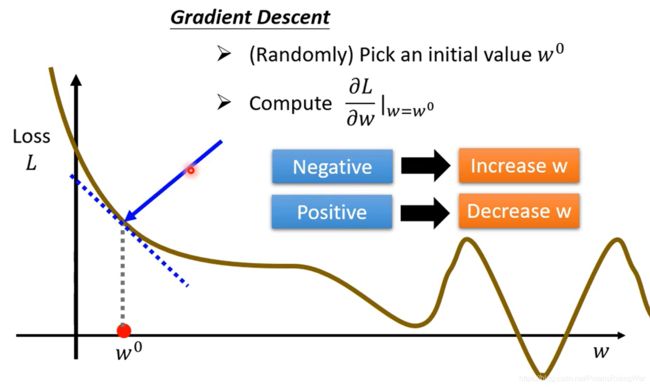
先随便选个 w w w,然后计算它的梯度
梯度,也就是斜率,当梯度为负时就应增大 w w w
注意图片中的error surface是个假的,但是在真实情况下loss确实可能非负。如果以MAE或MSE来计算不会为负,但loss本身可以随便设
增大x的幅度(步长)由学习率learning rate和斜率决定。学习率是一个需要提前设定的超参数hyperparameter(相比超参而言, w w w 和 b b b 这种参数是要通过数据学习的)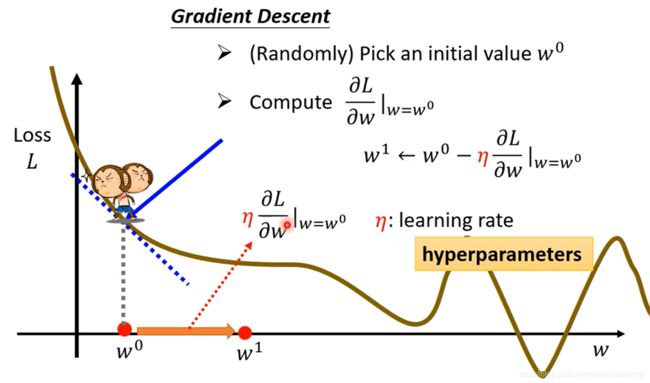
如此迭代多次更新 w w w(停止条件:迭代次数达到阈值(超参)或微分趋于0)
梯度下降的问题在于只能找到局部最小值(但其实这是个假问题,将在后面课程中解释) - 推广到两个参数的例子:随机选取初始参数,计算其偏微分,使用梯度下降的方式同时更新两个参数,多次迭代直至停止。

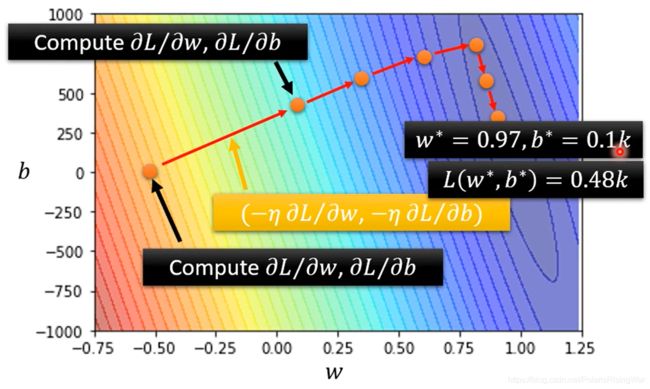
- PyTorch等深度学习框架都能自动计算微分1
- 以一个参数 w w w举例,画出其对应的error surface
- 第四步:测试
通过训练阶段得到 w ∗ = 0.97 , b ∗ = 0.1 k w^*=0.97,b^*=0.1k w∗=0.97,b∗=0.1k,训练集上的损失函数 L ( w ∗ , b ∗ ) = 0.48 k L(w^*,b^*)=0.48k L(w∗,b∗)=0.48k,测试集上的损失函数 L ′ = 0.58 k L'=0.58k L′=0.58k
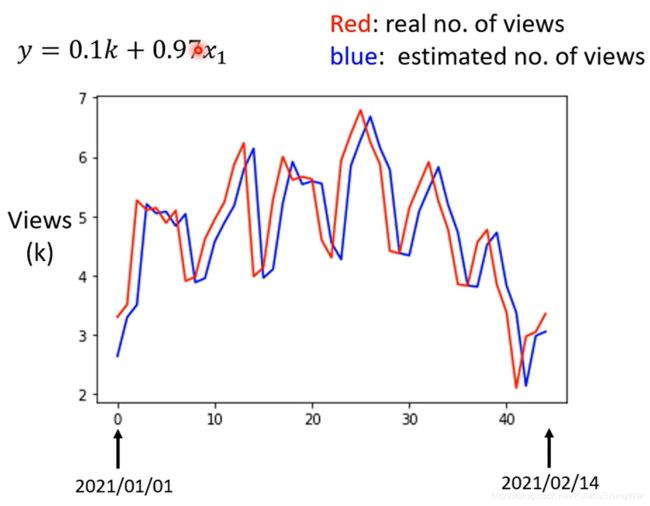
通过上图真实值和拟合值对比,可以看出数据有明显的周期性,因此修改自变量为前j日的流量。
- 第一步:建立一个含有未知参数的函数,这个函数就是机器学习里的模型model。
-
从线性模型到神经网络
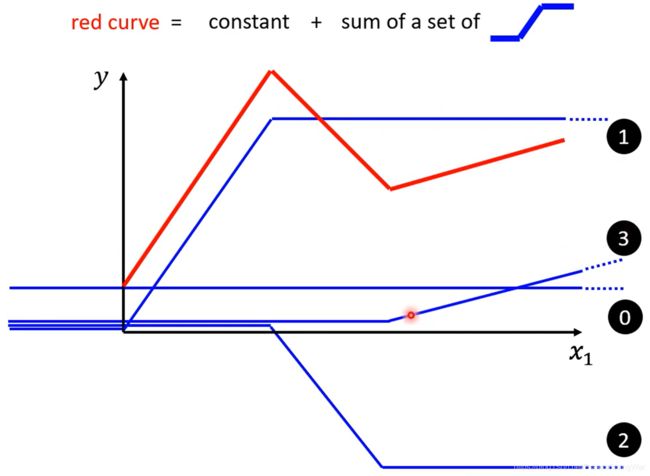
上面的那种模型都是线性模型linear model,但是线性模型太简单,不管怎么调参数都只是一条直线(下图蓝线),无法拟合复杂的真实情况(如下图红线),因此我们需要换一种更有弹性的模型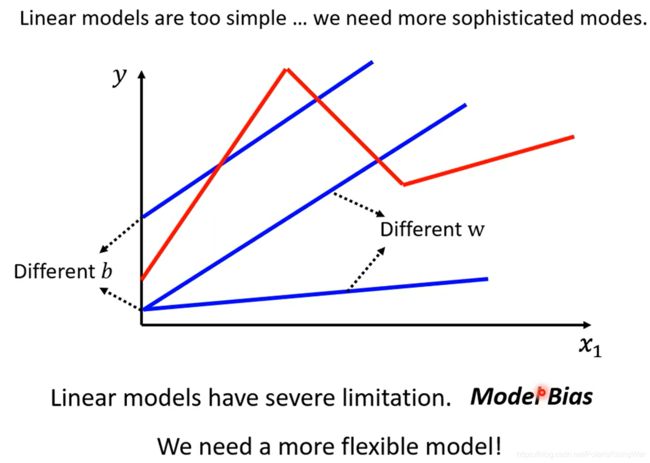
这种模型本身的限制叫做model bias(注意跟模型参数bias不一样)
在YouTube上这一部分的视频评论中,李老师回复称这里的model bias就是inductive bias -
事实上任何分段线性函数piecewise linear curve(就是像红线这种每一段都是直线的曲线)都可以用一系列这种蓝线来加总拟合,不是piecewise linear curve的曲线也可以近似成piecewise linear curve
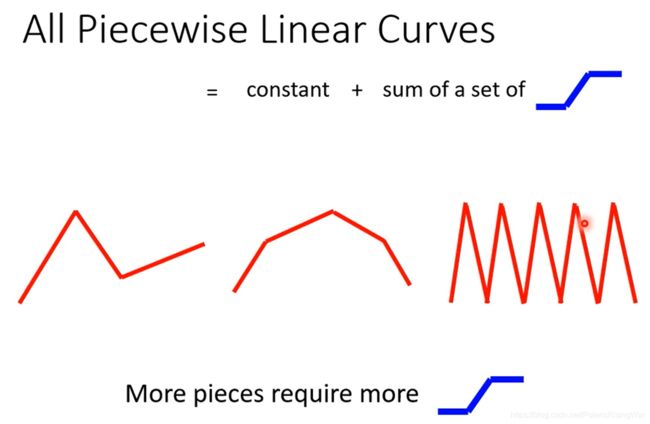
-
这种蓝线(hard sigmoid)可以用sigmoid来拟合
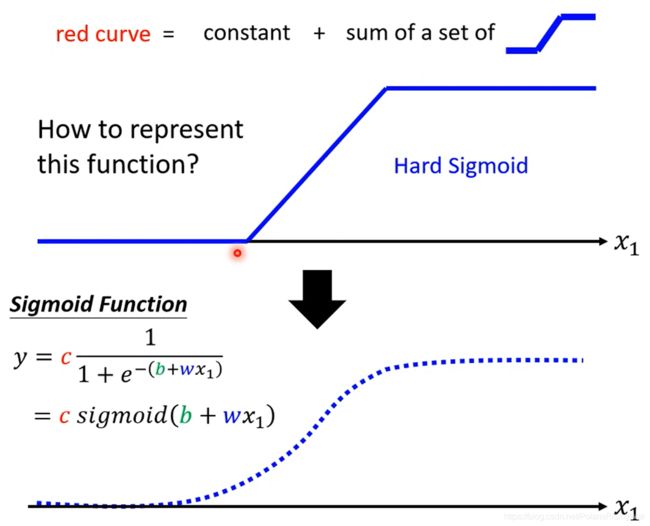
不同的参数( c c c b b b w w w) → 不同的sigmoid function → 组合逼近出不同的piece linear function → 近似得到不同的continuous function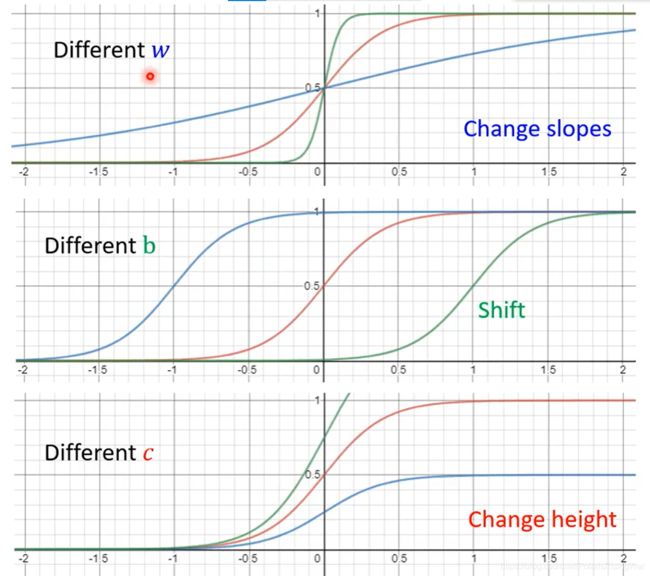
来自弹幕:
为什么需要非线性变化?用于拟合hard sigmoid
为什么需要不同参数?为了得到不同的hard sigmoid -
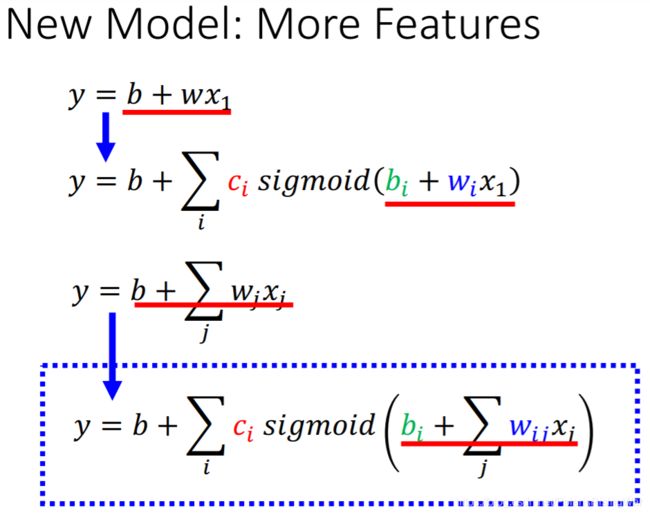
最后合出来的红线(真实情况)就可以写成这样的公式: y = b + ∑ i c i y=b+\sum\limits_{i}c_i y=b+i∑ci s i g m o i d ( b i + w i x 1 ) sigmoid(b_i+w_ix_1) sigmoid(bi+wix1),如图所示
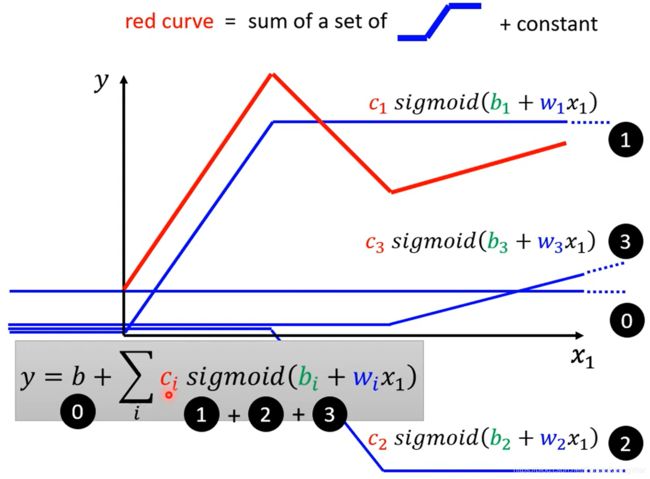
-
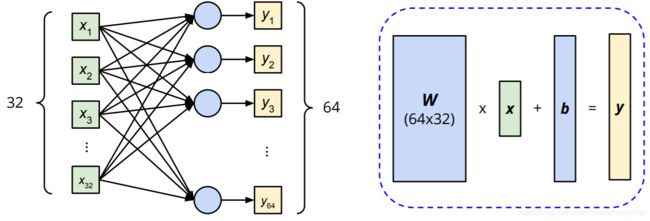
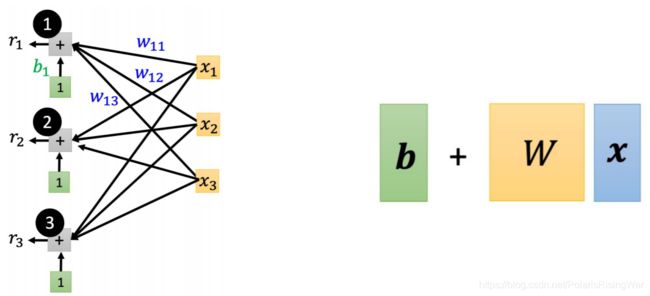
用直观的方式画出这个新模型
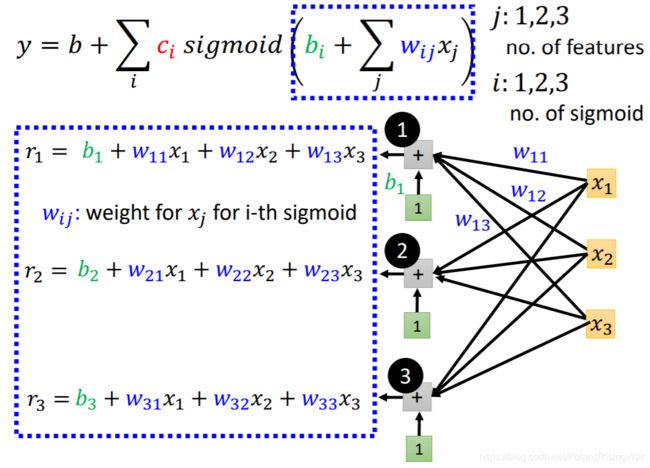
将三个式子简化为矩阵形式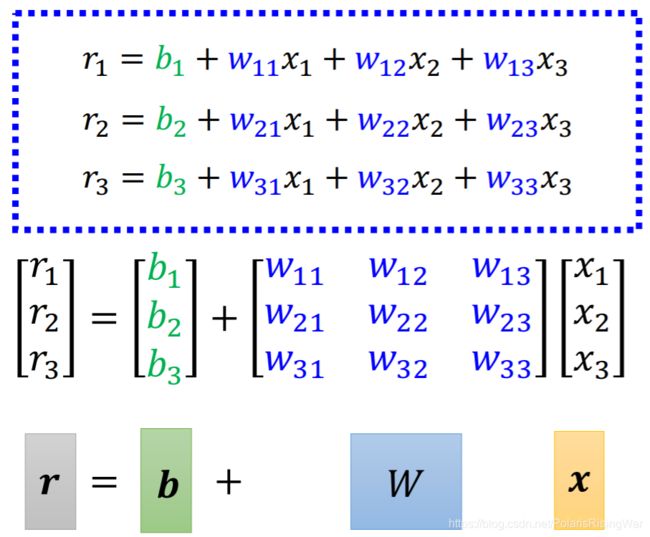
σ \sigma σ表示做sigmoid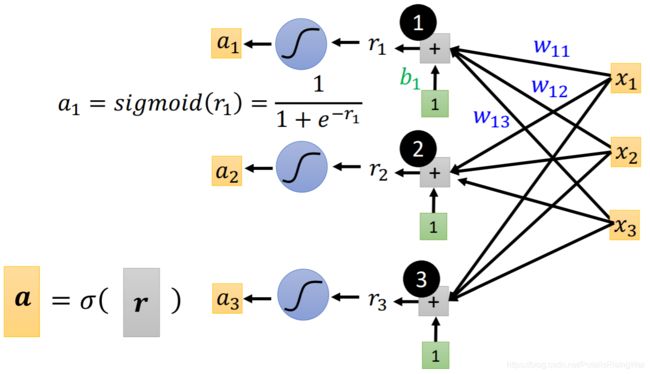
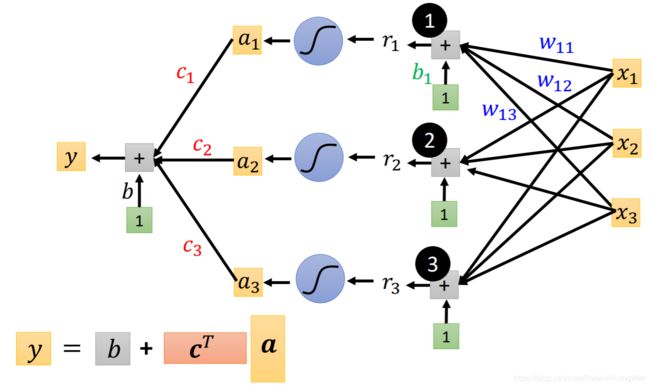
将这三个式子连起来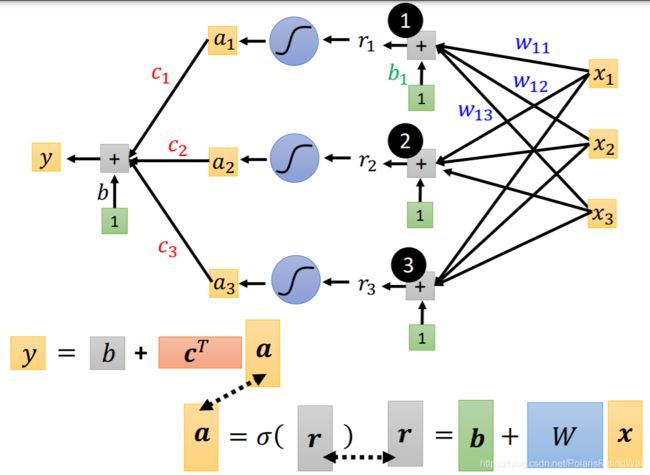
就得到了模型最后的式子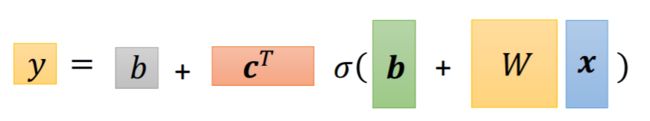
-
将未知参数排成一个向量( W W W 拿行和拿列是一样的)组成 θ \theta θ(就是下文优化部分用的)
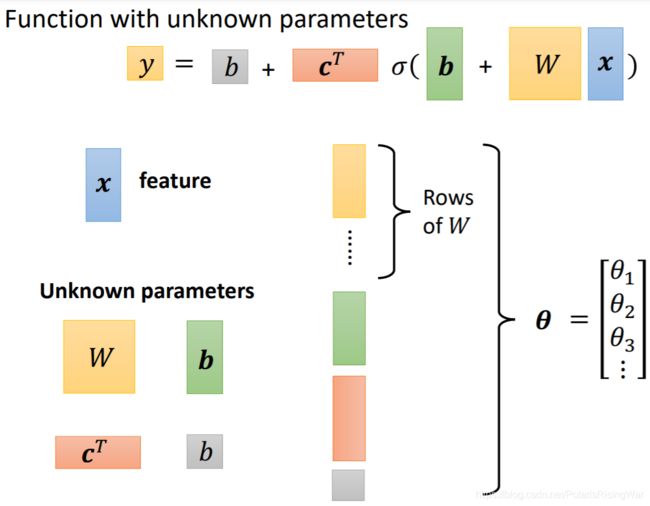
老师答疑环节:
①注意这个sigmoid的数目是可以自己定的(就是神经网络里的神经元的数目是可以自己定的),而且sigmoid越多,可以产生出的piecewise linear function就越复杂(可以产生和sigmoid一样多的线段)
②不用hard sigmoid是因为公式难写出来,其实也可以用 -
在实际运行中,不会一次运行所有数据,而会用batch:将整个数据分成很多batch,每次运行一个batch,update一次参数;将所有batch运行完一次,是为一个epoch。
batch size是需要设置的超参。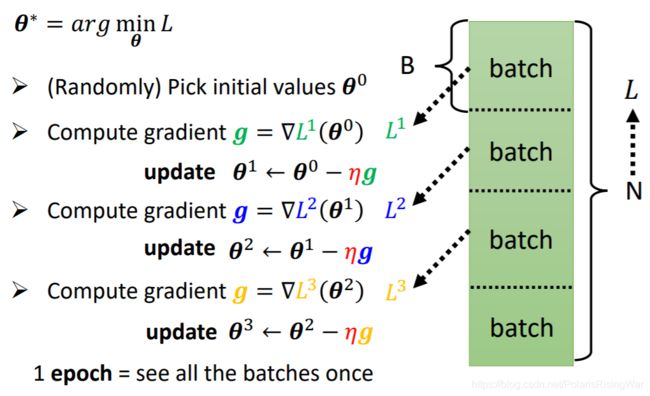
-
从Sigmoid到ReLU
hard sigmoid可以看作是两个ReLU加起来,如图所示: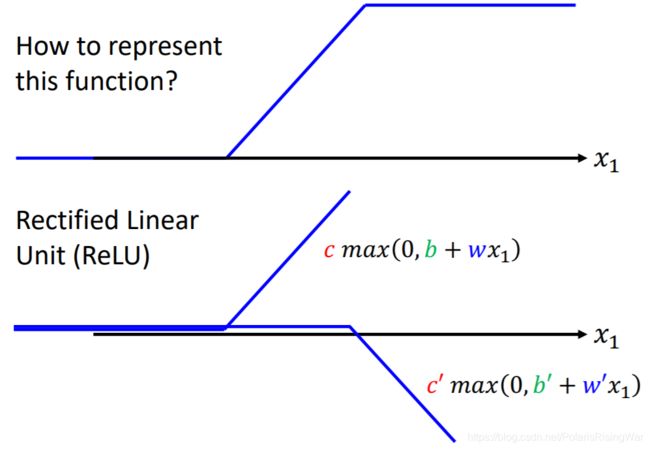
所以Sigmoid也可以换成ReLU: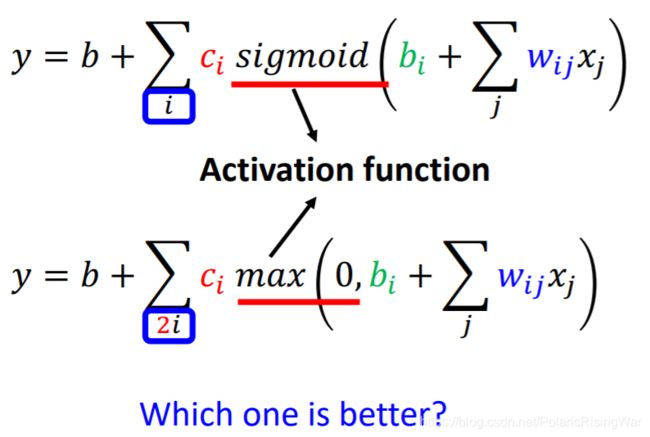 实验结果显示ReLU的效果会好一些。
实验结果显示ReLU的效果会好一些。 -
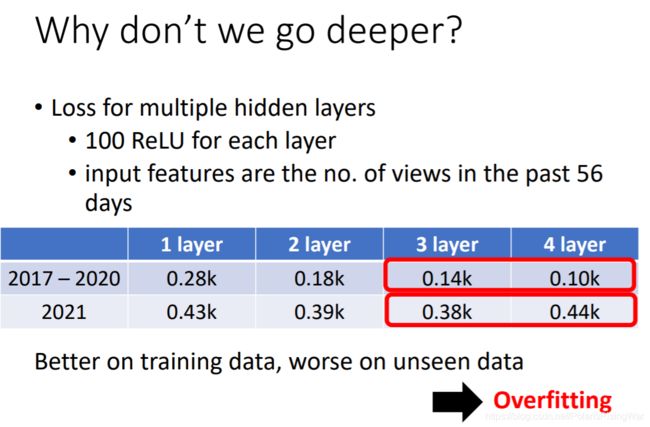
深度神经网络:很多层→实验证明加层效果会好
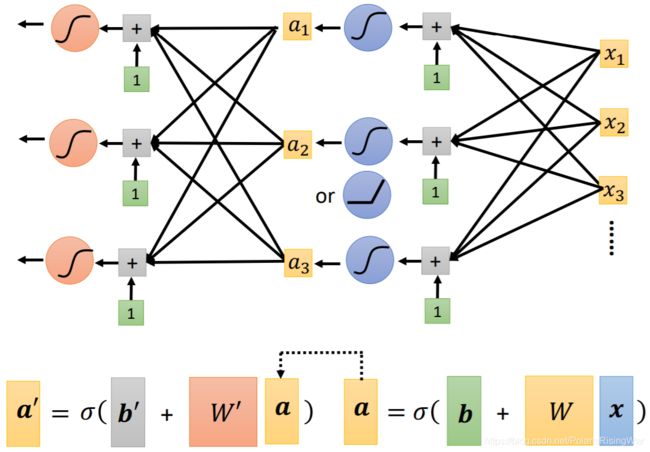
一个sigmoid就是一个neuron,很多个neuron就组成了neural network神经网络。
neuron层叫layer,输入输出之外的层叫hidden layer。
有很多层就叫deep learning。
既然很多个sigmoid或ReLU就能拟合任意函数,那么展开一层极多的神经元不就行了吗,为什么选择把网络变深而不是变胖呢?这一问题留待以后解读。
-
- 在实验中需要设定的超参:学习率,几个sigmoid(神经元的层数和个数),batch size等
2. Colab Tutorial
我自己做过注释的colab文件,已放在GitHub上:Google_Colab_Tutorial.ipynb
这部分对无法登入Google Colab的同学而言可能没必要看……
我的浏览器会直接显示中文版,所以我就截图我自己的中文版了。
- 在运行代码之前就要选择用CPU还是GPU,如果在运行过程中切换会丢掉之前所有运行结果。更换位置:


- 另需注意,免费GPU是有使用限制的,我跑了挺久的一段时间之后就遭到了制裁,不让用GPU了……
- 在代码块中用 ! 可以运行shell语句。
用 ! 开启一个新的shell,运行后就杀死进程,但是如果用 % 就会影响整个notebook进程,因此如果要运行cd(更换根目录)就要用 % 。 - notebook的根目录是临时目录,notebook运行结束就没了。这些临时文件可以下载到本地,也可以挂载谷歌云端硬盘(mounting google drive)到根目录下,挂载后对存放路径下MyDrive目录的数据修改就会实时同步到云端。
挂载代码见colab文件。也可以直接点击这个图标自动生成代码:
- Colab中常用的Linux命令行:
- ls : List all files in the current directory
- ls -l : List all files in the current directory with more detail
- pwd : Output the working directory
- mkdir : Create a directory named
- cd : Move to directory named
- gdown : Download files from google drive
- wget : Download files from the internet
- python
: Executes a python file
- 参考学习资料:开始使用Google Colaboratory(Coding TensorFlow)2
3. PyTorch Tutorial
PyTorch Tutorial分成了两部分,第一部分是中文讲的视频,主要介绍了PyTorch在一整个深度学习流程中的用法;第二部分是英文讲的视频和colab文件,主要通过 max() 及其相关函数介绍了PyTorch文档的阅读及使用技巧。
这一部分助教讲得飞快,没有基础大概是听不懂的(反正我看弹幕里很多人抱怨听不懂),在此安利我之前写的博文:60分钟闪击速成PyTorch(Deep Learning with PyTorch: A 60 Minute Blitz)学习笔记。这篇文章是PyTorch官方入门教程Deep Learning with PyTorch: A 60 Minute Blitz的笔记。这个教程很好懂,很推荐。
3.1 PyTorch Tutorial 1
- PyTorch是什么?
- 开源机器学习框架
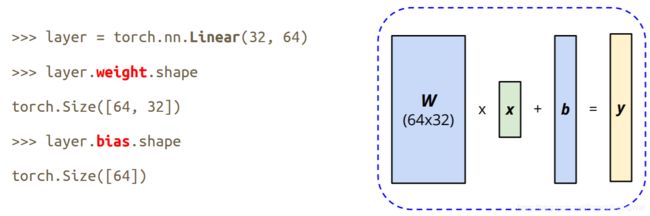
- 两大优势:支持GPU加速的张量(Tensor,类似于NumPy的array)运算,基于tape-based autograd3系统建立深度神经网络
- PyTorch v.s. TensorFlow
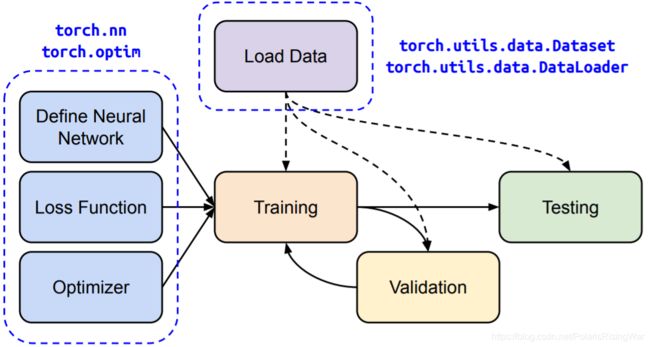
- PyTorch中深度神经网络训练流程图
- Tensor:可以视同多维数组
- 官方文档:https://pytorch.org/docs/stable/tensors.html
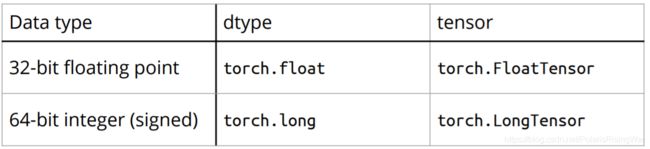
- Data Type
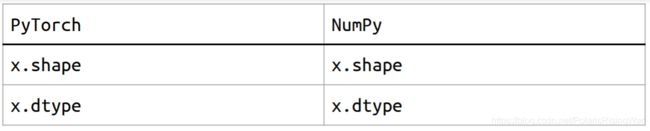
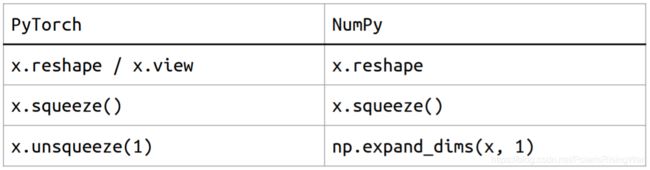
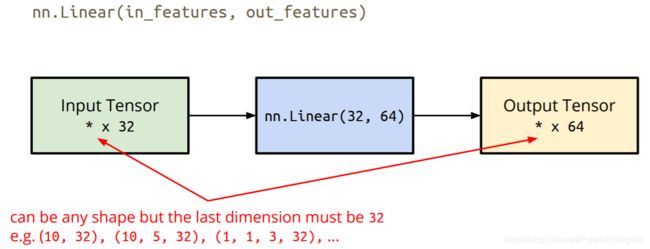
- Tensor的形状shape(维度dim)
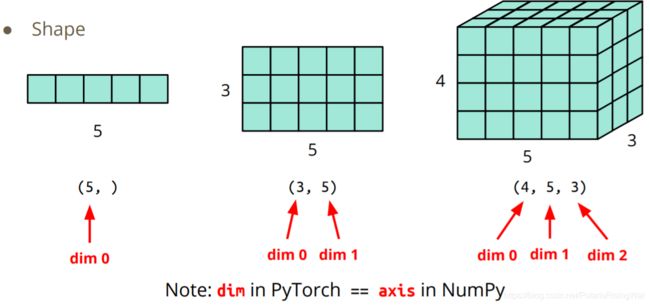
- 构造器Constructor
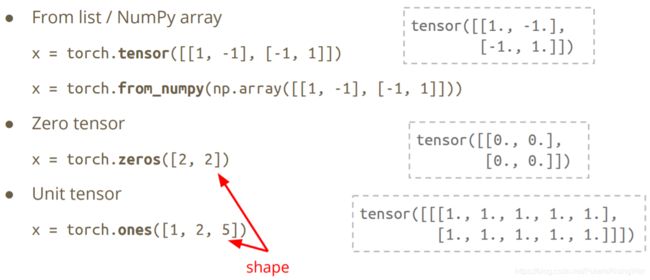
- 常用操作
- PyTorch v.s. Numpy
参考链接:https://github.com/wkentaro/pytorch-for-numpy-users - Device:Tensor和Module都默认在CPU上运行
- CPU:
x = x.to('cpu') - GPU:
x = x.to('cuda')
- CPU:
- GPU
为什么要用GPU?因为有时矩阵运算可以拆成很多小的运算,互相之间是独立的。GPU里面有很多小核心,每个小核心都可以进行小运算,全部加在一起就可以达到平行处理parallel computing,速度就会提高
检验GPU是否可用:torch.cuda.is_available()
如果有多个GPU,需要指定 ‘cuda:0’, ‘cuda:1’, ‘cuda:2’, …
对GPU的讲解可以参考towardsdatascience的这篇文章:What is a GPU and do you need one in Deep Learning?4
- 如何计算梯度?

- 创建数据集,加载数据:Dataset & Dataloader

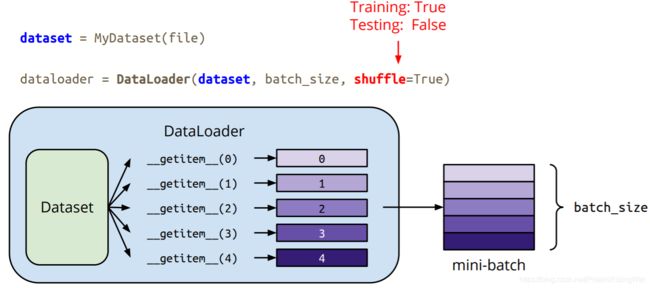 在做Testing的时候不shuffle,否则每次结果都不一样
在做Testing的时候不shuffle,否则每次结果都不一样 - 神经网络 - torch.nn
- 优化算法 - torch.optim

- 神经网络训练


10.神经网络评估(在验证集上的结果) 图中最后一行应该写在for循环外的
图中最后一行应该写在for循环外的 - 神经网络评估(测试集)

- 存储Save/下载Load神经网络模型

- 其他
- PyTorch各领域的拓展包

- 参考学习资料:
- Python教程
- w3schools的Python教程
- SoloLearn: Learn to Code
- Python官方教程
- NumPy教程:NumPy Quickstart Tutorial5
- Python教程
- 用PyTorch的实用GitHub repositories
- Huggingface Transformers (transformer models: BERT, GPT, …)
- Fairseq (sequence modeling for NLP & speech)
- ESPnet (speech recognition, translation, synthesis, …)
- Many implementation of papers
- Reference
- https://pytorch.org/
- https://github.com/pytorch/pytorch
- https://github.com/wkentaro/pytorch-for-numpy-users
- https://blog.udacity.com/2020/05/pytorch-vs-tensorflow-what-you-need-to-know.html
- https://www.tensorflow.org/
- https://numpy.org/
- PyTorch各领域的拓展包
3.2 PyTorch Tutorial 2
我自己做过注释的colab文件,已放在GitHub上:Google_Colab_Tutorial.ipynb
主要是用max()函数举例,讲了这个函数的功能,PyTorch官方文档怎么看、怎么查、怎么用,以及一些常见的PyTorch使用过程中会出现的异常。
4. HW1
4.1 任务介绍
整体任务就是用深度学习做一个回归任务,通过CMU的一组源自美国的数据来预测新冠病毒阳性案例数。
数据字段:
- id
- 自变量:40个州组成的独热编码,53个数值型变量
- 因变量:(最后一列)tested_positive.2 第3天检测为新冠病毒阳性的概率(百分比)

模型评估指标:RMSE
交作业、查看线上评估指标的kaggle网站:ML2021Spring-hw1
课程中建议可能用到的参考资料:
- Hung-yi Lee, Regression & Gradient Descent (Mandarin)
- https://www.youtube.com/watch?v=fegAeph9UaA
- https://www.youtube.com/watch?v=yKKNr-QKz2Q
- https://www.youtube.com/watch?v=1_HBTJyWgNA
- https://www.youtube.com/watch?v=wzPAInDF_gI
- https://www.youtube.com/watch?v=1UqCjFQiiy0
- https://www.youtube.com/watch?v=On1N8u1z2Ng
- Hung-yi Lee, Tips for Training Deep Networks (Mandarin)
- https://www.youtube.com/watch?v=Dr-WRlEFefw
- https://www.youtube.com/watch?v=ibJpTrp5mcE
- Google Machine Learning Crash Course (English)
- Regularization
- NN Training
4.2 simple baseline
simple baseline就是助教提供的代码,直接运行即可。
我自己做过注释的notebook文件版本放在了GitHub上:HW1_simple_baseline.ipynb。我自己跑的线上结果是private score 1.59707,public score 1.52015。
在数据预处理阶段,simple baseline提供的代码有一些问题,在下面的4.4部分我详细讲。
整体代码的逻辑如下图所示: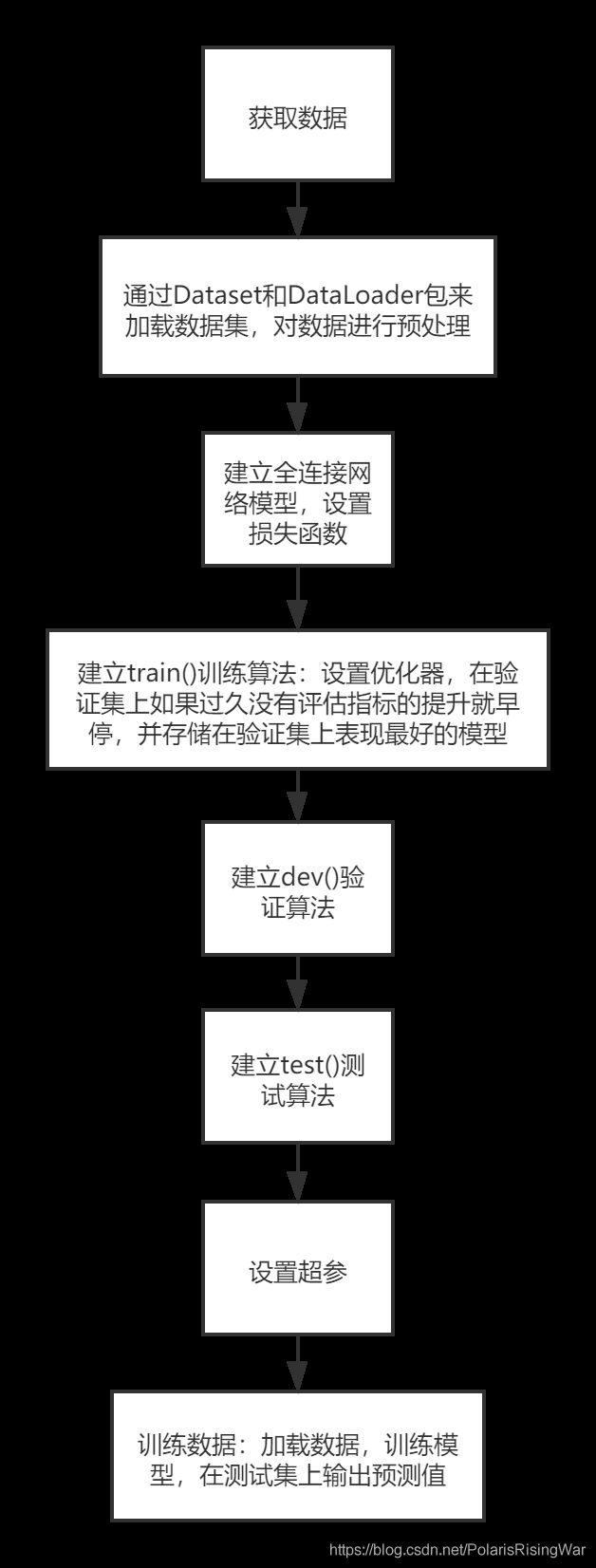
4.3 medium baseline
我写的代码已上传至GitHub:HW1_medium_baseline.ipynb
medium baseline就是把助教给的simple baseline,数据从使用全部特征改成只使用40个州和前两天测出阳性的比例这42个特征。
核心代码是将target_only这个超参调整为True,然后在Dataset部分判断target_only时,在为True的判断条件下将特征改成:
feats=list(range(40))
feats.append(57)
feats.append(75)
即可。
这样本地loss会变差,但是线上loss会提升很多。
在kaggle平台上可以看到medium baseline在private leaderboard上是1.36937,在public leaderboard上是1.28359。然后我跑出来的结果是private 1.06281,public 1.05794,满足要求。
4.4 strong baseline(我没有突破到……)
strong baseline在private leaderboard上是0.89266,在public leaderboard上是0.88017。
以下按顺序介绍调参的参考调整方向、简述我自己的调参心得、详细描述我的调参工作流程。
4.4.1 Hints
可资参考的参数调整方向(来源于助教给的notebook文件最后的cell):
- 特征选择
- DNN结构:层数,维度,激活函数
- Training:mini-batch,optimizer,learning rate
- L2 regularization
4.4.2 我的调参心得
反正我自己是没有调出来很高的参数……
从simple baseline到medium baseline就在本地loss变高,但是线上loss变低,这说明本来就已经过拟合了。这就已经导致我调参很尴尬了,因为本地loss没有参考价值了啊,它已经过拟合了啊!
但是我一开始还以为它至少总能保证本地评估指标优于线上评估指标吧,毕竟它是在本地优化的参数啊!但是medium baseline的本地loss就已经比线上loss表现更差的simple baseline要低了(不过这两个loss其实不是一个loss,本地loss是MSE,线上loss是RMSE。下面详细介绍情况),所以我就一直在试图努力优化本地loss,同时参考线上loss来调参(其实按道理讲不应该这样干的!调参应该只基于验证集,测试集只是用来参考评估模型结果的,对着测试集结果调参这种行为是不符合机器学习道义的,是不讲武德的!)。
然后我调到public score最低1.01048之后,我被colab禁用GPU了。
然后我就找找网上的公开代码,发现大家都不公开。为什么呢,明明提交时间已经截止很久了……我只找到了一个贴近strong baseline的代码:HW1_local.ipynb。我觉得这个代码写得很好,提到了很多有参考价值的内容,具体的以下讲。但是这个结果我就很震惊好吧!他把本地loss从原来的MSE调成了kaggle上用的RMSE,所以应该是同一个评估指标,但是他本地loss跑出来0.9594,线上loss跑出来0.88749,本地loss比线上loss还高!!!这数据就很他妈扯淡好吧,这根本就不科学吧!!!这还怎么调啊,这个作者是真的牛逼啊,这都能调出来!!!
如果有别的结果较好的开源代码请cue一下我,我只在kaggle那个比赛和GitHub上查了一下代码。
真的,在那一瞬间,我彻底明白了什么叫玄学,什么叫炼丹。以及我真的开始有点质疑我巧妙错过提升线上指标的参数是个什么神仙运气了,这就是玄不改非、氪不改命的深度学习版吗?我累了。
然后我就不想再认真调了,我就参考这位作者的代码来在我之前自己闭门造车瞎调参的基础上再修改修改了代码,不再不讲武德地对着测试集硬调了。但是,不知道是不是因为我脸黑,所以我测试集结果更差了……
……
……
……
在测试集上获得了更好的结果,但是违背了机器学习的道义,这值得吗?
4.4.3 详细介绍调参工作
以下首先概括性地介绍调参时使用的方法和对应效果,然后捋一下我的悲惨调参实验日志……
- 特征选择:我主要用过两种方式,一种是用相关系数,一种是sklearn的SelectKBest。
相关系数核心代码:
selected_feature_columns=[]
threshold=0.8 #阈值
#对于state列:计算斯皮尔曼系数
for i in range(40):
s_ce=train_df['tested_positive.2'].corr(train_df.iloc[:,i+1],method='spearman') #spearman coefficient
if abs(s_ce)>=threshold:
selected_feature_columns.append(i)
#对于40列后的数值型特征:计算皮尔森系数
for i in range(40,93):
p_ce=train_df['tested_positive.2'].corr(train_df.iloc[:,i]) #pearson coefficient
if abs(p_ce)>=threshold:
selected_feature_columns.append(i)
SelectKBest核心代码:
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
K=20
bestfeatures = SelectKBest(score_func=f_regression, k=K)
bestfeatures.fit(train_df.iloc[:,:-1].values,train_df.iloc[:,-1].values)
selected_feature_columns=list(bestfeatures.get_support(True))
选择参数后,在Dataset部分将feat部分代码增加 feats=list(set(feats+selected_feature_columns)) 或直接修改为 feats=selected_feature_columns 即可。
- 调整网络模型
这个直接在Module类里调就行了。但是层数一增立马就过拟合了……在网络宽度上做调整的效果也不明显。 - 修改优化器
我试了一下把优化器从SGD换成Adam,效果更差了…… - 修改划分数据集的方式
参考那篇代码。原simple baseline中使用的是分层抽样,即每10条数据中抽1条数据作为验证集,这种抽样方式可能会受到数据分布本身的影响,因此修改为通过numpy随机取样一定比例的数据作为验证集,剩下的数据作为训练集。
但是我调完以后效果反而更差了……算了。
核心代码是修改了Dataset模块划分数据集部分(rng是numpy的随机数生成器):
len_data=len(data)
len_train=int(0.7*len_data)
indices_train=list(rng.choice(len_data,len_train,replace=False))
if mode == 'train':
indices=indices_train
elif mode == 'dev':
indices=[i for i in range(len(data)) if i not in indices_train]
我在文件代码里忘写replace=False了,所以不是不放回抽样……所以我想我大约是写错了,但是我懒得改了,反正效果本来就这么差
- 修改batch_size
- 修改原simple baseline中的两处小错:参考那篇代码。
一是将损失函数从MSE改成RMSE:直接在原来的损失函数基础上再套一层torch.sqrt()即可。但是不知道为什么添加之后效果变差了很多,按道理讲应该不变啊?
二是原baseline中数据归一化是训练 / 验证 / 测试数据分别在当前数据的基础上进行归一化,但是应该按照过去数据即训练集上的均值和方差进行归一化。这一部分我看那篇代码说这么干没见着效果提升,我就懒得搞了。那篇代码上的对应核心代码:
Dataset部分:
传入mu和std参数
if self.mode == "train": #如果是训练集,均值和方差用自己数据
self.mu = self.data[:, 40:].mean(dim=0, keepdim=True)
self.std = self.data[:, 40:].std(dim=0, keepdim=True)
else: #测试集和开发集,传进来的均值和方差是来自训练集保存,如何保存均值和方差,看数据dataload部分
self.mu = mu
self.std = std
self.data[:,40:] = (self.data[:, 40:] - self.mu) / self.std #归一化
self.dim = self.data.shape[1]
DataLoader部分先加载训练集的Dataset,然后将均值和方差返回,再在加载数据时传入作为参数:
def prep_dataloader(path, mode, batch_size, n_jobs=0, target_only=False, mu=None, std=None): #训练集不需要传mu,std, 所以默认值设置为None
''' Generates a dataset, then is put into a dataloader. '''
dataset = COVID19Dataset(path, mu, std, mode=mode, target_only=target_only) # Construct dataset
if mode == 'train': #如果是训练集,把训练集上均值和方差保存下来
mu = dataset.mu
std = dataset.std
dataloader = DataLoader(
dataset, batch_size,
shuffle=(mode == 'train'), drop_last=False,
num_workers=n_jobs, pin_memory=True) # Construct dataloader
return dataloader, mu, std
在加载数据时:
tr_set, tr_mu, tr_std = prep_dataloader(tr_path, 'train', config['batch_size'], target_only=target_only)
dv_set, mu_none, std_none = prep_dataloader(tr_path, 'dev', config['batch_size'], target_only=target_only, mu=tr_mu, std=tr_std)
tt_set, mu_none, std_none = prep_dataloader(tr_path, 'test', config['batch_size'], target_only=target_only, mu=tr_mu, std=tr_std)
- L2正则化
我自己还没做到这一步的时候就被ban GPU了。后来看到那篇代码上用了L2后效果不好,我就也不想加了。
可以直接在原损失函数后面加正则化。
反正实验就跑得很心累……
我调出来最好的结果,public score达到1.01048,文件放在了GitHub上:试图冲击strong baseline,没冲过去
照着那篇靠近strong baseline的代码改了改代码结果线上loss越来越差(为什么?因为我脸黑吗?),文件也放在了GitHub上:有参考的strong baseline
实验日志是在Excel上手写的。不知道别人都是咋实现的,想搞个自动化的工具来帮我写实验日志,自己写真是越写越心累(主要是调出来效果越来越差这一点最心累,就像我写毕业论文的时候,写论文本身并不最心累,因为深知自己的论文毫无学术价值所以只能在其上屎上雕花的这种感觉最心累)。
我直接截图吧。
标红是相对于当前及之前实验,这个评估指标下最好的结果。


 以下是经代码参考后的实验:
以下是经代码参考后的实验:
可以参考我之前写过的PyTorch入门教程60分钟闪击速成PyTorch(Deep Learning with PyTorch: A 60 Minute Blitz)学习笔记 Autograd部分,就是讲自动计算微分的
↩︎这个视频就是简单讲了一些google colab怎么用的相关内容,推荐了一个类似于colab使用手册/入门手册的网页:https://colab.research.google.com/notebooks/welcome.ipynb。另外还建议使用了一个Google的AI Hub平台,我还没有去了解具体是什么
↩︎对于tape-based autograd,可以参考stackoverflow上的这个问题:What is tape-based autograd in Pytorch?
大致来说,就是有很多种自动微分方法,PyTorch中的tape-based autograd指它所使用的reverse-mode auto diff方法,可以高效计算微分,而且反向传播能用这种方法。在前向传播时autograd记录操作,在反向传播时重现操作(就像磁带一样,所以叫tape-based)。
手动更新参数时需要置required_grad为False,用torch.no_grad()实现;也可以用优化器直接自动更新参数(optimizer.step(); optimizer.zero_grad())。
与TensorFlow的对比此处不录。
↩︎对这篇文章的阅读笔记:
深度学习流程中的训练阶段是最耗资源的。
在这个阶段,更新参数和输出结果本质上都是矩阵运算。
深度神经网络可能有数以亿计的海量参数。
为了让神经网络训练更快,可以同时进行这些运算,而GPU可以做到这一点。(此处省略一些GPU本来用于图形渲染时的浮点计算工作……等介绍)
GPU比CPU小,但是有更多的logical core。
炫酷的同步运算举例视频:https://www.youtube.com/watch?v=-P28LKWTzrI(展示了用油漆喷画的过程,如果一个点一个点地喷(就像CPU),就要花好久才能喷出一幅简单的画;但是如果同时喷所有点(就像GPU),就可以非常炫酷地一步喷完蒙娜丽莎)
选择GPU还是CPU,需要考虑:
①Memory Bandwidth
②Dataset Size(如果很大大就用GPU)
③Optimization(CPU上更容易做优化)
④GPU更贵
原话:
If you consider a CPU as a Maserati, a GPU can be considered as a big truck.
The CPU (Maserati) can fetch small amounts of packages (3 - 4 passengers) in the RAM quickly whereas a GPU(the truck) is slower but can fetch large amounts of memory (~20 passengers) in one turn.
↩︎可以参考我之前写过的NumPy Quickstart Tutorial笔记 ↩︎