60分钟闪击速成PyTorch（Deep Learning with PyTorch: A 60 Minute Blitz）学习笔记

诸神缄默不语-个人CSDN博文目录

本笔记是我学习Deep Learning with PyTorch: A 60 Minute Blitz这一PyTorch官方教程后的学习笔记。
该教程在官网上更新过，因此未来还可能继续更新。以后的读者所见的版本可能与我学的不同。
以下将按照教程中四讲的顺序撰写笔记：

1. Tensor（张量）。
2. torch.autograd（自动求导包）。
3. Neural Networks（神经网络）。
4. Training a Classifier（图片分类任务示例）。

并最后整理教程中建议的衍生学习材料作为第5部分。

由于有jupyter notebook文件，因此在本文中不详细介绍代码相关的内容。对函数的解释建议翻阅PyTorch文档，也可参考我写的PyTorch Python API详解大全（持续更新ing…）一文。
文中所使用的notebook文件下载并修改自原教程。
每一节都可以点击该图标下载notebook文件：

由于原教程notebook文件中部分Markdown内容显示有问题，因此我将我下载的notebook文件上传到了GitHub公开项目Note-of-PyTorch-60-Minutes-Tutorial，这些notebook文件中的Markdown部分已经修改为了可以正常显示的形式（我是使用VSCode打开notebook文件，因此仅限于保证在VSCode中打开可以正常显示），并添加了一些我个人的学习笔记，可供参考。文件顺序见下文。
此外在该项目中还放了一个原教程中置于colab的notebook文件。详情见下文。

原教程的notebook文件基本就是网页内容本身。有条件的读者也可以直接从原教程网页跳转到colab运行代码，点击教程每页上方这个图标即可：
以后如果有缘可能会撰写colab使用方面的笔记。

建议读者提前学过线性代数和神经网络常识，会用 numpy，已经安装好 torch 和 torchvision 包

在教程首页有一个YouTube链接的视频，这只是一个两分钟的简介，没有干货，如果没有条件使用YouTube的读者也不用刻意去看。

1. Tensor

教程notebook：https://github.com/PolarisRisingWar/Note-of-PyTorch-60-Minutes-Tutorial/blob/master/tensor_tutorial.ipynb

1. 什么是Tensor？
   torch中的Tensor是一种数据结构，其实在使用上与Python的list、numpy的array、ndarray等数据结构比较类似，可以当成一个多维数组来用。
   在数学上对张量这一专业名词有特定的定义，但是反正大概理解成一个多维数组就够用了。
2. 如何生成Tensor？
   torch包中提供了一系列直接生成Tensor的函数，如zeros()、ones()、rand()等。
   此外，可以用tensor(data)函数直接将某一表示数组的数据转换为Tensor。
   也可以通过from_numpy(data)函数将numpy.ndarray格式的数据转换为Tensor。
   还可以生成一个与其他Tensor具有类似属性的Tensor，使用ones_like(data)或rand_like(data)等函数。
3. Tensor的属性：shape（返回torch.Size格式），dtype，device
4. Tensor可以进行的操作：类似numpy的API；改变原数据的原地操作在函数后面加_就可以（一般不建议这么操作）
   1. 索引
   2. 切片
   3. join：cat(tensors)或stack(tensors)
   4. 加法：add()
   5. 乘法：对元素层面的乘法mul()或*，矩阵乘法matmul()或@
5. Tensor.numpy()可以将Tensor转换为numpy数据。反向的操作见上面序号2部分。
   注意这两方向的转换的数据对象都是占用同一储存空间，修改后变化也会体现在另一对象上

2. Autograd

教程notebook：https://github.com/PolarisRisingWar/Note-of-PyTorch-60-Minutes-Tutorial/blob/master/autograd_tutorial.ipynb

1. torch.autograd是PyTorch提供的自动求导包，非常好用，可以不用自己算神经网络偏导了。
2. 神经网络构成、常识部分这里就不再详细介绍了，总之大概就是：
   1. 神经网络由权重、偏置等参数决定的函数构成，这些参数在PyTorch中都储存在Tensor里
   2. 神经网络的训练包括前向传播和反向传播两部分，前向传播就是用函数计算预测值，反向传播就是通过这一预测值产生的error/loss来更新参数（通过梯度下降的方式）
      对反向传播算法的介绍，教程中提供了3b1b的视频作为参考。原链接是YouTube视频，不方便的读者可以看B站上面的：【官方双语】深度学习之反向传播算法 上/下 Part 3 ver 0.9 beta  下篇：反向传播的微积分原理
3. 神经网络的一轮训练：
   1. 前向传播：prediction = model(data)
   2. 反向传播
      1. 计算loss
      2. loss.backward()（autograd会在这一步计算参数的梯度，存在相应参数Tensor的grad属性中）
      3. 更新参数
         1. 加载optimizer（通过torch.optim）
         2. optimizer.step()对参数使用梯度下降的方法进行更新（梯度来源自参数的grad属性）

本节以下内容都属于原理部分，可以直接跳过

4. autograd实现细节：一个示例
   1. 将Tensor的requires_grad属性设置为True，可以追踪autograd在其上每一步的操作
   2. 示例中，提供了两个requires_grad为True的Tensor（含两个元素的向量）a和b，设其损失函数$Q=3a^3-b^2$
   3. 注意：对Q计算梯度时，需要在backward()函数中添加gradient参数，这个gradient是和当前Tensor形状相同的Tensor，包含当前Tensor的梯度，比如示例中使用的是：$\frac{dQ}{dQ}=1$（因为Q是向量而非标量，参考文档。为了避免这个问题也可以直接将Q转化为标量然后使用backward()方法，如Q.sum().backward()）
   4. 计算梯度：
      external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
   5. 现在Q相对于a和b的梯度向量就分别储存在了a.grad和b.grad中，可以直接查看
5. 教程中提供了aotugrad矢量分析方面的解释，我没看懂，以后学了矢量分析看懂了再说。
6. autograd的计算图
   1. autograd维护一个由Function对象组成的DAG中的所有数据和操作。这个DAG是以输入向量为叶，输出向量为根。autograd从根溯叶计算梯度
   2. 在前向传播时，autograd同时干两件事：计算输出向量，维护DAG中操作的gradient function
   3. 反向传播以根节点调用backward()方法作为开始，autograd做以下三件事：用数据的grad_fn属性计算梯度，将梯度分别加总累积到各Tensor的grad属性中，根据链式法则传播到叶节点
   4. 如图，前序号4部分示例$Q=3a^3-b^2$的DAG（箭头是前向传播的方向，节点是前向传播过程中每个操作的backward functions，蓝色的叶节点是a和b）
      
   5. 注意：PyTorch中的DAG是动态的，每次调用backward()方法都重新填出一个DAG
7. 将Tensor的requires_grad属性设置为False，可以将其排除在DAG之外，autograd就不会计算它的梯度。
   在神经网络中，这种不需要计算梯度的参数叫frozen parameters。可以冻结不需要知道梯度的参数（节省计算资源），也可以在微调预训练模型时使用（此时往往冻结绝大多数参数，仅调整classifier layer参数，以在新标签上做预测）
   类似功能也可以用上下文管理器torch.no_grad()实现

3. Neural Networks

教程notebook：https://github.com/PolarisRisingWar/Note-of-PyTorch-60-Minutes-Tutorial/blob/master/neural_networks_tutorial.ipynb

1. 神经网络可以通过torch.nn包搭建
2. nn.Module包含了网络层
3. forward(input)方法返回输出结果
4. 示例：简单前馈神经网络convnet
   
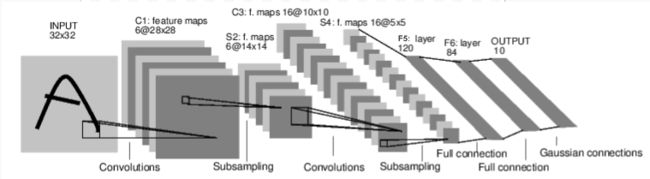
5. 典型的神经网络训练流程：（从下一序号开始对每一部分进行详细介绍）
   1. 定义具有可训练参数（或权重）的神经网络
   2. 用数据集进行多次迭代
      1. 前向传播
      2. 计算loss
      3. 计算梯度
      4. 使用梯度下降法更新参数
6. 定义网络
   只需要定义forward()方法，backward()方法会自动定义（因为用了autograd）。在forward()方法中可以进行任何Tensor操作。
   本部分代码定义了一个卷积→池化→卷积→池化→仿射变换→仿射变换→仿射变换的叠叠乐网络。
   （这个网络我有一点没搞懂，就是仿射变换前一步，既然已知数据维度是16*6*6，为什么还要用num_flat_features()这个方法算一遍啊……？）

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        #Conv2d是在输入信号（由几个平面图像构成）上应用2维卷积
        # 1 input image channel, 6 output channels, 3x3 square convolution kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        #affine仿射的
        self.fc1 = nn.Linear(16 * 6 * 6, 120)
        #16是conv2的输出通道数，6*6是图像维度
        #（32*32的原图，经conv1卷后是6*30*30，经池化后是6*15*15，经conv2卷后是16*13*13，经池化后是16*6*6）
        #经过网络层后的维度数计算方式都可以看网络的类的文档来查到
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square, you can specify with a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        #将x转化为元素不变，尺寸为[-1,self.num_flat_features(x)]的Tensor
        #-1的维度具体是多少，是根据另一维度计算出来的
        #由于另一维度是x全部特征的长度，所以这一步就是把x从三维张量拉成一维向量
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
    #计算得到x的特征总数（就是把各维度乘起来）
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

输出：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

模型的可学习参数存储在net.parameters()中。这个方法的返回值是一个迭代器，包含了模型及其所有子模型的参数

7. 前向传播：out = net(input)
8. 反向传播：先将参数梯度缓冲池清零（否则梯度会累加），再反向传播（此处使用一个随机矩阵）
   net.zero_grad()¹
   out.backward(torch.randn(1, 10))
   如果有计算出损失函数，上一行代码应为：loss.backward()
9. 注意：torch.nn只支持mini-batch，所以如果只有一个输入数据的话，可以用input.unsqueeze(0)方法创造一个伪batch维度
10. 损失函数
    torch.nn包中定义的损失函数文档：https://pytorch.org/docs/nn.html#loss-functions
    以MSELoss为例：
    criterion = nn.MSELoss()
loss = criterion(output, target)

对如此得到的loss，其grad_fn组成的DAG为：

所以，调用loss.backward()后，所有张量的梯度都会得到更新
直观举例：

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

输出：

11. 更新网络中的权重
    使用torch.optim中的优化器

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   #原因见前
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

4. CIFAR10 (Example: Image Classification)

教程notebook：https://github.com/PolarisRisingWar/Note-of-PyTorch-60-Minutes-Tutorial/blob/master/cifar10_tutorial.ipynb

1. 各种形式的数据都可以通过Python标准库转换为numpy数组格式，然后再转换为Tensor格式
   1. 图像：Pillow, OpenCV
   2. 音频：scipy and librosa
   3. 文本：raw Python or Cython based loading, or NLTK and SpaCy
2. 对计算机视觉任务，PyTorch有专门的包torchvision，可以直接通过torchvision.datasets和torch.utils.data.DataLoader下载Imagenet, CIFAR10, MNIST等常用数据集并对其进行数据转换
3. 在本教程中使用的是CIFAR10。图片是3通道，大小为32*32。标签为图像类别（共10类）
   
   

Step1：下载并规范化数据集

通过torch.utils.data.DataLoader加载torchvision.datasets中的数据集，返回迭代器
使用torchvision.transforms包进行规范化

Step2：定义一个卷积神经网络

这个神经网络和第3部分神经网络里的模型相似，只是将数据维度做了修改。
这里的数据特征尺寸在网络层之间的变化是$3\ast 32\ast 32\stackrel{(conv1)}{}6\ast 28\ast 28\stackrel{(pool)}{}6\ast 14\ast 14\stackrel{(conv2)}{}16\ast 10\ast 10\stackrel{(pool)}{}16\ast 5\ast 5\stackrel{(fc1)}{}120\stackrel{(fc2)}{}84\stackrel{(fc3)}{}10$

import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()

Step3：定义损失函数和优化器

import torch.optim as optim

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

Step4：训练神经网络

for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs; data is a list of [inputs, labels]
        inputs, labels = data

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()  
        #loss.item()文档：https://pytorch.org/docs/stable/tensors.html?highlight=item#torch.Tensor.item
        #Returns the value of this tensor as a standard Python number.
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

将模型保存到本地：

PATH = './cifar_net.pth'
torch.save(net.state_dict(), PATH)

对模型存取的更多细节详见：SERIALIZATION SEMANTICS

Step5：测试神经网络

加载模型文件：

net = Net()
net.load_state_dict(torch.load(PATH))

用测试集输出向量中最大的元素代表的类作为输出

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

在GPU上训练

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

net.to(device)
inputs, labels = data[0].to(device), data[1].to(device)  #把每一步的输入数据和目标数据也转到GPU上

多GPU数据并行训练参考教程：DATA PARALLELISM

5. 衍生学习资料

1. 微调torchvision模型教程
2. autograd具体机制
3. 逆向自动求导法应用实例 colab版 由于众所周知的有些读者可能无法登入colab，因此我也下载了原notebook文件放在了GitHub公开项目上供便捷下载，网址：https://github.com/PolarisRisingWar/Note-of-PyTorch-60-Minutes-Tutorial/blob/master/Simple_Grad.ipynb
4. 训练神经网络玩视频游戏 REINFORCEMENT LEARNING (DQN) TUTORIAL
5. 在ImageNet数据集上训练ResNet ImageNet training in PyTorch
6. 用GAN生成人脸 Deep Convolution Generative Adversarial Networks
7. 用Recurrent LSTM networks训练一个词级别的语言模型 Word-level language modeling RNN
8. 更多PyTorch应用示例
9. 更多PyTorch教程
10. 在论坛上讨论PyTorch
11. 在Slack上与其他PyTorch学习者交流

---

1. 注意这个zero_grad()方法在此处是用在了net（一个网络（nn.Module子类）实例）上，后文的zero_grad()方法则是用在了optimizer（优化器）上。
   前者的文档见https://pytorch.org/docs/stable/generated/torch.nn.Module.html#torch.nn.Module.zero_grad，是将其所有参数梯度清零。
   后者的文档见https://pytorch.org/docs/stable/optim.html#torch.optim.Optimizer.zero_grad，是将优化器上所有参数梯度清零。
   注意到我们往优化器中传的就是这个网络的所有参数：optimizer = optim.SGD(net.parameters(), lr=0.01)，所以我觉得这两种写法应该是一样的（因为model.parameters()返回一个Tensor的迭代器，Tensor作为一个可变object应该是直接传入引用，所以应该一样）。但是我还没有试验过，如果有闲情逸致的话可以试试。 ↩︎