深度学习|卷积神经网络(CNN)介绍(前篇)
01
—
回顾
以上推送了神经网络相关的介绍性内容和相关的基础理论,包括:
神经网络的基本结构:输入层,隐含层,输出层;
批随机梯度下降算法(mini-batch SGD);
前向传播,激活函数;
反向传播求参数的偏导,四个公式;
手写字数据集的mini-batch SGD 源码实现(借助BP算法求参数偏导);
对隐藏层的感性认识,神经网络的隐含层是如何从具体到抽象层层构建的。
以上阐述了深度神经网络(DNN)的基本理论,关于这些介绍请参考以下推送:
为什么要有深度学习?系统学习清单
深度学习|神经网络模型简介和梯度下降求解
深度学习|神经网络模型实现手写字分类求解思路
深度学习|神经网络模型求解思路总结
深度学习|对隐含层的感性认识
接下来,介绍下一种图像处理应用广泛的卷积神经网络算法(CNN),它是深度学习家族中非常基础且重要的算法。
02
—
为什么要有CNN?
图像处理中,往往把图像表示为像素的向量,比如一个 1000×1000 的图像,可以表示为一个10^6 的向量,就如同在手写字神经网络中,输入层为28×28 = 784 维的向量。如果隐含层的节点个数与输入层一样,即也是10^6 时,那么输入层到隐含层的参数数据为 10^6×10^6 =10^12,参数的个数太多了,要想在正常的时间内训练完,基本是不可能的。
所以要想处理1000×1000的图像分类,就得首先想办法减少参数的个数,也就是只基于深度神经网络(DNN)已经很难训练或者有没有更加优秀的算法可以专门处理这种图像分类呢? 这就是卷积神经网络,convolutional neural network ,简称为 CNN 。
03
—
图像理论预备知识
一副图像的计算机表达
在计算机中,一个二维的图像被表达为一个二维的矩阵,可以看到空白的地方取值较小,越是颜色黑的区域,矩阵对应的色素值越大。
通道(channel)
通道是一幅图像的特定组成部分,常见的手机拍出来的图片会有3个通道:红色,绿色,蓝色(RGB),也就是三通道,我们可以把它看为3个二维的数组,每一个二维数组代表一种颜色值,像素值在0~255之间。对于灰色图(grayscale),比较特殊,它仅有一个通道,如上图所示的手写字数据集中的手写字8,它就是由一个通道组成。
04
—
DNN到CNN做的改变
一般地,如下图所示为全连接的深度神经网络(DNN),每层的每个神经元节点与前层的所有神经元节点有连接,也会与后一层的所有节点相连接,这样导致的问题是每个节点都有很多个权重参数和偏置量,刚才在上文中我们提到了,那么卷积神经网络想要做的第一件事,一定是想办法解决掉这个参数多的问题吧。
CNN有几种措施可以降低参数的数目,本篇先介绍两种:第一种是局部连接(local connection),也称为局部感知,另一种是权值共享(weight sharing),下面依次介绍这两降参的方法。
局部连接
根据图像其局部的像素联系较为紧密,距离较远的像素相关性较弱,这一合理的假设,CNN认为每个神经元没有必要对整个的全局图像进行感知,只需要对局部进行感知,然后接下来的隐含层中再对局部的信息综合起来,这样就提取成了一个新的保留了原来主要特征的图像。
局部连接对权重参数的减少力度大吗? 我们来计算下,文章开始说到一个如果采用DNN,那么权重参数为10^12个,假如采取局部连接,定义隐含层的每个神经元只与输入层的100个像素建立关系,也就是说共有:10^6 × 100 个权重参数,10^8个,这个参数量还是不小吧,所以需要第二种措施,权值共享。
权值共享
上文说到,只减少隐含层的节点关联的输入层的像素点,对参数的减少力度一般,那么,在这基础上,还能做些什么呢? 如果我们再做这么一个假设:从紧邻的100个像素点抽取出一小块,并已知这一块的每个像素点的权重参数,假定这一块的权重参数也会被100个像素点的权重参数被其他块所共享,这就是权值共享,称抽取的那一小块对应的权重参数为:kernel(也可称为 filter, feature detector),并且这个操作可以一层一层地做下去,这样图像的特征会随着隐含层的加深,而逐渐变得抽象起来。
CNN借助以上两种措施对权重参数做减法,并且把这两种措施合起来,起了一个名字,叫做卷积操作,并且将这种深度学习算法称为卷积神经网络算法。
总结,可以看出,DNN中是节点与前后层是全连接的,而CNN算法对节点做了局部连接和权重参数共享,以此减少参数,加快收敛速度,使得用神经网络模型对图像进行分类操作成为了可能。
05
—
单核做卷积操作
在卷积操作中,涉及到一种特殊的操作,叫做求内积,它是两个同型矩阵对应的元素相乘,然后求和。具体说来,如下,
A和B做内积后,得到一个数:1*1 + 0*0 + 1*1 + 0*0 + 1*1 + 0*0 + 1*1 + 0*0 + 1*1 = 5,这就是两个矩阵求内积得到的结果。
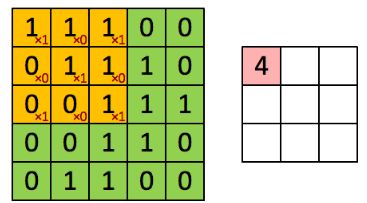
接下来,看下100个像素点,如何用一个指定大小的卷积核,做卷积操作的,为了演示的方便,直接拿一个5×5的原图像块,经过3×3的卷积核,最后如何提取特征的,首先3×3的卷积核长这样:
filter = [1 0 1
0 1 0
1 0 1 ]
为了更清晰,表达在原矩阵上,如左上角所示,这样第一次做内积后,得到 4, 放在卷积后的矩阵中的第一元素中。
第二步,要想这个filter核需要移动多大的步长呢,在此移动步长为1,这就是CNN中的一个重要超参数:步长(stride),移动1个步长和卷积操作后,得到3,再放入结果中,如下图所示:
这样依次移动9步,最后的卷积结果如下图所示:
06
—
多核做卷积操作
如果用多个卷积核进行卷积操作,应该是怎样的呢,为了表达方便,分享一个多核卷积操作的动画演示,图中的输入为 7 × 7 × 3,可以看到还做了一层零填充(Zero-padding),这是CNN中另一个重要的超参数,用到了两个过滤核:w0和w1,这在CNN中称为深度(Depth),是CNN三个超参数介绍的最后一个,分别用两个过滤核w0,和w1做了一次卷积操作,对应的得到两个卷积结果。
本gif参考网址,http://cs231n.github.io/assets/conv-demo/index.html
07
—
总结
以上这些就是CNN的卷积部分,它应用了两种技术:
局部连接
权值共享
减少了权重参数,具体这个操作为卷积操作,这个操作有3个重要的超参数:
步长(Stride)
零填充(Zero-padding)
深度(Depth)
CNN还有两部分,分别是组成CNN算法的激活函数是用了ReLU函数,当然还有池化层(pooling),明天介绍这两个块,谢谢阅读!
算法channel会有系统地,认真地推送:机器学习(包含深度学习,强化学习等)的理论,算法,实践,源码实现。期待您的参与!