leetcode 494. 目标和
目标和题解集合
- 记忆化搜索
- 动态规划
- 滚动数组优化
- 一维优化---巧妙转换为01背包问题
记忆化搜索
思路:
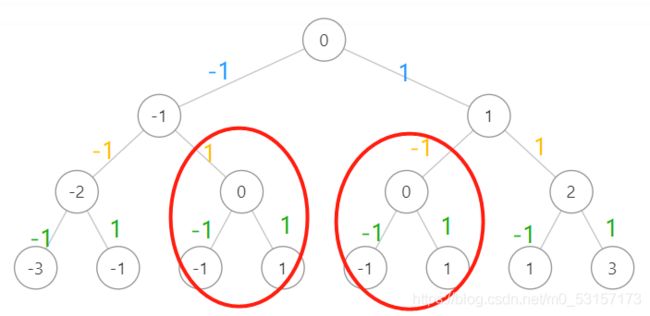
将问题转化为对一颗多叉树的遍历,而这里每个数字都有+与-的两种选择,因此这里是构造成二叉树。
看下图:
这里显然还有大量重复计算的问题,因此需要用哈希表来保存已经计算出来的结果
这里注意递归结束条件有两个:
1.所有数字都用过,并且找到和为目标值的一种方案,返回1
2.所有数字都用过,但未找到和为目标值的方案,返回0
代码:
class Solution {
unordered_map<string, int> cache;
public:
int findTargetSumWays(vector<int>& nums, int target)
{
return dfs(nums, target, 0);
}
int dfs(vector<int>& nums, int target, int index)
{
string cur = to_string(target) + "+" + to_string(index);
if (cache.find(cur) != cache.end()) return cache[cur];
if (target == 0&&index==nums.size()) return 1;
if (index >= nums.size()) return 0;
return cache[cur] = dfs(nums, target + nums[index], index + 1) + dfs(nums, target - nums[index], index + 1);
}
};
动态规划
动态规划思考过程:
1.dp[i][j]含义
考虑前i个数字的每个数字的加减与否得出当前目标值j的方案数
2.确定递推公式
搞清楚状态以后,我们就可以根据状态去考虑如何根据子问题的转移从而得到整体的解。这道题的关键不是nums[i]的选与不选,而是nums[i]是加还是减,那么我们就可以将方程定义为:
dp[i][j]=dp[i-1][j-nums[i]]+dp[i-1][j+nums[i]]
可以理解为nums[i]这个元素我可以执行加,还可以执行减,那么我dp[i][j]的结果值就是加/减之后对应位置的和。
3.dp数组初始化
什么数字都不考虑,并且当前目标值为0时,为一种方案,即dp[0][0]=1
4.确定遍历顺序
数字做外层循环,目标值做内层循环
5.举例推导dp

dp正确推导过程:
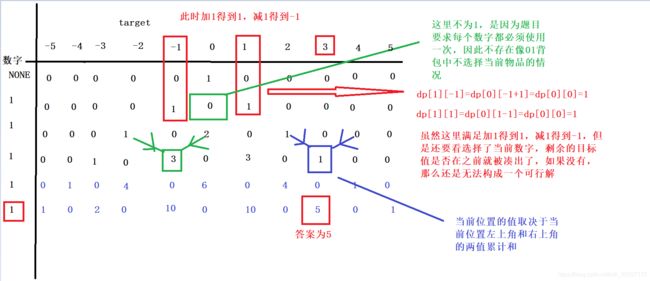
注意数组表示坐标轴需要将原点往右移动,直到所有负值变为正值
代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target)
{
int size = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
// 绝对值范围超过了sum的绝对值范围则无法得到
if (abs(target) > abs(sum)) return 0;
//注意这里列的长度
vector<vector<int>> dp(size + 1, vector<int>(2 * sum + 1,0));
int colSize = 2 * sum;
//dp数组初始化
dp[0][sum] = 1;//这里注意原点位置是sum
//考虑其他数字
for (int i = 1; i <=size; i++)
{
for (int j = 0; j <=colSize; j++)
{
// 边界
int l = (j - nums[i-1]) >= 0 ? dp[i-1][j - nums[i-1]] : 0;
int r = (j + nums[i-1]) <=colSize ? dp[i-1][j + nums[i-1]] : 0;
dp[i][j] = l + r;
}
}
return dp[size][sum+target];//这里sum就相当于原点了
}
};
滚动数组优化
因为求解当前行是需要利用上一行的数据,因此可以将行数压缩到两行,进行滚动更新。
代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target)
{
int size = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
// 绝对值范围超过了sum的绝对值范围则无法得到
if (abs(target) > abs(sum)) return 0;
//注意这里列的长度
vector<vector<int>> dp(2, vector<int>(2 * sum + 1,0));
int colSize = 2 * sum;
//dp数组初始化
dp[0][sum] = 1;//这里注意原点位置是sum
//考虑其他数字
for (int i = 1; i <=size; i++)
{
for (int j = 0; j <=colSize; j++)
{
// 边界
int l = (j - nums[i-1]) >= 0 ? dp[(i-1)&1][j - nums[i-1]] : 0;
int r = (j + nums[i-1]) <=colSize ? dp[(i-1)&1][j + nums[i-1]] : 0;
dp[i&1][j] = l + r;
}
}
return dp[size&1][sum+target];//这里sum就相当于原点了
}
};
一维优化—巧妙转换为01背包问题
因为求解当前行是需要利用上一行的数据,因此还可以抛弃数字维度,只留下目标值维度,类比01背包抛弃物品维度,留下容量维度,即变成一维数组。
但注意这里用到了前一行左上方和右上方的数据,如果从后往前覆盖,会丢失旧的右上方的数据,如果从前往后覆盖,会丢失旧的左上方的数据
因此这里如果要优化为一维数组,需要换一个思路
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = S
x = (S + sum) / 2
拿示例先解释说明一下,当要找S的时候,可以知道S是由数组中元素分成±两部分求和得来,此时把+先看做是left组合,把-看做right组合(只是分了左右组合并未真正改变其正负,最终S=left组合-right组合),这时已经得到了S=left组合-right组合,那是不是可以推出sum=left组合+right组合呢(sum是nums数组的和)?结果是肯定的,因为刚刚就是把nums分成了left组合和right组合,那加起来肯定是sum啊,接下来就要展示得到的结论了,接好了啊,来咧!!!
left组合-right组合=S
left组合+right组合=sum
left组合=(S+sum)/2;
此时我们只需要考虑从整数数组nums中选择哪几个数字相加可以得到x
此时问题就转化为,装满容量为x背包,有几种方法。
大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
因为整数相加凑不出小数
看到这种表达式,应该本能的反应,两个int相加数值可能溢出的问题,当然本题并没有溢出。
当思路转换后,就变成了01背包问题,为什么是01背包呢?
因为每个物品(题目中的1)只用一次!
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
本题则是装满有几种方法。其实这就是一个组合问题了。
1.确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[i]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
2.确定递推公式
有哪些来源可以推出dp[j]呢?
不考虑nums[i]的情况下,填满容量为j - nums[i]的背包,有dp[j - nums[i]]中方法。
那么只要搞到nums[i]的话,凑成dp[j]就有dp[j - nums[i]] 种方法。
举一个例子,nums[i] = 2,dp[3],填满背包容量为3的话,有dp[3]种方法。
那么只需要搞到一个2(nums[i]),有dp[3]方法可以凑齐容量为3的背包,相应的就有多少种方法可以凑齐容量为5的背包。
那么需要把 这些方法累加起来就可以了,dp[i] += dp[j - nums[i]]
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]
3.dp数组如何初始化
从递归公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递归结果将都是0。
dp[0] = 1,理论上也很好解释,装满容量为0的背包,有1种方法,就是装0件物品。
dp[j]其他下标对应的数值应该初始化为0,从递归公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
4.确定遍历顺序
nums放在外循环,target在内循环,且内循环倒序。
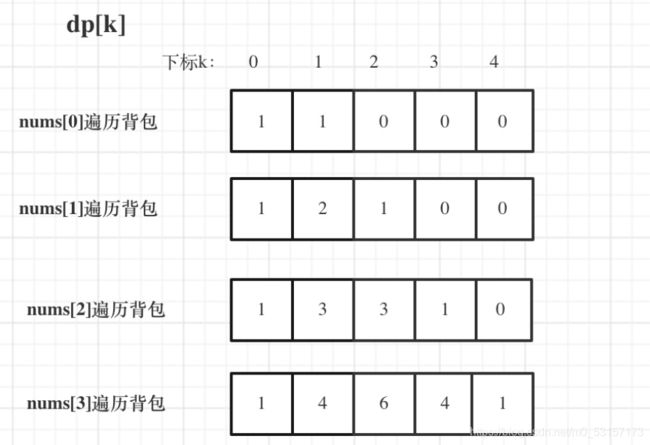
5.举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target)
{
int size = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
if ((sum + target) % 2 == 1) return 0;
// 绝对值范围超过了sum的绝对值范围则无法得到
if (abs(target) > abs(sum)) return 0;
int bagSize = (target + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < size; i++)
{
for (int j = bagSize; j >= nums[i]; j--)
dp[j] += dp[j - nums[i]];
}
return dp[bagSize];
}
};