告别加班,学会Python-Matplotlib可视化,快速完成数据分析(1)——一文详解常见统计图的绘制
告别加班,学会Python-Matplotlib可视化,快速进行数据分析(1)——一文详解常见统计图的绘制
- matplotlib库
- 曲线图
-
- 曲线图的绘制
- 结合Numpy库,绘制曲线图
- 绘制多曲线图
- 读取数据文件绘制曲线图
- 散点图
- 条形图
-
- 单组条形图
-
- 垂直条形图
- 水平条形图
- 多组条形图
- 堆积条形图
- 对称条形图
- 饼图
- 直方图
- 箱形图
- 三角网格图
matplotlib库
Matplotlib是Python的绘图库,它提供了一整套和 matlab 相似的命令 API,可以生成出版质量级别的精美图形,Matplotlib使绘图变得非常简单,在易用性和性能间取得了优异的平衡。
曲线图
曲线图的绘制
作为绘图程序的Hello World,我们将首先绘制一条简单的曲线。同时还将简单介绍matplotlib的工作原理。
# plot.py
import matplotlib.pyplot as plt
x = range(50)
y = [value * 2 for value in x]
plt.plot(x, y)
plt.show()
上述代码将会绘制曲线y=2*x,其中x在[0,50]范围内,如下所示:
 可以看到窗口上方还包含多个图标,其中:
可以看到窗口上方还包含多个图标,其中:
| 项目 | Value |
|---|---|
| 此按钮用于将所绘制的图形另存为所需格式的图片,包括png,jpg,pdf,svg等常见格式 | |
| 此按钮用于调整图片的尺寸,边距等图片属性 | |
| 此按钮用于缩放图片,用于观察图形细节,单击此按钮后,在图形上使用鼠标左键拖拽进行放大,使用鼠标右键拖拽进行缩小 | |
| 此按钮用于移动图形,可以与“缩放”按钮结合观察放大后图片的具体细节,同时,单击此按钮后,在图形上使用鼠标右键拖拽可以缩放坐标轴的比例 | |
| 此按钮用于将图形恢复到其初始状态,取消缩放、移动等操作 |
Tips:plt.plot(x, y)用于绘制一条曲线,其中,曲线点的x坐标在列表x中给出,曲线点的y坐标在列表y中给出。
由于matplotlib它只专注于绘图,因此如果想从文件中读取输入或进行一些中间计算,那么必须使用Python模块,但不用担心,matplotlib与其他模块具有良好的兼容性,并不涉及过多的技巧。例如,要生成大量统计图形,可能需要使用科学计算包,如Numpy和Python的文件读取I/O模块。在接下来的讲解中会给出相应的示例。
结合Numpy库,绘制曲线图
绘制曲线cos(x),x在[0, 2*pi]区间内:
# cos_1.py
import math
import matplotlib.pyplot as plt
scale = range(100)
x = [(2 * math.pi * i) / len(scale) for i in scale]
y = [math.cos(i) for i in x]
plt.plot(x, y)
plt.show()
若采用Numpy库,则可以使用以下等效代码:
# cos_2.py
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi, 100)
y = np.cos(x)
plt.plot(x, y)
plt.show()
所绘制图形如下所示:

Tips:虽然Numpy对于可视化而言并非必要,但可以看出使用Numpy库可以更加高效。
Numpy可以一次对整个数组执行操作,可以使代码更高效,以绘制[-10,10]区间内的曲线 y = x 3 + 5 x − 10 y=x^3+5x-10 y=x3+5x−10为例:
# plot_np.py
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 800)
y = x ** 3 + 5 * x - 10
plt.plot(x, y)
plt.show()
绘制多曲线图
很多时候我们需要对比多组数据,以发现数据间的异同,此时就需要在一张图片上绘制多条曲线——多曲线图,下图展示了在同一图片中绘制函数 y = x y=x y=x、 y = x 2 y=x^2 y=x2, y = l o g e x y=log_ex y=logex以及 y = s i n ( x ) y=sin(x) y=sin(x):
# plot_multi_curve.py
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.1, 2 * np.pi, 100)
y_1 = x
y_2 = np.square(x)
y_3 = np.log(x)
y_4 = np.sin(x)
plt.plot(x,y_1)
plt.plot(x,y_2)
plt.plot(x,y_3)
plt.plot(x,y_4)
plt.show()
Tips:一条曲线的绘制需要调用一次plt.plot(),而plt.show()只需调用一次。这种延迟呈现机制是matplotlib的核心,我们可以声明在任何时间绘制图形,但只有在调用plt.show()时才会渲染显示图形。
为了更好的说明这种延迟呈现机制,编写以下代码:
# deferred_rendering.py
import numpy as np
import matplotlib.pyplot as plt
def plot_func(x, y):
x_s = x[1:] - y[:-1]
y_s = y[1:] - x[:-1]
plt.plot(x[1:], x_s / y_s)
x = np.linspace(-5, 5, 200)
y = np.exp(-x ** 2)
plt.plot(x, y)
plot_func(x, y)
plt.show()
可以看到,尽管其中一个plt.plot()是在plot_func函数中调用的,它对图形的呈现没有任何影响,因为plt.plot()只是声明了我们要呈现的内容,但还没有执行渲染。因此可以使用此特性结合for循环、条件判断等语法完成复杂图形的绘制,同时也可以在同一张图中组合不同类型的统计图。
读取数据文件绘制曲线图
很多情况下数据都是存储于文件中,因此,需要首先读取文件中的数据,再进行绘制,说明起见,以.txt文件为例,其他诸如Excel、CSV文件可以使用pandas、numpy等库进行读取。
假设存在data.txt文件如下:
0 1
1 2
2 5
4 17
5 26
6 37
读取数据和绘制的代码如下:
# read_txt.py
import matplotlib.pyplot as plt
x, y = [], []
for line in open('data.txt', 'r'):
values = [float(s) for s in line.split()]
x.append(values[0])
y.append(values[1])
plt.plot(x, y)
plt.show()
如果使用Numpy库,其等效代码可以写为:
import matplotlib.pyplot as plt
import numpy as np
data = np.loadtxt('data.txt')
plt.plot(data[:,0], data[:,1])
plt.show()
散点图
当绘制曲线图时,我们假设点与点之间存在序列关系。而散点图是简单地绘制点,它们之间并不存在连接。
import numpy as np
import matplotlib.pyplot as plt
data = np.random.rand(1000, 2)
plt.scatter(data[:,0], data[:,1])
plt.show()

Tips:函数plt.scatter()的调用方式与plt.plot()完全相同,分别将点的x和y坐标作为输入参数。
条形图
条形图具有丰富的表现形式,常见的类型包括单组条形图,多组条形图,堆积条形图和对称条形图等。
单组条形图
条形图的每种表现形式都可以绘制成垂直条形图或水平条形图,以单组条形图的两种绘制方式为例。
垂直条形图
import matplotlib.pyplot as plt
data = [10., 20., 5., 15.]
plt.bar(range(len(data)), data)
plt.show()

Tips:plt.plot()函数的作用是:接收两个参数,包括每个条形的x坐标和每个条行的高度。
通过可选参数width,pyplot.bar()提供了一种控制条形图中条状宽度的方法:
import matplotlib.pyplot as plt
data = [10., 20., 5., 15.]
plt.bar(range(len(data)), data, width=0.5)
plt.show()
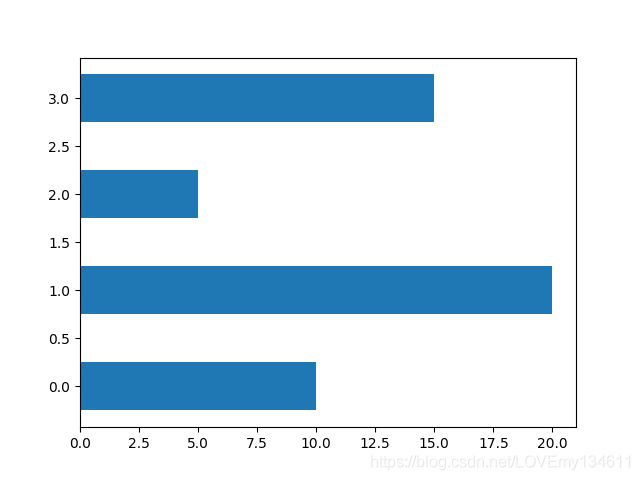
水平条形图
如果更喜欢水平条形外观,就可以使用plt.barh()函数,在用法方面与plt.bar()基本相同,但是修改条形宽度(或者在水平条形图中应该称为高度)的参数需要使用height:
import matplotlib.pyplot as plt
data = [10., 20., 5., 15.]
plt.barh(range(len(data)), data, height=0.5)
plt.show()
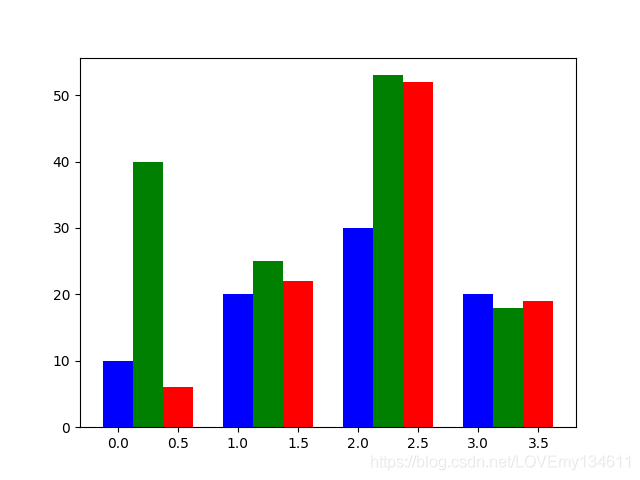
多组条形图
当需要比较不同年份相应季度的销量等此类需求时,我们可能需要多组条形图。
import numpy as np
import matplotlib.pyplot as plt
data = [[10., 20., 30., 20.],[40., 25., 53., 18.],[6., 22., 52., 19.]]
x = np.arange(4)
plt.bar(x + 0.00, data[0], color = 'b', width = 0.25)
plt.bar(x + 0.25, data[1], color = 'g', width = 0.25)
plt.bar(x + 0.50, data[2], color = 'r', width = 0.25)
plt.show()
堆积条形图
通过使用plt.bar()函数中的可选参数,可以绘制堆积条形图。
import matplotlib.pyplot as plt
y_1 = [3., 25., 45., 22.]
y_2 = [6., 25., 50., 25.]
x = range(4)
plt.bar(x, y_1, color = 'b')
plt.bar(x, y_2, color = 'r', bottom = y_1)
plt.show()

Tips:plt.bar()函数的可选参数bottom允许指定条形图的起始值。
可以结合for循环,利用延迟呈现机制堆叠更多的条形:
import numpy as np
import matplotlib.pyplot as plt
data = np.array([[5., 30., 45., 22.], [5., 25., 50., 20.], [1., 2., 1., 1.]])
x = np.arange(data.shape[1])
for i in range(data.shape[0]):
plt.bar(x, data[i], bottom = np.sum(data[:i], axis = 0))
plt.show()
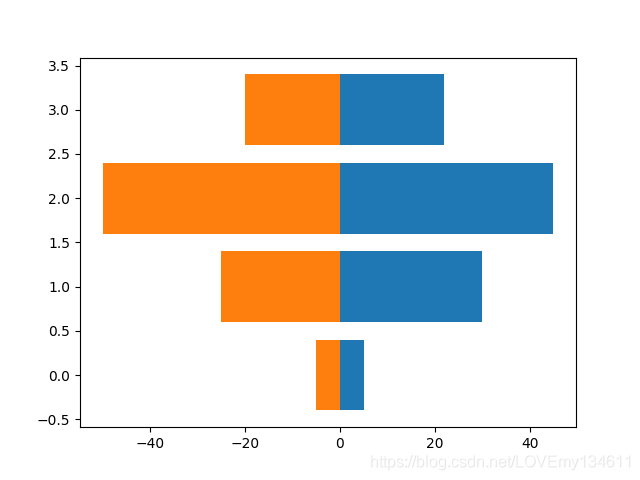
对称条形图
一个简单且有用的技巧是对称绘制两个条形图。例如想要绘制不同年龄段的男性与女性数量的对比:
import numpy as np
import matplotlib.pyplot as plt
w_pop = np.array([5., 30., 45., 22.])
m_pop = np.array( [5., 25., 50., 20.])
x = np.arange(4)
plt.barh(x, w_pop)
plt.barh(x, -m_pop)
plt.show()
图中女性人口的条形图照常绘制。然而,男性人口的条形图的条形图的条形图向左延伸,而不是向右延伸。可以使用数据的负值来快速实现对称条形图的绘制。
饼图
饼图可以用于对比数量间的相对关系:
import matplotlib.pyplot as plt
data = [10, 15, 30, 20]
plt.pie(data)
plt.show()

Tips:plt.pie()函数将一系列值作为输入,将值传递给matplolib,它就会自动计算各个值在饼图中的相对面积,并进行绘制。
直方图
直方图是概率分布的图形表示。事实上,直方图只是一种特殊的条形图。我们可以很容易地使用matplotlib的条形图函数,并进行一些统计运算来生成直方图。但是,直方图非常有用,因此matplotlib提供了一个更加方便的函数:
import numpy as np
import matplotlib.pyplot as plt
x = np.random.randn(1024)
plt.hist(x, bins = 20)
plt.show()

Tips:plt.hist()函数的作用是:获取一系列值作为输入。值的范围将被划分为大小相等的范围(默认情况下数量为10),然后生成条形图,一个范围对应一个条柱,一个条柱的高度是相应范围内中的值的数量,条柱的数量由可选参数bins确定。
箱形图
箱形图可以通过方便地显示一组值的中位数、四分位数、最大值和最小值来比较值的分布。
import numpy as np
import matplotlib.pyplot as plt
data = np.random.randn(200)
plt.boxplot(data)
plt.show()

Tips:plt.boxplot()函数的作用是:获取一组值,并自动计算平均值、中位数和其他统计量。
箱形图描述:
- 图中黄线是分布的中位数。
- 方形箱框包括从下四分位数Q1到上四分位数Q3的50%的数据。
- 下盒须的下四分位延伸到1.5(Q3-Q1)。
- 上盒须从上四分位延伸至1.5 (Q3-Q1)。
- 离盒须较远的数值用圆圈标记。
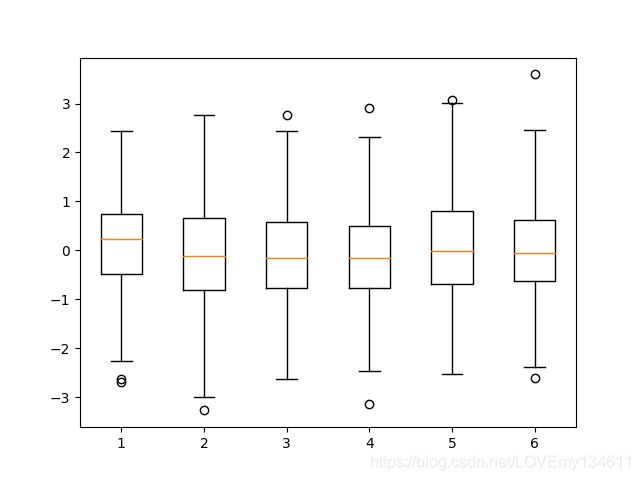
要在单个图形中绘制多个箱形图,对每个箱形图调用一次plt.boxplot()是不可行。它会将所有箱形图画在一起,形成一个混乱的、不可读的图形。如果想要到达符合要求的效果,只需在一次调用plt.boxplot()中,同时绘制多个箱形图即可,如下所示:
import numpy as np
import matplotlib.pyplot as plt
data = np.random.randn(200, 6)
plt.boxplot(data)
plt.show()
三角网格图
处理空间位置时会出现网格图。除了显示点之间的距离和邻域关系外,三角网格图也是表示地图的一种方便方法。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.tri as tri
data = np.random.rand(200, 2)
triangles = tri.Triangulation(data[:,0], data[:,1])
plt.triplot(triangles)
plt.show()