数据结构必会|图的基本概念及实现(Python)
图
1. 图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
2. 图的基本概念
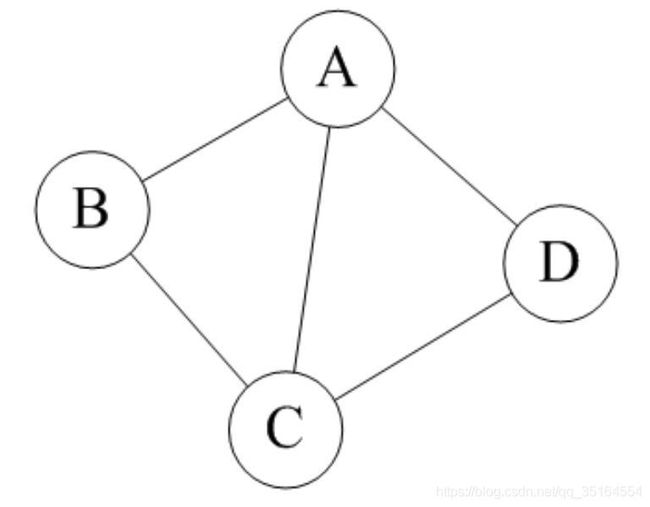
无向图
如果图中任意两个顶点之间的边都是无向边(简而言之就是没有方向的边),则称该图为无向图。
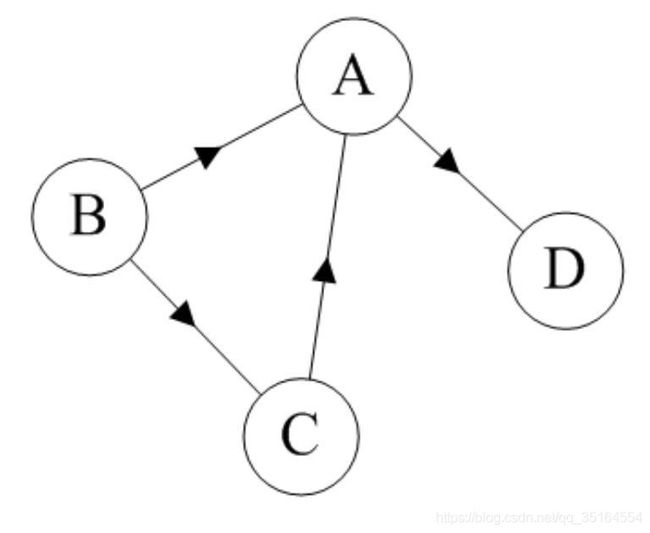
有向图
如果图中任意两个顶点之间的边都是有向边(简而言之就是有方向的边),则称该图为有向图。
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。
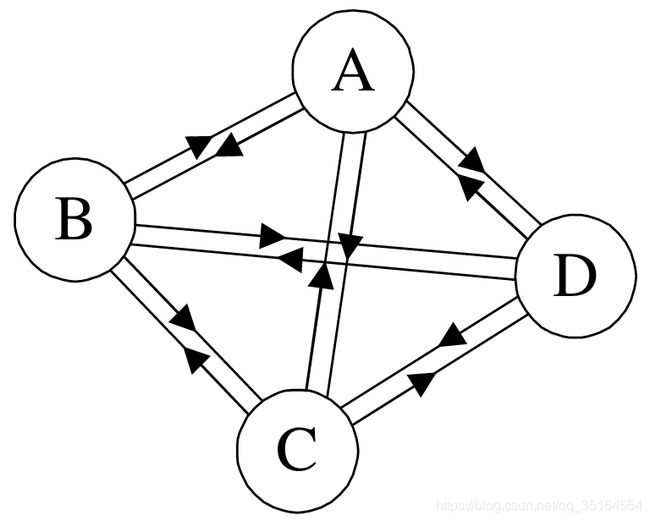
有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。
3. 图的术语
-
顶点:顶点又称为节点,是图的基础部分,我们可以给它一个名字叫“键”。
-
边:边是图的另一个基础部分,两个顶点通过一条边相连,表示它们之间存在的关系,边既可以是单向的也可以是双向的。
-
权重:边可以带权重,表示从一个顶点到另一个顶点的成本。
-
路径:路径是由边连接的顶点组成的序列。
-
环:有向图中的一条起点和终点为同一顶点的路径,没有环的图叫无环图,没有环的有向图叫有向无环图(DAG)
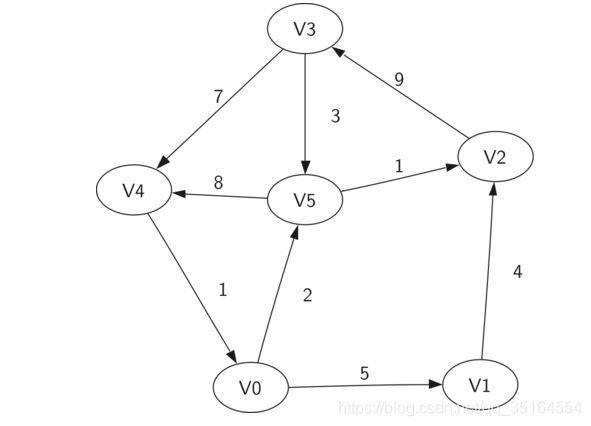
V = {V0, V1, V2, V3, V4, V5}
E = {(v0,v1,5), (v1,v2,4), (v2,v3,9), (v3,v4,7), (v4,v0,2),
(v0,v5,2), (v5,v4,8), (v3,v5,3), (v5,v2,1)}
4. 邻接矩阵
实现图最简单的方法就是邻接矩阵,在矩阵中我们用每一行每一列都表示图的一个顶点,交叉的值代表权重,示例如下:
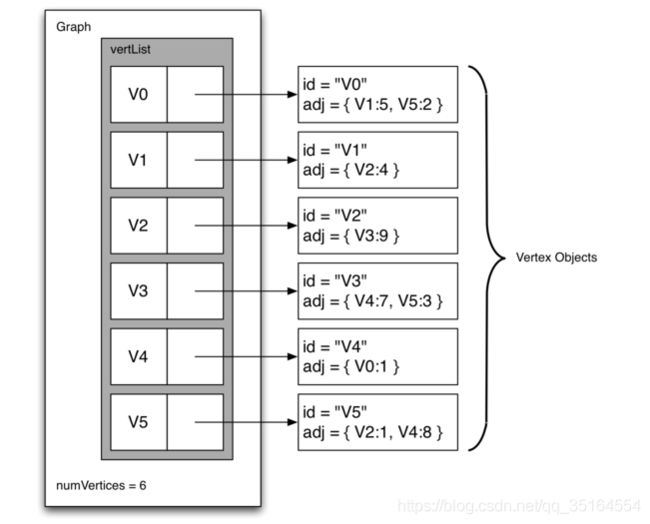
5. 邻接表
为了现稀疏连接的图,更高效的方式是使用邻接表,邻接表中我们为图对象所有的顶点保存一个主列表,同时为每一个顶点对象都维护一个列表,其中记录了与它相连的顶点。
6. 邻接表的代码实现
# 实现邻接表
class Vertex:
def __init__(self, key):
self.id = key
self.connectedTo = {
}
#从这个顶点添加一个连接到另一个
def addNeighbor(self, nbr, weight=0):
self.connectedTo[nbr] = weight
# 修改str
def __str__(self):
return str(self.id) + 'connectedTo' + str(
[x.id for x in self.connectedTo])
#返回邻接表中的所有的项点
def getConnections(self):
return self.connectedTo.keys()
def getId(self):
return self.id
#返回从这个顶点到作为参数顶点的边的权重
def getweight(self, nbr):
return self.connectedTo[nbr]
# 实现图
class Graph:
def __init__(self):
self.vertList = {
}
self.numVertices = 0
# 增加顶点
def addVertex(self, key):
self.numVertices = self.numVertices + 1
newVertex = Vertex(key)
self.vertList[key] = newVertex
return newVertex
# 返回某个顶点的信息
def getVertex(self, n):
if n in self.vertList:
return self.vertList[n]
else:
return None
# 判断顶点是否在邻接表中
def __contains__(self, n):
return n in self.vertList
# 增加边
def addEdge(self, f, t, const=0):
if f not in self.vertList:
nv = self.addVertex(f)
if t not in self.vertList:
nv = self.addVertex(t)
self.vertList[f].addNeighbor(self.vertList[t], const)
# 获取所有顶点
def getVertices(self):
return self.vertList.keys()
# 使用迭代器返回所有的邻接表信息
def __iter__(self):
return iter(self.vertList.values())
# 添加顶点
g = Graph()
for i in range(6):
g.addVertex(i)
g.vertList
# 添加边和权重
g.addEdge(0, 1, 5)
g.addEdge(0, 5, 2)
g.addEdge(1, 2, 4)
g.addEdge(2, 3, 9)
g.addEdge(3, 4, 7)
g.addEdge(3, 5, 3)
g.addEdge(4, 0, 1)
g.addEdge(5, 4, 8)
g.addEdge(5, 2, 1)
# 打印所有的边
for v in g:
# 获取所有顶点
for w in v.getConnections():
# 打印
print("( %s , %s , %s)" % (v.getId(), w.getId(), v.getweight(w)))
# 输出
'''
( 0 , 1 , 5)
( 0 , 5 , 2)
( 1 , 2 , 4)
( 2 , 3 , 9)
( 3 , 4 , 7)
( 3 , 5 , 3)
( 4 , 0 , 1)
( 5 , 4 , 8)
( 5 , 2 , 1)
'''
# 打印某个顶点的信息
print(g.getVertex(2))
print()
# 判断某个顶点是否存在(返回True和False)
print(g.__contains__(7))
print()
# 获取所有的顶点
print(g.getVertices())
print()
# 返回邻接表信息
for v in g:
print(v)
print()
for k,v in g.vertList.items():
print(k,v)
# 输出
'''
2connectedTo[3]
False
dict_keys([0, 1, 2, 3, 4, 5])
0connectedTo[1, 5]
1connectedTo[2]
2connectedTo[3]
3connectedTo[4, 5]
4connectedTo[0]
5connectedTo[4, 2]
0 0connectedTo[1, 5]
1 1connectedTo[2]
2 2connectedTo[3]
3 3connectedTo[4, 5]
4 4connectedTo[0]
5 5connectedTo[4, 2]
'''