第十二届蓝桥杯大赛软件类省赛第一场C/C++大学B组题解

A题就是一个单位换算的问题
256* 1024* 1024* 8/ 32=67108864

B题有两种方法，第一种稍微取巧一点，原理是数字1最先用完
代码：

#include
//1最先耗尽 
int main() {
   int count = 0, i;
   for(i = 0; i < 10000; i++) {
   	if(i % 10 == 1) {
   		count++;
   	}
   	if((i / 10) % 10 == 1) {
   		count++;
   	} 
   	if((i / 100) % 10 == 1) {
   		count++;
   	}
   	if((i / 1000) % 10 == 1) {
   		count++;
   	}
   	if(i / 10000 == 1) {
   		count++;
   	}
   	if(count == 2021) {
   		break;
   	}
   }
   printf("%d", i);
   return 0;
} 
//3181

当然有正规的方法，代码如下：

#include
using namespace std;
int main()
{
	int a[10],n;
	for(int i=0;i<10;i++){
		a[i]=2021;
	}
	n=1;
	while(1){
		int s=n;
		while(s){
			if(a[s%10])
				a[s%10]--;
			else
				break;
			s/=10;
		}
		if(s){
			break;
		}	
		else n++;
	}
	cout<

#include
#include
#include
using namespace std;
struct node{//点
    int x,y;
}p[1000];
struct line{//直线
    int a,b,c;//直线一般方程的系数
    bool operator<(const line &p) const {
        if (a == p.a) return b == p.b ? c < p.c : b < p.b;
        return a < p.a;
    }
    bool operator==(const line &p) const {
        return a == p.a && b == p.b && c == p.c;
    }
};
int cnt;
set se;
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int gcdd(int a,int b,int c){
    return gcd(gcd(a,b),gcd(b,c));
}
int main()
{
    int n=20,m=21;
    for(int i=0;i

核心是因式分解

#include 
using namespace std;

long long y[10000001];
int main()
{
    long long n=2021041820210418;
    long long cur=sqrt(n);
    int index=0;
    for(int i=1;i

这题有两种方法，第一种思路稍微简单一点，但是运行时间很长，代码如下：

#include 
using namespace std;

long long g[2100][2100];
int main()
{
    for(int i=1;i<2050;i++)
        for(int j=1;j<2050;j++)
            g[i][j]=1e14;
    for(int i=1;i<2050;i++)
        for(int j=i+1;j<=i+21;j++)
    {
        g[i][j]=i/__gcd(i,j)*j;
        g[j][i]=i/__gcd(i,j)*j;
    }
    for(int i=1;i<2050;i++)
        for(int j=1;j<2050;j++)
            for(int k=1;k<2050;k++)
                if((g[j][i]+g[i][k])

第二种就是很正规的迪杰斯特拉，运行速度明显更快，使用算法的优势就体现在这里

#include
using namespace std;
const int N=2510;
int g[N][N],dist[N],st[N];
int n=2021;
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int lcm(int a,int b){
    return a*b/gcd(a,b);
}
int dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;

    for(int i=1;i<=n;i++){
        int t=-1;
        for(int j=1;j<=n;j++){
            if(!st[j] && (t==-1 || dist[j]

到这里填空题才结束，不得不说一句，跟去年简直不是一个level，去年好歹我还能找规律做出蛇形填数，今年看看这数据，老老实实写代码

#include
using namespace std;
typedef long long LL;
int main()
{
    LL n;
    cin>>n;
    n/=1000;
    int h=n/3600%24;
    n=n%3600;
    int m=n/60%60;
    n=n%60;
    int s=n%60;
    printf("%02d:%02d:%02d",h,m,s);
    return 0;
}

DP解法：

#include 
#define N 102
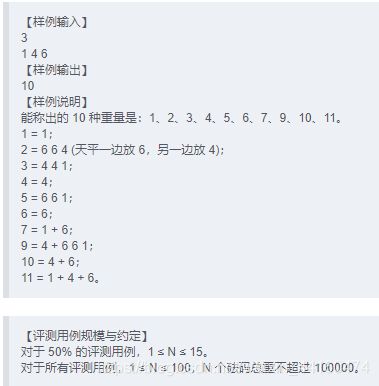
#define MAX_WEIGHT 100005
using namespace std;
int n, m, k, w[N], sum_weight, ans;
bool dp[N][MAX_WEIGHT << 2];
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &w[i]);
        sum_weight += w[i];
    }
    dp[0][sum_weight * 2] = true;
    for (int i = 1; i <= n; ++i) {
        for (int j = sum_weight; j <= sum_weight * 3; ++j) {
            dp[i][j] = dp[i][j] || dp[i - 1][j] || dp[i - 1][j - w[i]] || dp[i - 1][j + w[i]];
        }
    }
    for (int i = 1; i <= sum_weight; ++i) {
        if (dp[n][sum_weight + i] || dp[n][sum_weight - i]) {
            ++ans;
        }
    }
    printf("%d\n", ans);
    return 0;
}

大佬的题解:大佬题解链接

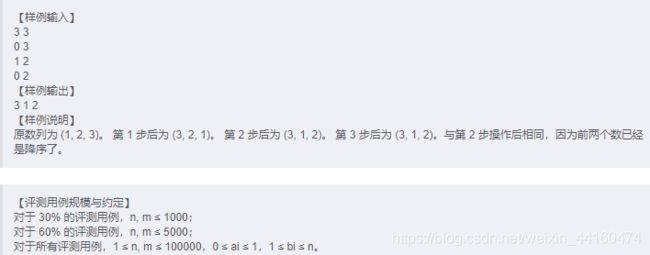
#include 
#define ll long long
#define N 100005
using namespace std;
ll n, c[N], p, q;
bool flag;
int main() {
    scanf("%lld", &n);
    if (n == 1) { //特判 1
        printf("1\n");
        return 0;
    }
    c[0] = c[1] = 1;
    p = 1;
    while (c[2] < n) {
        ++p;
        for (int i = p / 2 + 1; i > 0; --i) {
            c[i] += c[i - 1];
        }
        c[p] = 1;
        q = lower_bound(c, c + p / 2, n) - c;
        if (c[q] == n) {
            flag = true;
            break;
        }
    }
    if (flag) {
        printf("%lld\n", (1 + p) * p / 2ll + q + 1ll);
    } else {
        printf("%lld\n", (1 + n) * n / 2ll + 2ll);
    }
    return 0;
}

暂无正解，持更…


暂无正解，持更…