算法与数据结构:图的建立、遍历及其应用
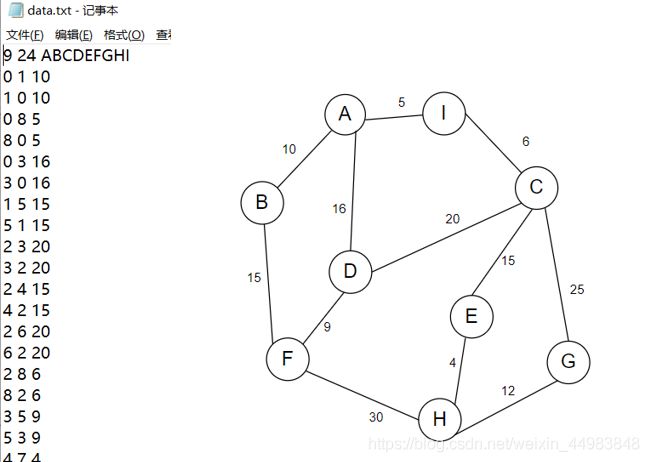
设图结点的元素类型为char,建立一个不少于8个顶点的带权无向图G,实现以下图的各种基本操作的程序:
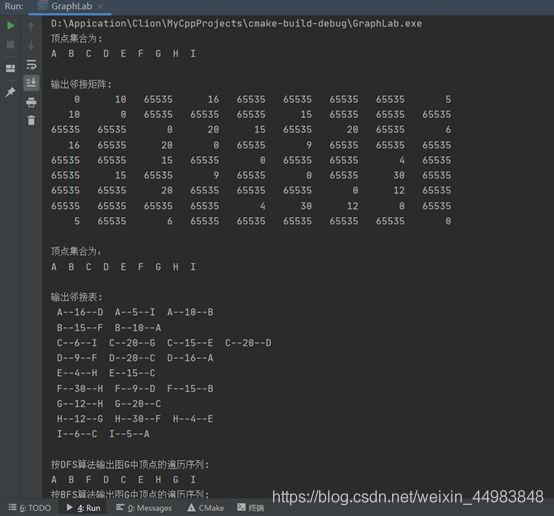
① 用邻接矩阵作为储结构存储图G并输出该邻接矩阵;
② 用邻接链表作为储结构存储图G并输出该邻接链表;
③ 按DFS算法输出图G中顶点的遍历序列;
④ 按BFS算法输出图G中顶点的遍历序列;
⑤ 用Prime算法从某个指定的顶点出发(或者Kruskal算法)输出图G的最小生成树;(要求把最小生成树的各条边输出成A-B,B-C或者(A,B,weight)的形式)
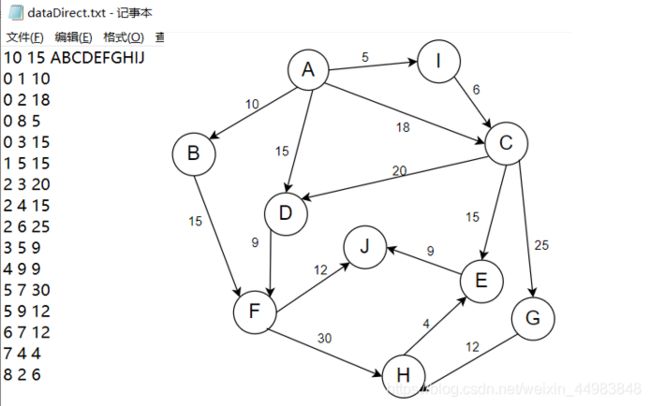
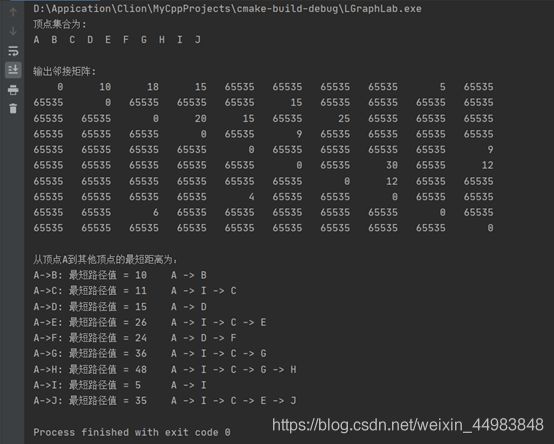
⑥ 求从有向图的某个节点出发到其余各顶点的最短路径和最短路径值;(带权有向图)
⑦ 用狄克斯特拉(Dijkastra)算法或者Floyd算法求每对顶点之间的最短路径;(带权有向图,选做)
⑧ 主函数通过函数调用实现以上各项操作。
//GraphLab.cpp
#pragma once
#include //DirectedGraph.cpp
#pragma once
#include //MatrixGraphCreate.h
#include "SeqList.h"
typedef char GDataType;
#define INF 65535 //表示无穷大
#define MaxVer 100 //最大顶点
typedef struct {
SeqList Vertices; //存放顶点
int edge[MaxVer][MaxVer];
int numOfEdges; //边数
} MGraph;
//初始化
void InitGraph(MGraph *G, int n) {
int i, j;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++) {
if (i == j)G->edge[i][j] = 0; //自己到自己权值都初始化为0
else G->edge[i][j] = INF; //所有顶点是断开的状态
}
G->numOfEdges = 0;
ListInit(&G->Vertices); //顺序表存放顶点
}
//插入顶点(图中增加一个顶点)
void InsertVer(MGraph *G, GDataType vertex) {
ListInsert(&G->Vertices, G->Vertices.size, vertex);//在表结尾插入
}
//插入边(插入一条有向边)
void InsertEdge(MGraph *G, int v1, int v2, int weight) {
if (v1 < 0 || v2 < 0 || v1 >= G->Vertices.size || v2 >= G->Vertices.size) {
printf("参数出错\n");
return;
}
G->edge[v1][v2] = weight;
G->numOfEdges++;
}
//取第一个邻接点
int GetFirstVer(MGraph G, int v) {
int col;
if (v < 0 || v > G.Vertices.size) {
printf("v越界出错\n");
return -1;
}
for (col = 0; col < G.Vertices.size; col++)
if (G.edge[v][col] > 0 && G.edge[v][col] < INF)return col;
return -1;
}
//取下一个邻接顶点
int GetNextVer(MGraph G, int v1, int v2) {
int col;
if (v1 < 0 || v2 < 0 || v1 >= G.Vertices.size || v2 >= G.Vertices.size) {
printf("参数越界出错\n");
return -1;
}
for (col = v2 + 1; col < G.Vertices.size; col++)
if (G.edge[v1][col] > 0 && G.edge[v1][col] < INF) return col;
return -1;
}
typedef struct {
int row; //行下标
int col; //列下标
int weight; //权值
} MRowColWeight; //边信息结构体
//创建图,在图G中插入n个顶点信息V和e条边信息E
void CreatGraph(MGraph *G, GDataType V[], int n, MRowColWeight E[], int e) {
int i, j;
InitGraph(G, n);
for (i = 0; i < n; i++)
InsertVer(G, V[i]); //插入顶点
for (j = 0; j < e; j++)
InsertEdge(G, E[j].row, E[j].col, E[j].weight); //插入边
}
//SeqList.h
#define Maxsize 100
typedef char LDataType;
//线性表——顺序表
typedef struct {
LDataType list[Maxsize];
int size;
} SeqList;
//初始化
void ListInit(SeqList *L) {
L->size = 0;
}
//插入数据元素
int ListInsert(SeqList *L, int i, LDataType x) {
int j;
if (L->size >= Maxsize) {
printf("顺序表已满,无法插入\n");
return 0;
} else {
for (j = L->size - 1; j > i; j--)
L->list[j] = L->list[j - 1];
L->list[i] = x;
L->size++;
return 1;
}
}
//TableGraphCreate.h
#include //Prime.h
//Prime生成最小生成树
void Prim(MGraph G, int v) {
int lowCost[MaxVer];
int closest[MaxVer];
int min, i, j, k;
for (i = 0; i < G.Vertices.size; i++) {
lowCost[i] = G.edge[v][i];
closest[i] = v;
}
for (i = 0; i < G.Vertices.size - 1; i++) {
min = INF;
k = -1;
for (j = 0; j < G.Vertices.size; j++)
if (lowCost[j] != 0 && lowCost[j] < min) {
min = lowCost[j];
k = j;
}
printf(" (%c, %c, %d)\n", G.Vertices.list[closest[k]], G.Vertices.list[k], min);
lowCost[k] = 0;
for (j = 0; j < G.Vertices.size; j++)
if (lowCost[j] != 0 && G.edge[k][j] < lowCost[j]) {
lowCost[j] = G.edge[k][j];
closest[j] = k;
}
}
}
//MGraphTraverse.h
/**visited数组记录相应顶点是否已经被访问过,0为未访问,1表示已访问*/
//图的深度优先遍历---连通图
void DFS(MGraph G, int v, int visited[]) {
int w;
printf("%c ", G.Vertices.list[v]); //访问顶点v
visited[v] = 1;
w = GetFirstVer(G, v); //取v的第一个邻接顶点
while (w != -1) {
if (!visited[w])
DFS(G, w, visited); //递归
w = GetNextVer(G, v, w);
}
}
#include "SeqQueue.h"
//广度优先搜索--连通图
void BFS(MGraph G, int v, int visited[]) {
int u, w;
SeqQueue queue;
QueueInit(&queue);
printf("%c ", G.Vertices.list[v]);//访问v顶点
visited[v] = 1;
QueueAppend(&queue, v);//初始顶点入队列
while (QueueNotEmpty(queue)) {
QueueDelete(&queue, &u);
w = GetFirstVer(G, u);
while (w != -1) {
if (!visited[w]) {
printf("%c ", G.Vertices.list[w]);
visited[w] = 1;
QueueAppend(&queue, w);
}
w = GetNextVer(G, u, w);
}
}
}
//SeqQueue.h
typedef int QDataType;
#define maxsize 100
typedef struct {
QDataType queue[maxsize];
int rear;
int front;
int count;
} SeqQueue;
//初始化
void QueueInit(SeqQueue *Q) {
Q->count = 0;
Q->front = 0;
Q->rear = 0;
}
//判断非空否
int QueueNotEmpty(SeqQueue Q) {
if (Q.count != 0) return 1;
else return 0;
}
//入队列
int QueueAppend(SeqQueue *Q, QDataType x) {
if (Q->count > 0 && Q->front == Q->rear) {
printf("队列已满\n");
return 0;
} else {
Q->queue[Q->rear] = x;
Q->rear = (Q->rear + 1) % maxsize;
Q->count++;
return 1;
}
}
//出队列
int QueueDelete(SeqQueue *Q, QDataType *x) {
if (Q->count == 0) {
printf("队列已空\n");
return 0;
} else {
*x = Q->queue[Q->front];
Q->front = (Q->front + 1) % maxsize;
Q->count--;
return 1;
}
}
//ShortestPathDjk.h
//用狄克斯特拉(Dijkastra)算法求从有向图的某个节点出发到其余各顶点的最短路径和最短路径值
void ShortestPathDjk(MGraph G, int v0, int distance[], int path[]) {
int n = G.Vertices.size;
int *s = (int *) malloc(sizeof(int) * n); //用来标记顶点是否从集合T加入集合S,加入为1,没加为0
int minDis, i, j, u;
//初始化
for (i = 0; i < n; i++) {
distance[i] = G.edge[v0][i];
s[i] = 0;
if (i != v0 && distance[i] < INF)path[i] = v0;
else path[i] = -1;
}
s[v0] = 1;
//在当前还未找到最短路径的顶点集合中,选最短路径的顶点
for (i = 1; i < n; i++) {
minDis = INF;
for (j = 0; j < n; j++)
if (s[j] == 0 && distance[j] < minDis) {
u = j;
minDis = distance[j];
}
if (minDis == INF) return;//对于非连通要加,这里连通可以不加
s[u] = 1;
//修改相应的最短距离和路径
for (j = 0; j < n; j++)
if (s[j] == 0 && (G.edge[u][j] < INF && distance[u] + G.edge[u][j] < distance[j])) {
distance[j] = distance[u] + G.edge[u][j];
path[j] = u;
}
}
}
//递归打印所有最短路径
void DisplayPath(MGraph G, int v0, int v1, int path[]) {
if (!v1)return;
DisplayPath(G, v0, path[v1], path);
printf("%c -> ", G.Vertices.list[path[v1]]);
}