Python数模笔记-NetworkX(5)关键路径法
关键路径法(Critical path method,CPM)是一种计划管理方法,通过分析项目过程中工序进度安排寻找关键路径,确定最短工期,广泛应用于系统分析和项目管理。
1、拓扑序列与关键路径
1.1 拓扑序列
一个大型工程或项目包括很多子项目,在整个项目中有些子项目没有先决条件,可以安排在任何时间开始;而有些子项目必须安排在其它子项目完成之后才能开始,也就是需要以所有前序子项目的结束为先决条件。
通过有向图可以直观反映项目中各个子项目之间的关系。图中的顶点代表活动,有向边代表活动的先后关系。有向边的起点活动是终点活动的先决条件,只有当边的起点活动完成之后,才能开始终点活动。这种以顶点表示活动、边表示活动间先后关系的有向图,称为顶点活动网(Activity on vertex network,AOV网)。
AOV网是一个有向无环图,即不存在回路。有向无环图的所有活动可排列成一个线性序列,使每个活动的所有前驱活动都排在该活动之前,称为拓扑序列(Topological order)。拓扑序列的意义是,如果按照拓扑序列中的顶点次序开始活动,每个活动开始时它的所有前驱活动都已完成,从而使整个工程得以顺序进行。
AOV网和拓扑序列只考虑网络拓结构,也就是只有各个活动的先后顺序,不考虑活动所需的时间和费用。因此,AOV网的拓扑序列通常不是唯一的,而只是各种可行顺序之一。
欢迎关注 Youcans 原创系列,每周更新数模笔记
Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法
1.2 活动网络
带权的活动网络(Activity on edge network,AOE网),顶点表示事件或状态,有向边表示活动,边上的权值通常表示活动的持续时间。AOE网可以用来估算项目的完成时间。
注意 AOV网与 AOE网的区别,不仅在于边是否带权。AOV网的顶点代表活动(工序), 边只表示先后关系;AOE网的顶点表示事件,边表示工序,边的权值表示完成工序所需的时间。
AOE 网中从起点到终点的最长的加权路径长度,称为关键路径(Critical path,CP) 。关键路径是项目中时间最长的活动顺序,决定着可能的项目最短工期 。优化关键路径可以有效地加快设工程实施的进度。
1.3 关键路径法
关键路径法(Critical path method,CPM) 是一种基于进度网络模型的方法,用网络图表示各项活动之间的相互关系,获得在一定工期、成本、资源约束条件下的最优进度安排。
关键路径法源于美国杜邦公司对于项目管理控制成本、减少工期的研究。1959年,Kelly 和 Walker 在论文 Critical Path Planning and Scheduling 中提出了关键路径法的基本原理和方法:计算所有活动的工期,确定其最早开始 ES 和最早结束 EF、最晚开始 LS 和最晚结束 LF 的时间,按照活动的相互关系形成顺序的网络逻辑 图,找到必须的最长路径即为关键路径。
关键路径法首先使用正推法(Forward pass),从起点开始向后计算,依次计算每个顶点(事件)的最早开始时间 VE;然后再使用逆推法(Backward pass),从终点开始向前计算,依次计算每个顶点(事件)的最晚开始时间 VL。在此基础上,可以进一步再求出每条边(工序)的最早开始时间 EE 和最晚开始时间 EL。最早开始时间 EE 和最晚开始时间 EL 相等的边,就是关键路径上的边,对应的工序是关键工序。
2、NetworkX 的拓扑序列和关键路径算法
NetworkX 提供了有向无环图的拓扑序列和关键路径的函数。
2.1 拓扑序列函数 topological_sort()
| 函数 | 功能 |
|---|---|
| topological_sort(DG) | 返回按拓扑排序的节点生成器 |
| all_topological_sorts(DG) | 返回所有按拓扑排序的节点生成器 |
| is_directed_acyclic_graph(DG) | 检查 DG 是否为有向无环图 |
topological_sort(DG) 返回有向无环图 DG 的一个拓扑序列,返回值的类型为
有向无环图 DG 的拓扑序列不是唯一的,all_topological_sorts(DG) 返回有向无环图 DG 的全部拓扑序列,返回值的类型为
如果 DG 不是有向图,函数抛出错误提示"NetworkXNotImplemented"。如果 DG 不是无环图,函数抛出错误提示"NetworkXUnfeasible"。
is_directed_acyclic_graph(DG) 可以检查 DG 是否为有向无环图。当 DG 为有向无环图时,返回值为 True,否则返回 False。
2.2 关键路径和路径长度函数 dag_longest_path()
| 函数 | 功能 |
|---|---|
| dag_longest_path(DG) | 返回 DG 的最长路径 |
| dag_longest_path_length(DG) | 返回 DG 的最长路径长度 |
dag_longest_path(G, weight=‘weight’, default_weight=1, topo_order=None)
dag_longest_path_length(G, weight=‘weight’, default_weight=1)
主要参数:
- G(NetworkX graph):有向无环图。
- weight (str, optional):按该字符串查找边的属性作为权重。默认值 weight=“weight”。
返回值:
- dag_longest_path() 的返回值是 DG 最长路径的顶点列表,也即关键路径的节点列表。
- dag_longest_path_length() 的返回值是 DG 最长路径的组成边的加权长度,也即关键路径的长度。
参数和返回值都非常简单,用起来是很方便的。但是,函数没有提供进行计划网络分析所需要的事件时间参数,因此也就不能在此基础上进行网络优化了。
2.3 NetworkX 使用例程
# networkX_5c.py
# Demo of critical path method(CPM) with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-05-25
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
DG = nx.DiGraph() # 创建:空的 有向图
DG.add_nodes_from(range(1, 8), VE=0, VL=0)
DG.add_weighted_edges_from([(1, 2, 5), (1, 3, 10), (1, 4, 11),
(2, 5, 4),
(3, 4, 4), (3, 5, 0),
(4, 6, 15),
(5, 6, 21), (5, 7, 25), (5, 8, 35),
(6, 7, 0), (6, 8, 20),
(7, 8, 15)])
lenNodes = len(DG.nodes) # 顶点数量
topoSeq = list(nx.topological_sort(DG)) # 拓扑序列
criticalPath = list(nx.dag_longest_path(DG)) # 关键路径(节点)
lenCriticalPath = nx.dag_longest_path_length(DG) # 关键路径的长度
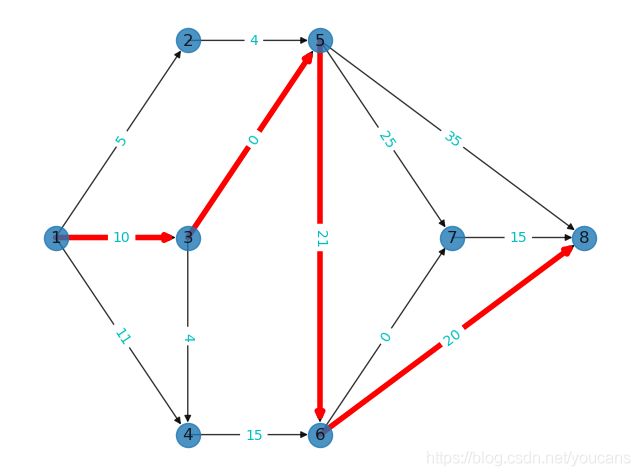
print("拓扑序列:{}".format(topoSeq)) # [1, 3, 4, 2, 5, 6, 7, 8]
print("关键路径:{}".format(criticalPath)) # [1, 3, 5, 6, 8]
print("关键路径长度:{}".format(lenCriticalPath)) # 51
pos = {
1: (0, 4), 2: (5, 8), 3: (5, 4), 4: (5, 0), 5: (10, 8), 6: (10, 0), 7: (15, 4), 8: (20, 4)} # 指定顶点位置
nx.draw(DG, pos, with_labels=True, alpha=0.8) # 绘制无向图
labels = nx.get_edge_attributes(DG, 'weight')
nx.draw_networkx_edge_labels(DG, pos, edge_labels=labels, font_color='c') # 显示边的权值
plt.show() # YouCans, XUPT
程序运行结果
拓扑序列:[1, 3, 4, 2, 5, 6, 7, 8]
关键路径:[1, 3, 5, 6, 8]
关键路径长度:51
逆转拓扑序列: [8, 7, 6, 5, 2, 4, 3, 1]
3、关键路径法案例和例程
NetworkX 虽然提供了拓扑序列和关键路径的函数,但是没有给出时间参数,如工序的最早开工时间、最晚开工时间,不能实现对计划网络图的分析和优化。
网络上关于计划网络和关键路径法的Python语言例程不多,有些并不正确或者就没有调通,有些只有部分程序不能直接使用。
作者详细研究了相关内容的 NetworkX 的说明文档,发现不少文档甚至包括官方文档也有不少问题,主要是 NetworkX 版本更新后文档不匹配。
为此,作者从拓扑序列开始,给出了关键路径算法的完整例程。为了便于阅读、使用和修改程序,本程序采用了比较简单易读的程序结构,一些地方原本是可以写的更简练的。
3.1 问题描述
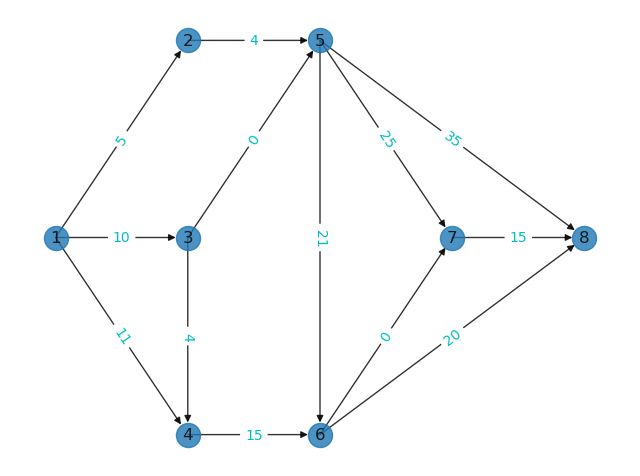
项目工程的计划网络图问题。
某项目工程由 11项作业组成(分别用 A、B、…K表示),其计划完成时间及作业间相互关系如下表所示。求:(1)完成该项目的最短时间;(2)各项目的最早开工时间、最迟开工时间和作业的关键路径。
| 作业 | 计划完成天数 | 紧前工序 | 作业 | 计划完成天数 | 紧前工序 |
|---|---|---|---|---|---|
| A | 5 | 无 | G | 21 | B,E |
| B | 10 | 无 | H | 35 | B,E |
| C | 11 | 无 | I | 25 | B,E |
| D | 4 | B | J | 15 | F,G,I |
| E | 4 | A | K | 20 | F,G |
| F | 15 | C,D |
本案例问题来自:司守奎、孙兆亮,数学建模算法与应用(第2版),P62-68,例4.16-4.18,国防工业出版社。
3.2 Python 程序
# networkX_5c.py
# Demo of critical path method(CPM) with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-05-25
# Youcans 原创作品:[Python数模笔记@Youcans](https://blog.csdn.net/youcans )
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
DG = nx.DiGraph() # 创建:空的 有向图
DG.add_nodes_from(range(1, 8), VE=0, VL=0)
DG.add_weighted_edges_from([(1, 2, 5), (1, 3, 10), (1, 4, 11),
(2, 5, 4),
(3, 4, 4), (3, 5, 0),
(4, 6, 15),
(5, 6, 21), (5, 7, 25), (5, 8, 35),
(6, 7, 0), (6, 8, 20),
(7, 8, 15)]) # 向图中添加多条赋权边: (node1,node2,weight)
lenNodes = len(DG.nodes) # 顶点数量 YouCans
topoSeq = list(nx.topological_sort(DG)) # 拓扑序列: [1, 3, 4, 2, 5, 7, 6, 8]
# --- 计算各顶点的 VE:事件最早开始时间 ---
VE = [0 for i in range(lenNodes)] # 初始化 事件最早开始时间
for i in range(lenNodes):
for e in DG.in_edges(topoSeq[i]): # 遍历顶点 topoSeq[i] 的 入边
VEij = DG.nodes[e[0]]["VE"] + DG[e[0]][e[1]]['weight'] # 该路线的最早开始时间
if VEij > VE[i]: VE[i] = VEij # 该路线所需时间更长
DG.add_node(topoSeq[i], VE=VE[i]) # 顶点(事件)的最早开始时间
# --- 计算各顶点的 VL:事件最晚开始时间 ---
revSeq = list(reversed(topoSeq)) # 翻转拓扑序列,以便从终点倒推计算 VL
VL = [DG.nodes[revSeq[0]]["VE"] for i in range(lenNodes)] # 初始化 事件最晚开始时间为 VE 最大值
for i in range(lenNodes):
for e in DG.out_edges(revSeq[i]): # 遍历顶点 revSeq[i] 的 出边
VLij = DG.nodes[e[1]]["VL"] - DG[e[0]][e[1]]['weight'] # 该路线的最晚开始时间
if VLij < VL[i]: VL[i] = VLij # 该路线所需时间更长
DG.add_node(revSeq[i], VL=VL[i]) # 顶点(事件)的最晚开始时间
print("\n顶点(事件)的最早开始时间 VE, 最晚开始时间 VL:")
for n in DG.nodes: # 遍历有向图的顶点
print("\t事件 {}:\tVE= {}\tVL= {}".format(n, DG.nodes[n]["VE"], DG.nodes[n]["VL"]))
# --- 计算各条边的 EE, EL:工序最早、最晚开始时间 ---
cpDG = nx.DiGraph() # 创建空的有向图, 保存关键路径
print("\n边(工序)的最早开始时间 EE, 最晚开始时间 EL:")
for e in DG.edges: # 遍历有向图的边
DG[e[0]][e[1]]["EE"] = DG.nodes[e[0]]["VE"] # 边的头顶点的 VE
# Wij = DG[e[0]][e[1]]['weight']
DG[e[0]][e[1]]["EL"] = DG.nodes[e[1]]["VL"] - DG[e[0]][e[1]]['weight'] # 边的尾顶点的 VL 减去边的权值
if DG[e[0]][e[1]]["EE"] == DG[e[0]][e[1]]["EL"]: # 如果最早、最晚开工时间相同,则为关键路径上的边
cpDG.add_edge(e[0], e[1], weight=DG[e[0]][e[1]]['weight']) # 加入 关键路径
print("\t工序 {}:\tEE= {}\tEL= {}".format(e, DG[e[0]][e[1]]["EE"], DG[e[0]][e[1]]["EL"]))
lenCP = sum(cpDG[e[0]][e[1]]['weight'] for e in cpDG.edges)
print("\n关键路径:{}".format(cpDG.edges)) # YouCans, XUPT
print("关键路径长度:{}".format(lenCP))
pos = {
1: (0, 4), 2: (5, 8), 3: (5, 4), 4: (5, 0), 5: (10, 8), 6: (10, 0), 7: (15, 4), 8: (20, 4)} # 指定顶点位置
nx.draw(DG, pos, with_labels=True, alpha=0.8) # 绘制无向图
labels = nx.get_edge_attributes(DG, 'weight') # YouCans, XUPT
nx.draw_networkx_edge_labels(DG, pos, edge_labels=labels, font_color='c') # 显示边的权值
nx.draw_networkx_edges(DG, pos, edgelist=cpDG.edges, edge_color='r', width=4) # 设置指定边的颜色
plt.show()
# Youcans 原创作品:[Python数模笔记@Youcans](https://blog.csdn.net/youcans )
3.3 程序说明
- AOE 图的输入。本例为稀疏的带权有向图,使用 G.add_weighted_edges_from() 函数可以使用列表向图中添加多条赋权边,每个赋权边以元组 (node1,node2,weight) 表示。
- 图中的顶点表示事件(状态),边表示问题中的作业工序,边的权值表示完成作业所需的时间。注意,(3, 5, 0),(6, 7, 0) 表示虚作业,完成该作业所需时间(资源)为0,只是表示工序的前后关系。
- nx.topological_sort(DG) 生成一个拓扑序列。
- for e in DG.in_edges(topoSeq[i]) 表示遍历顶点 topoSeq[i] 的入边,由此可以得到其所有相邻的前向顶点,各前向顶点的最早开始时间与连接边的权值之和 VEij 最大者即为该顶点的最早开始时间。顶点的最早开始时间,要从起点开始,依次向后计算,直到终点结束。
- for e in DG.out_edges(revSeq[i]) 表示遍历顶点revSeq[i] 的出边,由此可以得到其所有相邻的后向顶点,各后向顶点的最晚开始时间与连接边的权值之差 VLij 最小者即为该顶点的最晚开始时间。顶点的最晚开始时间,要从终点开始,依次向前计算,直到起点结束。
- 各条边(作业工序)的最早开始时间,是这条边的起点的最早开始时间。各条边(作业工序)的最晚开始时间,是这条边的终点的最晚开始时间减去边的权值。
- 关键路径的计算:如果一条边的最早、最晚开工时间相同,则这条边是关键路径上的边。
3.4 程序运行结果
顶点(事件)的最早开始时间 VE, 最晚开始时间 VL:
事件 1: VE= 0 VL= 0
事件 2: VE= 5 VL= 6
事件 3: VE= 10 VL= 10
事件 4: VE= 14 VL= 16
事件 5: VE= 10 VL= 10
事件 6: VE= 31 VL= 31
事件 7: VE= 35 VL= 36
事件 8: VE= 51 VL= 51
边(工序)的最早开始时间 EE, 最晚开始时间 EL:
工序 (1, 2): EE= 0 EL= 1
工序 (1, 3): EE= 0 EL= 0
工序 (1, 4): EE= 0 EL= 5
工序 (2, 5): EE= 5 EL= 6
工序 (3, 4): EE= 10 EL= 12
工序 (3, 5): EE= 10 EL= 10
工序 (4, 6): EE= 14 EL= 16
工序 (5, 6): EE= 10 EL= 10
工序 (5, 7): EE= 10 EL= 11
工序 (5, 8): EE= 10 EL= 16
工序 (6, 7): EE= 31 EL= 36
工序 (6, 8): EE= 31 EL= 31
工序 (7, 8): EE= 35 EL= 36
关键路径:[(1, 3), (3, 5), (5, 6), (6, 8)]
关键路径长度:51
版权说明:
『Youcans 原创作品』Python数模笔记@Youcans
YouCans 原创作品,转载必须标注原始链接。
Copyright 2021 YouCans, XUPT
Crated:2021-05-25
本文内容及例程为作者原创,并非转载书籍或网络内容。
本文中案例问题来自:司守奎、孙兆亮,数学建模算法与应用(第2版),国防工业出版社
欢迎关注 Youcans 原创系列,每周更新数模笔记
Python数模笔记-PuLP库(1)线性规划入门
Python数模笔记-PuLP库(2)线性规划进阶
Python数模笔记-PuLP库(3)线性规划实例
Python数模笔记-Scipy库(1)线性规划问题
Python数模笔记-StatsModels 统计回归(1)简介
Python数模笔记-StatsModels 统计回归(2)线性回归
Python数模笔记-StatsModels 统计回归(3)模型数据的准备
Python数模笔记-StatsModels 统计回归(4)可视化
Python数模笔记-Sklearn (1)介绍
Python数模笔记-Sklearn (2)聚类分析
Python数模笔记-Sklearn (3)主成分分析
Python数模笔记-Sklearn (4)线性回归
Python数模笔记-Sklearn (5)支持向量机
Python数模笔记-模拟退火算法(1)多变量函数优化
Python数模笔记-模拟退火算法(2)约束条件的处理
Python数模笔记-模拟退火算法(3)整数规划问题
Python数模笔记-模拟退火算法(4)旅行商问题
Python数模笔记-NetworkX(1)图的操作
Python数模笔记-NetworkX(2)最短路径
Python数模笔记-NetworkX(3)条件最短路径
Python数模笔记-NetworkX(4)最小生成树
Python数模笔记-NetworkX(5)关键路径法