Python机器学习应用 Unit1 聚类- K-means聚类算法 和 DBSCAN密度聚类算法
课源:Python机器学习应用 BIT嵩天,本文作为个人课堂笔记。
准备工作:导论 和 sklearn库的安装
K-means聚类算法
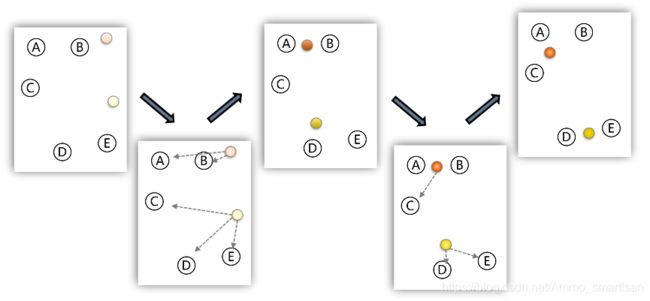
K-means算法定义/举例
**K-means聚类算法实验:
1999省份消费水平数据文件://download.csdn.net/download/Ammo_smartisan/12364455
**
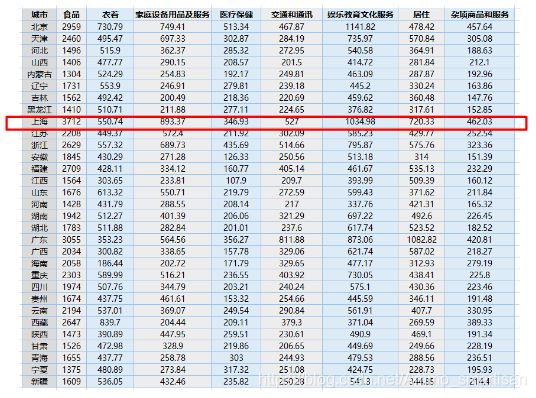
[city.txt 为1999年各个省份的消费水平在国内的情况,数据文件在资源列表下载即可。
#K-means test
import numpy as np //①建立工程,导入sklearn相关包
from sklearn.cluster import KMeans
def loadData(filePath):
fr = open(filePath,'r+') //r+ 读写打开一个文本文件
lines = fr.readlines() //依次打开整个文件
retData=[]
retCityName=[]
for line in lines:
items = line.strip().split(",")
retCityName.append(items[0]) //城市名称
retData.append([float(items[i])for i in range(1,len(items))]) //城市各项消费信息
return retData,retCityName //返回 该城市名称+消费信息
if __name__ == '__main__':
//②创建K-means算法实例并进行训练获得标签
data,cityName = loadData('city.txt') //loadData方法读取数据
km = KMeans(n_clusters = 3) //创建实例 n_clusters=聚类中心个数
label = km.fit_predict(data) //调用方法进行计算
expenses = np.sum(km.cluster_centers_,axis=1)
#print(expenses) //expenses 聚类中心数值加和=平均消费水平
CityCluster = [[],[],[]] //按照label分成设定的簇
for i in range(len(cityName)):
CityCluster[label[i]].append(cityName[i]) //输出名称
for i in range(len(CityCluster)):
print("Expenses:%2f"%expenses[i]) //输出平均花费
print(CityCluster[i])
聚成3类 n_clusters = 3 km = KMeans(n_clusters = 3) 结果:

DBSCAN密度聚类算法
DBSCAN算法定义/举例
学生上网日志数据文件://download.csdn.net/download/Ammo_smartisan/12365457


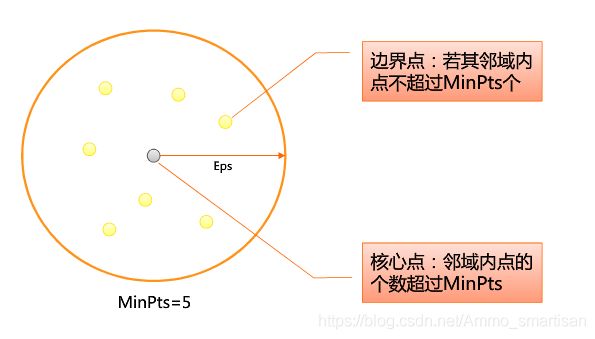
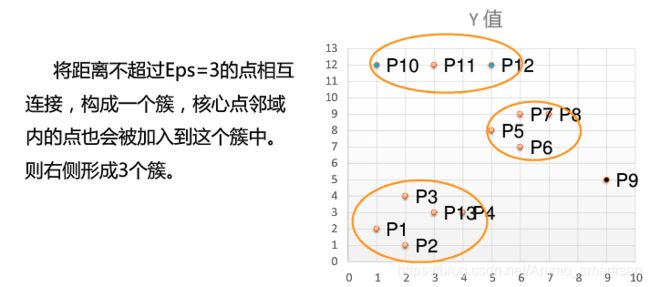
这里有两个量,一个是半径Eps,一个是指定的数目MinPts。
Eps邻域:简单来讲就是与点p的距离小于等于Eps的所有的点的集合,可以表示为NEps§)。
直接密度可达。如果p在核心对象q的Eps邻域内,则称对象p从对象q出发是直接密度可达的。
密度可达。对于对象链:p1,p2…pn,pi+1是从pi关于Eps和MinPts直接密度可达的,则对象pn是从对象p1关于Eps和MinPts密度可达的。

本博客作为个人的笔记本使用,课程参考 mooc :Python机器学习应用 。
DBSCAN聚类算法实验
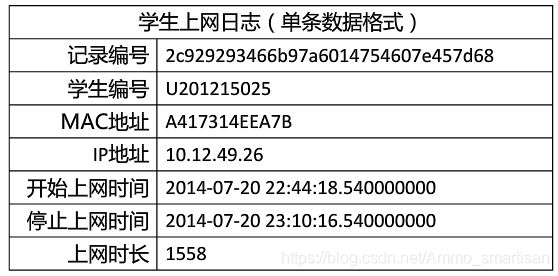
数据介绍:
现有大学校园网的日志数据, 290条大学生的校园网使用情况数据,数据包
括用户ID,设备的MAC地址,IP地址,开始上网时间,停止上网时间,上网时长,校园网套餐等。
利用已有数据,分析学生上网的模式。
实验目的:
通过DBSCAN聚类,分析学生上网时间和上网时长的模式。
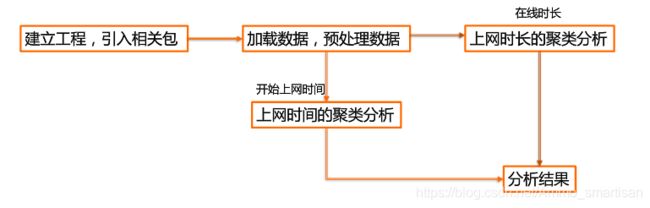
(1)按照上网时间聚类分析:
#DBSCAN_test
import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
import matplotlib.pyplot as plt
mac2id=dict()
onlinetimes=[]
f=open('TestData.txt',encoding='utf-8')
for line in f:
mac=line.split(',')[2] #读取:每条数据的MAC地址,开始上网时间和时时长
onlinetime=int(line.split(',')[6])
starttime=int(line.split(',')[4].split(' ')[1].split(':')[0])
if mac not in mac2id: #mac2id是一个字典 key=mac地址;value=时长+开始时间
mac2id[mac]=len(onlinetimes)
onlinetimes.append((starttime,onlinetime))
else:
onlinetimes[mac2id[mac]]=[(starttime,onlinetime)]
real_X=np.array(onlinetimes).reshape((-1,2))
X=real_X[:,0:1] #调用DBSCAN方法进行训练,label为每个数据的簇标签
db=skc.DBSCAN(eps=0.01,min_samples=20).fit(X)
labels = db.labels_
print('Labels:') #打印数据被记上的标签,计算标签为-1(噪声数据的比例)
print(labels)
raito=len(labels[labels[:] == -1]) / len(labels)
print('Noise raito:',format(raito, '.2%'))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) #计算簇的个数并打印
print('Estimated number of clusters: %d' % n_clusters_)
print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, labels))
for i in range(n_clusters_): #打印各簇标号及簇内数据
print('Cluster ',i,':')
print(list(X[labels == i].flatten()))
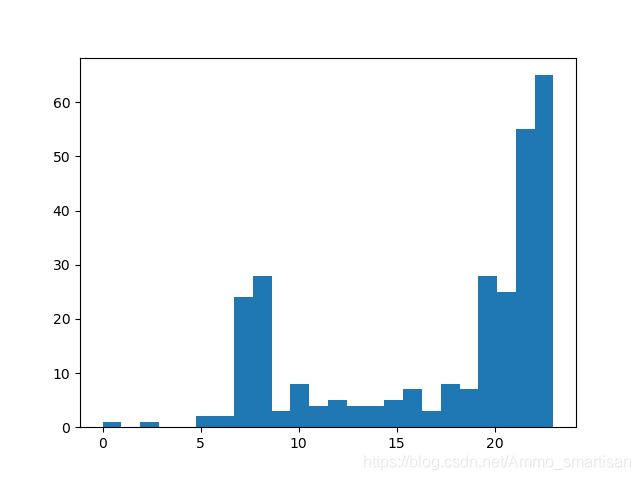
plt.hist(X,24) #转换直方图展示
运行结果:
Labels
[ 0 -1 0 1 -1 1 0 1 2 -1 1 0 1 1 3 -1 -1 3 -1 1 1 -1 1 3
4 -1 1 1 2 0 2 2 -1 0 1 0 0 0 1 3 -1 0 1 1 0 0 2 -1
1 3 1 -1 3 -1 3 0 1 1 2 3 3 -1 -1 -1 0 1 2 1 -1 3 1 1
2 3 0 1 -1 2 0 0 3 2 0 1 -1 1 3 -1 4 2 -1 -1 0 -1 3 -1
0 2 1 -1 -1 2 1 1 2 0 2 1 1 3 3 0 1 2 0 1 0 -1 1 1
3 -1 2 1 3 1 1 1 2 -1 5 -1 1 3 -1 0 1 0 0 1 -1 -1 -1 2
2 0 1 1 3 0 0 0 1 4 4 -1 -1 -1 -1 4 -1 4 4 -1 4 -1 1 2
2 3 0 1 0 -1 1 0 0 1 -1 -1 0 2 1 0 2 -1 1 1 -1 -1 0 1
1 -1 3 1 1 -1 1 1 0 0 -1 0 -1 0 0 2 -1 1 -1 1 0 -1 2 1
3 1 1 -1 1 0 0 -1 0 0 3 2 0 0 5 -1 3 2 -1 5 4 4 4 -1
5 5 -1 4 0 4 4 4 5 4 4 5 5 0 5 4 -1 4 5 5 5 1 5 5
0 5 4 4 -1 4 4 5 4 0 5 4 -1 0 5 5 5 -1 4 5 5 5 5 4
4]
Noise raito: 22.15%
Estimate number of clusters:6
Silhouette Coefficient: 0.710
Cluster 0 :
[22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22]
Cluster 1 :
[23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23]
Cluster 2 :
[20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
Cluster 3 :
[21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21]
Cluster 4 :
[8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]
Cluster 5 :
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7]
实验结果: