LeetCode题解 - 动态规划-子序列问题
LeetCode题解 - 动态规划-子序列问题
文章目录
- LeetCode题解 - 动态规划-子序列问题
-
- 参考文章:labuladong微信公众号#手把手刷动态规划系列文章#,很棒的公众号,推荐给大家
-
- 1、第一种思路模板是一个一维的 dp 数组:
- 2、第二种思路模板是一个二维的 dp 数组:
- 300. 最长递增子序列(中等)
- 646. 最长数对链(中等)
- 376. 摆动序列(中等)
- 53. 最大子序和(简单)
- 1143. 最长公共子序列(中等)
- 583. 两个字符串的删除操作(中等)
- 712. 两个字符串的最小ASCII删除和(中等)
- 72. 编辑距离(困难)
- 5. 最长回文子串(中等)
- 516. 最长回文子序列(中等)
参考文章:labuladong微信公众号#手把手刷动态规划系列文章#,很棒的公众号,推荐给大家
本文就来扒一扒子序列问题的套路,其实就有两种模板,相关问题只要往这两种思路上想,十拿九稳。
一般来说,这类问题都是让你求一个最长子序列,因为最短子序列就是一个字符嘛,没啥可问的。一旦涉及到子序列和最值,那几乎可以肯定,考察的是动态规划技巧,时间复杂度一般都是 O(n^2)。
既然要用动态规划,那就要定义 dp 数组,找状态转移关系。我们说的两种思路模板,就是 dp 数组的定义思路。不同的问题可能需要不同的 dp 数组定义来解决。
1、第一种思路模板是一个一维的 dp 数组:
int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = 最值(dp[i], dp[j] + ...)
}
}
例如在下面的例子 最长递增子序列 中,在这个思路中 dp 数组的定义是:
在子数组array[0..i]中,以array[i]结尾的目标子序列(最长递增子序列)的长度是dp[i]
2、第二种思路模板是一个二维的 dp 数组:
int n = arr.length;
int[][] dp = new dp[n][n];
for (int i = 0; i < n; i++) {
for (int j = 1; j < n; j++) {
if (arr[i] == arr[j])
dp[i][j] = dp[i][j] + ...
else
dp[i][j] = 最值(...)
}
}
这种思路运用相对更多一些,尤其是涉及两个字符串/数组的子序列。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。
2.1 涉及两个字符串/数组时(比如最长公共子序列),dp 数组的含义如下:
在子数组arr1[0..i]和子数组arr2[0..j]中,我们要求的子序列(最长公共子序列)长度为dp[i][j]。
2.2 只涉及一个字符串/数组时(比如最长回文子序列),dp 数组的含义如下:
在子数组array[i..j]中,我们要求的子序列(最长回文子序列)的长度为dp[i][j]。
300. 最长递增子序列(中等)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
输入:nums = [0,1,0,3,2,3]
输出:4
方法:动态规划(这是使用动态规划解决的一个经典问题)
明确题目中的条件:
- 子序列:不要求连续子序列,只要保证元素前后顺序一致即可;
- 上升:这里的「上升」是「严格上升」,例如:
[2, 3, 3, 6, 7]这样的子序列是不符合要求的。
题目只问最长上升子序列的长度,没有问最长上升子序列是什么,因此考虑使用动态规划。
-
状态定义:
dp[i]表示以nums[i]结尾的最长上升子序列的长度。即:在[0, ..., i]的范围内,选择以数字nums[i]结尾可以获得的最长上升子序列的长度。说明:以
nums[i]结尾,是子序列动态规划问题的经典设计状态思路,思想是动态规划的无后效性(定义得越具体,状态转移方程越好推导)。 -
推导状态转移方程:遍历到
nums[i]的时候,我们应该把下标区间[0, ... ,i - 1]的dp值都看一遍,如果当前的数nums[i]大于之前的某个数,那么nums[i]就可以接在这个数后面形成一个更长的上升子序列。把前面的数都看了,dp[i]就是它们的最大值加 1 1 1。即比当前数要小的那些里头,找最大的,然后加 1。状态转移方程即:
dp[i] = max(1 + dp[j] if j < i and nums[j] < nums[i])。 -
初始化: 单独一个数是子序列,初始化的值为 1;
-
输出: 应该扫描这个
dp数组,其中最大值的就是题目要求的最长上升子序列的长度。
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// base case:dp 数组全都初始化为 1
Arrays.fill(dp, 1);
int res = dp[0];
for(int i = 0; i < nums.length; i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
646. 最长数对链(中等)
给出 n 个数对。 在每一个数对中,第一个数字总是比第二个数字小。现在,我们定义一种跟随关系,当且仅当 b < c 时,数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。给定一个数对集合,找出能够形成的最长数对链的长度。你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
输入:[[1,2], [2,3], [3,4]]
输出:2
解释:最长的数对链是 [1,2] -> [3,4]
解题思路:与上题最长递增子序列方法类似,定义状态 dp[i] 表示以 pairs[i] 结尾的所组成的最长数对链的长度,状态转移也与上题类似, i < j 且 pairs[i][1] < pairs[j][0] 时,扩展数对链,更新 dp[j] = max(dp[j], dp[i] + 1)
重点注意:该题要求按照任意顺序选择数对都可以,为了提高效率,先把数组按照第一个元素从小到大进行排序即可;
class Solution {
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0];
}
}); //将数组对按照横坐标从小到大进行排序
int m = pairs.length;
int[] dp = new int[m];
Arrays.fill(dp, 1); //base case,对每个数组对来说,最小长度为本身即1
for(int i = 0; i < m; i++){
for(int j = 0; j < i; j++){
if(pairs[j][1] < pairs[i][0]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for(int i = 0; i < m; i++){
res= Math.max(res, dp[i]);
}
return res;
}
}
376. 摆动序列(中等)
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为**摆动序列。**第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
解题思路:每当我们选择一个元素作为摆动序列的一部分时,这个元素要么是上升的,要么是下降的,这取决于前一个元素的大小。那么列出状态表达式为:
-
up[i] 表示以前 i 个元素中的某一个为结尾的最长的「上升摆动序列」的长度
-
down[i] 表示以前 i个元素中的某一个为结尾的最长的「下降摆动序列」的长度。
最终的答案即为 up[n−1] 和 down[n−1] 中的较大值,其中 n 是序列的长度。
注意到上述方程中,我们仅需要前一个状态来进行转移,所以我们维护两个变量即可。这样我们可以写出如下的代码:
up = max(up, down + 1) down = max(up + 1, down);
注意到每有一个「峰」到「谷」的下降趋势,down 值才会增加,每有一个「谷」到「峰」的上升趋势,up 值才会增加。且过程中 down 与 up 的差的绝对值恒不大于 1,即 up ≤ down+1 且 down ≤ up+1,于是有 max(up,down+1)=down+1 且 max(up+1,down)=up+1。这样我们可以省去不必要的比较大小的过程。
参考链接
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if(n <2){
return n;
}
int up = 1, down = 1;
for(int i = 1; i < n; i++){
if(nums[i] > nums[i - 1]){
up = down + 1;
}else if(nums[i] < nums[i - 1]){
down = up + 1;
}
}
return Math.max(up, down);
}
}
53. 最大子序和(简单)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
输入:nums = [1]
输出:1
方法:动态规划(这是使用动态规划解决的一个经典问题)
明确题目中的条件:
- 连续子数组:要求必须是连续的;
-
状态定义。
dp[i]表示以nums[i]结尾的「连续子数组的最大和」。即:在[0, ..., i]的范围内,选择以数字nums[i]结尾可以获得的最大和。这种定义之下,想得到整个
nums数组的「最大子数组和」,不能直接返回dp[n-1],而需要遍历整个dp数组。 -
推导状态转移方程:
dp[i]有两种「选择」,要么与前面的相邻子数组连接,形成一个和更大的子数组;要么不与前面的子数组连接,自成一派,自己作为一个子数组。如何选择?既然要求「最大子数组和」,当然选择结果更大的那个啦:状态转移方程即:
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);。 -
初始化。单独一个数是子数组,初始化的最大和值为 nums[0];
-
输出。应该扫描这个
dp数组,其中最大值的就是题目要求的连续子数组的最大和。
class Solution {
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i = 1; i < nums.length; i++){
dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
}
int res = Integer.MIN_VALUE;
for(int i = 0; i < nums.length; i++){
res = Math.max(res, dp[i]);
}
return res;
}
}
以上解法时间复杂度是 O(N),空间复杂度也是 O(N),较暴力解法已经很优秀了,不过注意到dp[i]仅仅和dp[i-1]的状态有关,那么我们可以进行「状态压缩」,将空间复杂度降低:
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
int pre = nums[0], res = nums[0];
for(int i = 1; i < nums.length; i++){
int cur = Math.max(nums[i], pre + nums[i]);
pre = cur;
res = Math.max(res, cur);
}
return res;
}
1143. 最长公共子序列(中等)
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
解题思路:这道题为二维动态规划的经典题目。
参考链接
- 首先,区分两个概念:子序列可以是不连续的;子数组(子字符串)需要是连续的;
- 另外,动态规划也是有套路的:单个数组或者字符串要用动态规划时,可以把动态规划
dp[i]定义为nums[0:i]中想要求的结果;当两个数组或者字符串要用动态规划时,可以把动态规划定义成两维的dp[i][j],其含义是在A[0:i]与B[0:j]之间匹配得到的想要的结果。
-
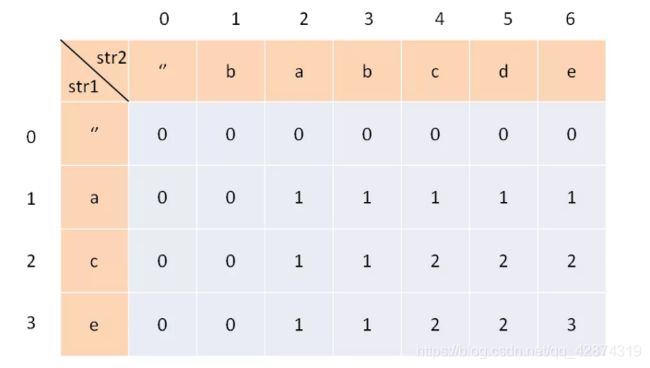
状态定义:对于本题而言,可以==定义
dp[i][j]表示text1[0:i-1]和text2[0:j-1]的最长公共子序列。==比如下图的例子,dp[2][4]的含义就是:对于"ac"和"babc",它们的 LCS 长度是 2。我们最终想得到的答案应该是dp[3][6]。(注:text1[0:i-1]表示的是text1的 第 0 个元素到第 i - 1 个元素,两端都包含)。之所以dp[i][j]的定义不是 text1[0:i]和text2[0:j],是为了方便当 i = 0 或者 j = 0 的时候,dp[i][j]表示的为空字符串和另外一个字符串的匹配,这样dp[i][j]可以初始化为 0. -
状态转移方程:
3.状态的初始化:初始化就是要看当 i = 0 与 j = 0 时, dp[i][j] 应该取值为多少。
-
当
i = 0时,dp[0][j]表示的是 text1 中取空字符串 跟 text2 的最长公共子序列,结果肯定为 0. -
当
j = 0时,dp[i][0]表示的是 text2 中取空字符串 跟 text1 的最长公共子序列,结果肯定为 0.
4.遍历方向与范围:由于 dp[i][j] 依赖与 dp[i - 1][j - 1] , dp[i - 1][j], dp[i][j - 1],所以 i 和 j 的遍历顺序肯定是从小到大的。另外,由于当 i 和 j 取值为 0 的时候,dp[i][j] = 0,而 dp 数组本身初始化就是为 0,所以,直接让 i 和 j 从 1 开始遍历。遍历的结束应该是字符串的长度为 len(text1) 和 len(text2)。
5.最终返回结果:由于 dp[i][j] 的含义是 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。我们最终希望求的是text1 和 text2 的最长公共子序列。所以需要返回的结果是 i = len(text1) 并且 j = len(text2) 时的text1 和 text2 的最长公共子序列。所以需要返回的结果是 i = len(text1) 并且 j = len(text2) 时的dp[len(text1)][len(text2)]。
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
// 定义:text1[0..i-1] 和 text2[0..j-1] 的 lcs 长度为 dp[i][j]
// 目标:text1[0..m-1] 和 text2[0..n-1] 的 lcs 长度,即 dp[m][n]
// base case: dp[0][..] = dp[..][0] = 0
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
// 现在 i 和 j 从 1 开始,所以要减一
if(text1.charAt(i - 1) == text2.charAt(j - 1)){
// text1[i-1] 和 text2[j-1] 必然在 lcs 中
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
}
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,
dp[i]表示以Si为结尾的最长递增子序列长度,子序列必须包含Si;在最长公共子序列中,dp[i][j]表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含S1i和S2j。 - 在求最终解时,最长公共子序列中
dp[N][M]就是最终解,而最长递增子序列中dp[N]不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
583. 两个字符串的删除操作(中等)
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
题目让我们计算将两个字符串变得相同的最少删除次数,那我们可以思考一下,最后这两个字符串会被删成什么样子?
删除的结果不就是它俩的最长公共子序列嘛!
那么,要计算删除的次数,就可以通过最长公共子序列的长度推导出来:
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int lenCommon = longestCommonSubsequence(word1, word2);
return m - lenCommon + n - lenCommon;
}
int longestCommonSubsequence(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
712. 两个字符串的最小ASCII删除和(中等)
给定两个字符串s1, s2,找到使两个字符串相等所需删除字符的ASCII值的最小和。
输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时,两个字符串相等,115 + 116 = 231 就是符合条件的最小和。
输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let",
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时,两个字符串都等于 "let",结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet",我们会得到 433 或 417 的结果,比答案更大。
解题思路:仍然采用上述公共子序列的解题方法,只是这道题中dp数组存储的值不是公共子序列的长度,而是他们的ASCII值的最大和。那么最后需要删除字符的ASCII值的最小和就等于两个字符串的ASCII值的总和减去公共子序列的最大和乘2。
class Solution {
public int minimumDeleteSum(String s1, String s2) {
//找到ascii码最大的公共子序列
int m = s1.length(), n = s2.length();
int total_sum = 0;
//求出两个字符串的ascii码总和
for(int i = 0; i < m; i++){
total_sum += s1.charAt(i);
}
for(int j = 0; j < n; j++){
total_sum += s2.charAt(j);
}
int[][] dp = new int[m + 1][n + 1];//补上偏移相当于给两个字符串头部加上""构造dp矩阵
//初始化矩阵
for(int i = 0; i <= m; i++){
dp[i][0] = 0;
}
for(int i = 0; i <= n; i++){
dp[0][i] = 0;
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(s1.charAt(i - 1) == s2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + s1.charAt(i - 1); //加上公共字符的ascii值
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return total_sum - 2*dp[m][n];//需要删除字符的ASCII值的最小和就等于两个字符串的ASCII值的总和减去公共子序列的最大和乘2。
}
}
72. 编辑距离(困难)
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
解题思路:解决两个字符串的动态规划问题,一般都是用两个指针i,j分别指向两个字符串的最后,然后一步步往前走,缩小问题的规模。
1.明确状态:dp[i][j] 代表 word1 中前 i 个字符,变换到 word2 中前 j 个字符,最短需要操作的次数
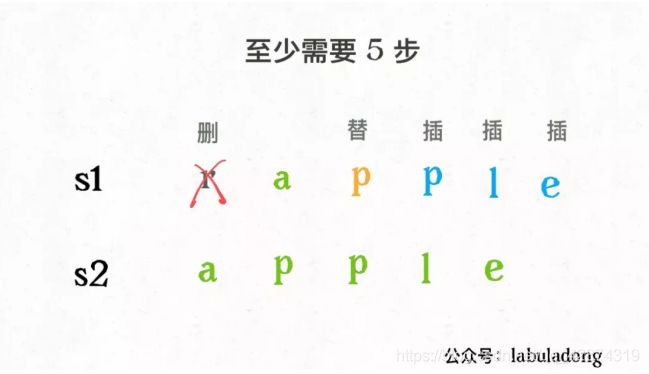
2.状态转移: 设两个字符串分别为 “rad” 和 “apple”,为了把s1变成s2,算法会这样进行:
发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
梳理思路,对于每对儿字符s1[i]和s2[j],可以有四种操作:
if s1[i] == s2[j]:
啥都别做(skip)
i, j 同时向前移动
else:
三选一: # 别忘了操作数加一
插入(insert) dp(i, j - 1) + 1 #1 直接在 s1[i] 插入一个和 s2[j] 一样的字符,那么s2[j]就被匹配了,前移 j,继续跟 i 对比
删除(delete) dp(i - 1, j) + 1 #2 直接把 s[i] 这个字符删掉,前移 i,继续跟 j 对比
替换(replace) dp(i - 1, j - 1) + 1 #3 直接把 s1[i] 替换成 s2[j],这样它俩就匹配了,同时前移 i,j 继续对比
-
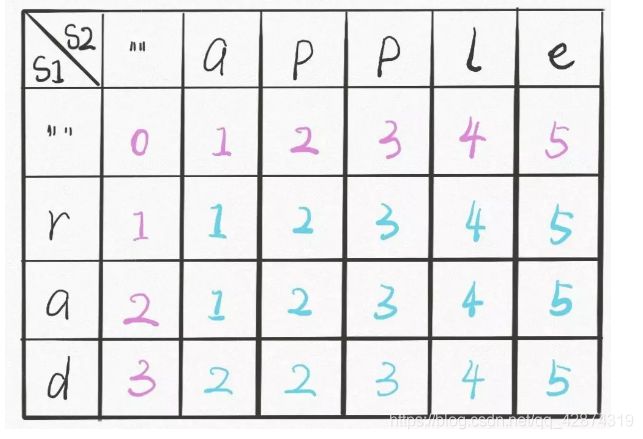
base case : 注意,针对第一行,第一列要单独考虑,我们引入
''下图所示:第一行,是word1为空变成word2最少步数,就是插入操作;第一列,是word2为空,需要的最少步数,就是删除操作。这两种情况就是算法的 base case。
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m +1][n + 1];
//base case
for(int i = 1; i <= m; i++){
dp[i][0] = i;
}
for(int j = 1; j <= n; j++){
dp[0][j] = j;
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1.charAt(i-1) == word2.charAt(j - 1)){
dp[i][j] = dp[i -1][j - 1];
}else{
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
);
}
}
}
return dp[m][n];
}
int min(int a, int b, int c){
return Math.min(a, Math.min(b, c));
}
}
5. 最长回文子串(中等)
给你一个字符串 s,找到 s 中最长的回文子串。
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
输入:s = "cbbd"
输出:"bb"
解题思路:解决该类问题的核心是双指针。寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串。但是呢,由于回文串的长度可能是奇数也可能是偶数,所以
for 0 <= i < len(s):
# 找到以 s[i] 为中心的回文串
palindrome(s, i, i)
# 找到以 s[i] 和 s[i+1] 为中心的回文串
palindrome(s, i, i + 1)
更新答案
class Solution {
public String longestPalindrome(String s) {
//记录最长回文子串
String res = "";
// 穷举以所有点(奇数一个点,偶数两个点)为中心的回文串
for(int i = 0; i < s.length(); i++){
// 当回文串是奇数时,由一个中心点向两边扩散
String s1 = palindrome(s, i, i);
// 当回文串是偶数时,由中间的两个中心点向两边扩散
String s2 = palindrome(s, i, i+1);
res = res.length() > s1.length() ? res : s1;
res = res.length() > s2.length() ? res : s2;
}
return res;
}
// 辅助函数:寻找回文串
public String palindrome(String s, int left, int right){
// 在区间 [0, s.length() - 1] 中寻找回文串,防止下标越界
while(left >= 0 && right < s.length()){
if(s.charAt(left) == s.charAt(right)){
// 是回文串时,继续向两边扩散
left --;
right ++;
}else{
break;
}
}
// 循环结束时的条件是 s.charAt(left) != s.charAt(right), 所以正确的区间为 [left + 1, right), 方法 substring(start, end) 区间是 [start, end), 不包含 end
return s.substring(left + 1, right);
}
}
至此,这道最长回文子串的问题就解决了,时间复杂度 O(N^2),空间复杂度 O(1)。
值得一提的是,这个问题可以用动态规划方法解决,时间复杂度一样,但是空间复杂度至少要 O(N^2) 来存储 DP table。这道题是少有的动态规划非最优解法的问题。
516. 最长回文子序列(中等)
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb"。
解题思路:这个问题对 dp 数组的定义是:在子串s[i..j]中,最长回文子序列的长度为dp[i][j]。一定要记住这个定义才能理解算法。
为啥这个问题要这样定义二维的 dp 数组呢?具体来说,如果我们想求dp[i][j],假设你知道了子问题dp[i+1][j-1]的结果(s[i+1..j-1]中最长回文子序列的长度),你是否能想办法算出dp[i][j]的值(s[i..j]中,最长回文子序列的长度)呢?
这取决于s[i]和s[j]的字符:
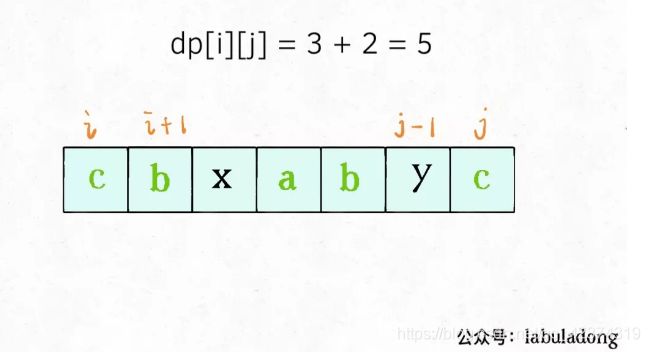
如果它俩相等,那么它俩加上s[i+1..j-1]中的最长回文子序列就是s[i..j]的最长回文子序列:
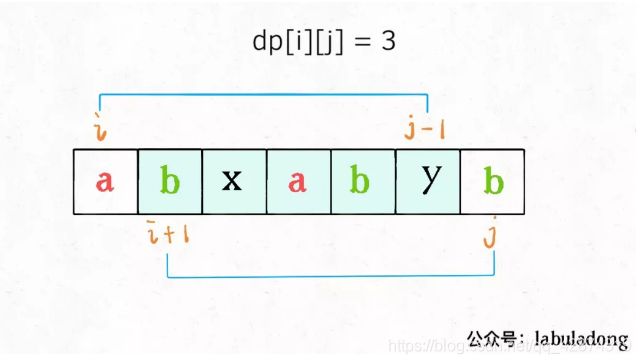
如果它俩不相等,说明它俩不可能同时出现在s[i..j]的最长回文子序列中,那么把它俩分别加入s[i+1..j-1]中,看看哪个子串产生的回文子序列更长即可:
以上两种情况写成代码就是这样:
if (s[i] == s[j])
// 它俩一定在最长回文子序列中
dp[i][j] = dp[i + 1][j - 1] + 2;
else
// s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长?
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
首先明确一下 base case,如果只有一个字符,显然最长回文子序列长度是 1,也就是dp[i][j] = 1,(i == j)。
因为i肯定小于等于j,所以对于那些i > j的位置,根本不存在什么子序列,应该初始化为 0。
另外,看看刚才写的状态转移方程,想求dp[i][j]需要知道dp[i+1][j-1],dp[i+1][j],dp[i][j-1]这三个位置;再看看我们确定的 base case,填入 dp 数组之后是这样:
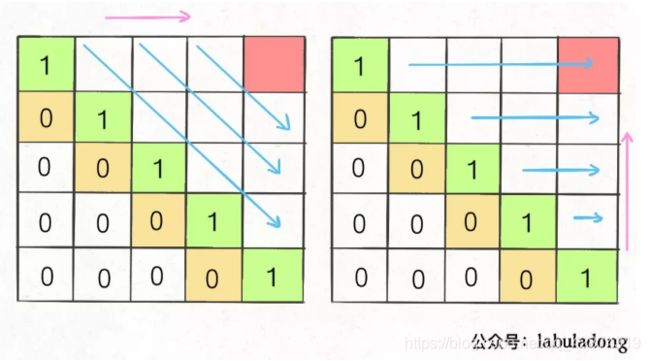
为了保证每次计算dp[i][j],左、下、左下三个方向的位置已经被计算出来,只能斜着遍历或者反着遍历:
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for(int i = 0; i < n; i++){
dp[i][i] = 1;
}
for(int i = n - 1; i >= 0; i--){
for(int j = i + 1; j < n; j++){
// 状态转移方程
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j - 1] + 2;
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][n - 1]; //整个 s 的最长回文子串长度
}
}
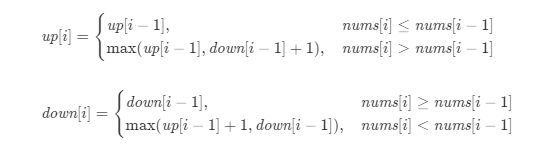
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lBO99t4Y-1619148283422)(C:\Users\lp\AppData\Roaming\Typora\typora-user-images\image-20210421112228485.png)]](http://img.e-com-net.com/image/info8/250920fa4a2243d98a66567bcc38a0e5.jpg)