【YOLO v4】常见的非极大值抑制方法：(Hard) NMS、Soft NMS、DIoU NMS

NMS（Non maximum suppression）是在object detection算法中必备的后处理步骤，目的是用来去除重复框，也就是降低误检（false positives）。NMS是一种速度慢的算法，其时间复杂度为O（N ^ 2），所以NMS代码的质量直接关系到推理结果的准确性和速度，需要不断调试NMS方法。

一、(Hard) NMS

Hard NMS 就是我们最经常说的NMS，也是最原始的NMS，后面扩展的NMS都是在Hard NMS基础上修改的。

1.1、IoU

IoU(Intersection over Union)，也就是我们常说的交并比。简单来说IOU就是用来度量目标检测中预测框与真实框的重叠程度。

IoU公式：

$IoU=\frac{|A\bigcap B|}{|A\bigcup B|}$
显而易见，IOU的值越高也说明A框与B框重合程度越高，代表模型预测越准确。反之，IOU越低模型性能越差。

1.2、Hard NMS算法流程

1. 先对网络预测出的所有边界框按分数（属于某个种类的概率）由高到低排列；
2. 再取分数最高的预测框作为target，分别算出target与其余预测框的IoU；
3. 若IoU大于某一设定的IoU阈值，则认为该预测框与target同时负责预测同一个物体，所以将该预测框删除，否则就保留该预测框；
4. 接着在未被删除的预测框中选择分数最高的预测框作为新的target，重复上面的步骤，直到判断出所有框是否应该删除。

1.3、实例分析

对于每一个种类的概率，比如Dog，我们将所有98个框按照预测概率从高到低排序（为方便计算，排序前可以剔除极小概率的框，也就是把它们的概率置为0），然后通过非极大抑制NMS方法，继续剔除多余的框，步骤如下：

1. 首先我们会根据一个IoU阈值剔除极小概率的框，也就是把它们的概率置为0；
2. 再将所有的狗的预测框按分数从大到小排序，如下图；
   
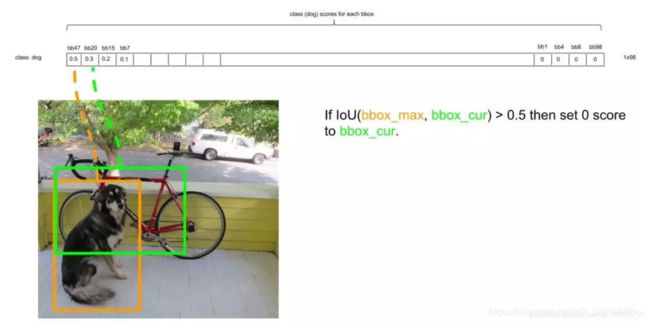
3. 下一步，设最大的框为target，依次比较它和其他非0框的IoU，如果大于设定的IoU（这里是0.5），就将其置为0，如下target和第二个框的IoU明显大于阈值0.5，所以舍去第二个框，设为0，如下图；
   
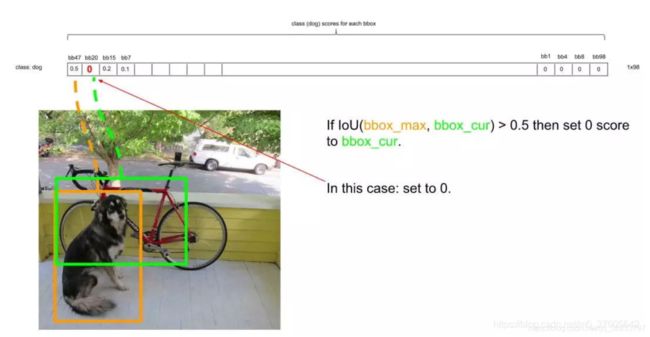
4. 继续扫描到第三个框，它与最大概率框的IOU小于0.5，需要保留，如下图：
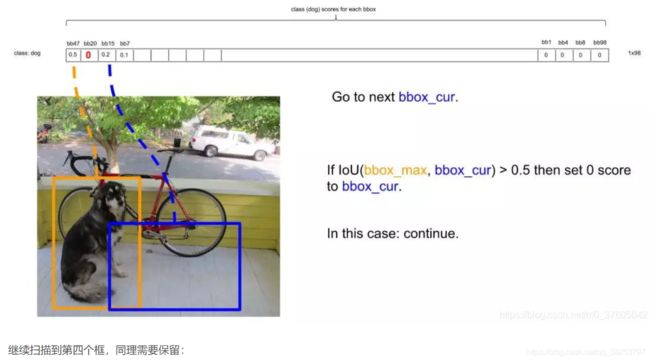
5. 继续扫描到第四个框，同理需要保留，如下图：
   
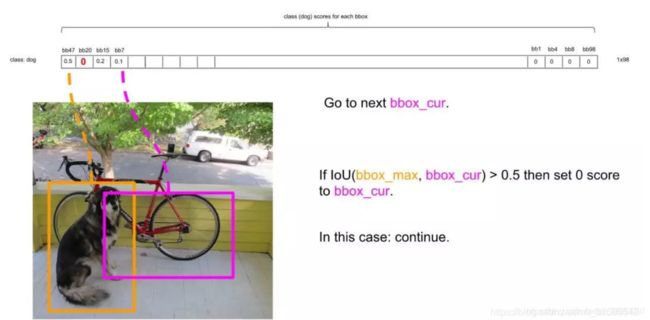
6. 继续扫描后面的框，直到所有框都与第一个框比较完毕。此时保留了不少框。
7. 接下来，以次大概率的框（因为一开始排序过，它在顺序上也一定是保留框中最靠近上一轮的基础框的）为基础，将它后面的其它框于之比较，如下图：
   
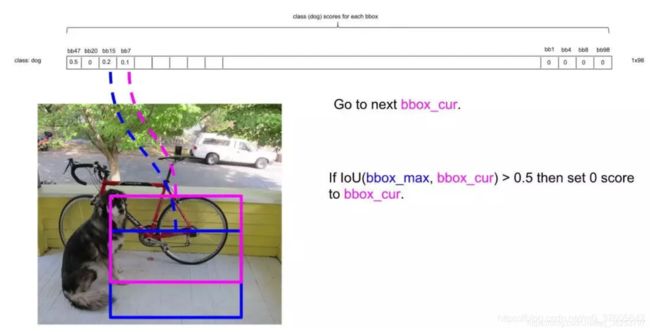
   IOU大于0.5，所以可以剔除第4个框：
   
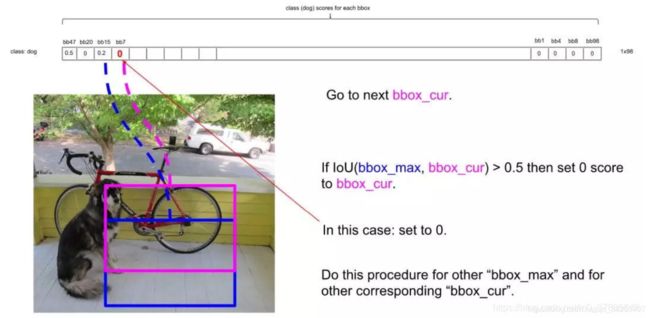
8. 假设在经历了所有的扫描之后，对Dog类别只留下了两个框，如下：
   
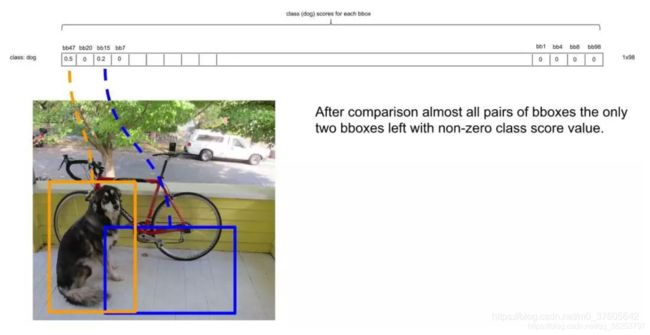
   已经无法再删除剩下的框了，这时候，或许会有疑问：明显留下来的蓝色框，并非Dog，为什么要留下？因为对计算机来说，图片可能出现两只Dog，保留概率不为0的框是安全的。不过的确后续设置了一定的阈值（比如0.3）来删除掉概率太低的框，这里的蓝色框在最后并没有保留，因为它在最后会因为阈值不够而被剔除。
9. 上面描述了对Dog种类进行的框选择。接下来，我们还要对其它19种类别分别进行上面的操作。
10. 最后进行纵向跨类的比较（为什么？因为上面就算保留了橘色框为最大概率的Dog框，但该框可能在Cat的类别也为概率最大且比Dog的概率更大，那么我们最终要判断该框为Cat而不是Dog）。判定流程和法则如下：
    
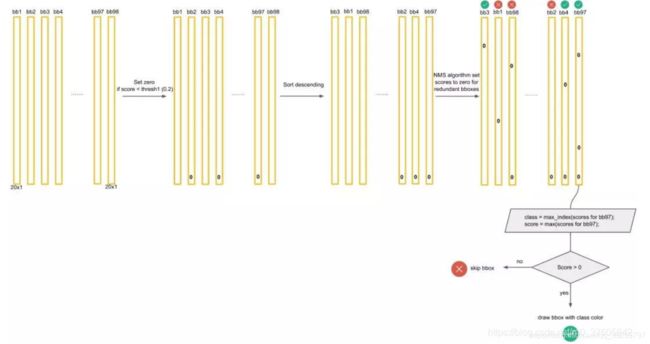
    得到最后的结果：
    

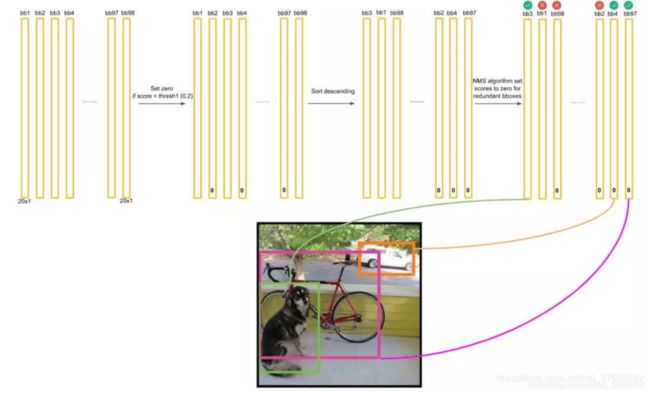
二、Soft NMS

论文链接: https://arxiv.org/pdf/1704.04503.pdf.

2.1、背景

绝大部分目标检测方法，最后都要用到 NMS-非极大值抑制进行后处理。

通常的做法是将检测框按得分排序，然后保留得分最高的框，同时删除与该框重叠面积大于一定比例的其它框。具体的内容看上面这里不赘述。

这种贪心式方法存在如下图所示的问题： 红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。

另一方面，NMS的阈值也不太容易确定，设小了会出现下图的情况（绿色框因为和红色框重叠面积较大而被删掉），设置过高又容易增大误检。

针对NMS存在的问题，我们提出了一种新的Soft-NMS算法。它只需改动一行代码即可有效改进传统贪心NMS算法。

2.2、Soft NMS算法

算法思路：不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。
用原文的话讲：An algorithm which decays the detection scores of all other objects as a continuous function of their overlap with M
我们基于重叠部分的大小为相邻检测框设置一个衰减函数而非彻底将其分数置为零。简单来讲，如果一个检测框与M有大部分重叠，它会有很低的分数；而如果检测框与M只有小部分重叠，那么它的原有检测分数不会受太大影响。
总体来说，Soft NMS算法的流程和NMS的差不多，就是在计算出target和其他框的IOU后，如果这个IOU大于设定的阈值时，我们不是一刀切的将预测框的score置0，而是用一个函数来衰减预测框score
而这个衰减函数的设计一般有两种:
1. 线性加权
$$S_i==\{\begin{array}{ll}{S}_i,& \text{iou(M,bi)≤Nt}\\ S_i(1-iou(M,b_i)),& \text{iou(M,bi)≥Nt}\end{array}$$但是这个公式是不连续的，这样会导致box集合中的score出现断层，因此就有了下面这个Soft NMS式子
2. 高斯加权（大部分实验中采用的式子）
$$S_i=S_i{e}^{-\frac{iou(M,b_i)}{\sigma }},任意b_i\notin D$$

NMS 与 Soft NMS 流程对比图:

2.3、实例

1、 比如一张人脸上有3个重叠的bounding box, 置信度分别为0.9, 0.7, 0.85 。
2、选择得分最高的建议框，经过第一次处理过后，得分变成了0.9, 065, 0.55。
3、这时候再选择第二个bounding box作为得分最高的，处理后置信度分别为0.65, 0.45
4、最后选择第三个，处理后得分不改变。
5、最终经过soft-nms抑制后的三个框的置信度分别为0.9, 0.65, 0.45。
6、最后设置阈值，将得分si小于阈值（假设是0.5）的去掉0.45。

假如还检测出了3号框，而我们的最终目标是检测出1号和2号框，并且剔除3号框，原始的nms只会检测出一个1号框并剔除2号框和3号框，而softnms算法可以对1、2、3号检测狂进行置信度排序，可以知道这三个框的置信度从大到小的顺序依次为：1->2->3（由于是使用了惩罚，IoU越大，得分越低，所有可以获得这种大小关系），如果我们再选择了合适的置信度阈值，就可以保留1号和2号，同时剔除3号，实现我们的功能。

2.4、总结优缺点

优点：

1. 它仅需要对传统的NMS算法进行简单的改动（一行代码）且不增额外的参数，具有与传统NMS相同的算法复杂度，使用高效
2. 不需要额外的训练，并易于实现，它可以轻松的被集成到任何物体检测流程中。

缺点：

1. 依然使用手工设置的值，依然存在很大的局限性，所以该算法依然存在改进的空间。
2. 效果方面不好说，具体的项目还是要具体的调试。（看到网络好多人说用了反而效果变差了）

三、DIoU NMS

论文: https://arxiv.org/pdf/1911.08287.pdf.

3.1、背景

在经典的NMS中，得分最高的检测框和其它检测框逐一算出一个对应的IOU值，并将该值超过NMS threshold的框全部过滤掉。可以看出，在经典NMS算法中，IOU是唯一考量的因素。但是在实际应用场景中，当两个不同物体挨得很近时，由于IOU值比较大，往往经过NMS处理后，只剩下一个检测框，这样导致漏检的错误情况发生。

一个成熟的IoU衡量指标应该要考虑预测框与真实框的重叠面积、中心点距离、长宽比三个方面。但是IoU 只考虑到了预测框与真实框重叠区域，并没有考虑到中心点距离、长宽比。

基于此，DIOU-NMS就不仅仅考虑IOU，还考虑两个框中心点之间的距离。如果两个框之间IOU比较大，但是两个框的中心距离比较大时，可能会认为这是两个物体的框而不会被过滤掉。

具体的IoU、GIoU、DIoU、CIoU的细节可以看我的另一篇博客: Bounding Box regression loss: IoU Loss、GIoU Loss、DIoU Loss、CIoU Loss.

3.2、DIoU

DIoU (Distance-IoU )。简单地在IoU loss基础上添加一个惩罚项，该惩罚项用于最小化两个bbox的中心点距离。

DIoU公式：

$$DIoU=IoU-\frac{{\rho }^2(b,b^{gt})}{c^2}=IoU-\frac{d^2}{c^2}$$ $-1\le DIoU\le 1$

如下图，绿色框代表真实框，黑色框代表预测框，$b$为预测框的中心，$b^{gt}$为真实框的中心，${\rho }^2(b,b^{gt})$代表真实框与预测框中心距离的平方$d^2$,$c$表示两个框的最小闭包区域（同时包含了预测框和真实框的最小矩形框）的对角线长度。

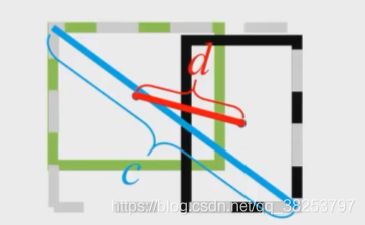
Hard NMS 和 DIoU NMS比较：就是target和其他检测框的计算IoU的方式变成了DIoU，其他所有操作都和hard nms 完全相同

四、代码实现

以下代码主要实现了：hard_nms、soft_nms、diou_nms以及一些hard nms的改进版本。

import torch
import numpy as np
import torchvision
import math

def non_max_suppression(prediction, conf_thres=0.1, nms_thres=0.6, multi_cls=True, method='diou_nms'):
    """
        Removes detections with lower object confidence score than 'conf_thres'
        Non-Maximum Suppression to further filter detections.
        param:
             prediction: [batch, num_anchors, (x+y+w+h+1+num_classes)]  3个anchor的预测结果总和
             conf_thres: 先进行一轮筛选，将分数过低的预测框（iou_thres, 就将那个预测框置0
             multi_label: 是否是多标签
             method: nms方法  (https://github.com/ultralytics/yolov3/issues/679)
                              (https://github.com/ultralytics/yolov3/pull/795)
                        -hard_nms: 普通的 (hard) nms 官方实现(c函数库),可支持gpu,只支持单类别输入
                        -hard_nms_batch: 普通的 (hard) nms 官方实现(c函数库),可支持gpu,支持多类别输入
                        -hard_nms_myself: 普通的 (hard) nms 自己实现的,只支持单类别输入
                        -and: 在hard-nms的逻辑基础上，增加是否为单独框的限制，删除没有重叠框的框（减少误检）。
                        -merge: 在hard-nms的基础上，增加保留框位置平滑策略（重叠框位置信息求解平均值），使框的位置更加精确。
                        -soft_nms: soft nms 用一个衰减函数作用在score上来代替原来的置0
                        -diou_nms: 普通的 (hard) nms 的基础上引入DIoU(普通的nms用的是iou)
        Returns detections with shape:
            (x1, y1, x2, y2, object_conf, conf, class)
    """
    # Box constraints
    min_wh, max_wh = 2, 4096  # (pixels) 宽度和高度的大小范围 [min_wh, max_wh]
    output = [None] * len(prediction)  # batch_size个output  存放最终筛选后的预测框结果
    for image_i, pred in enumerate(prediction):
        # 开始  pred = [12096, 25]
        # 第一层过滤   根据conf_thres虑除背景目标(conf
        pred = pred[pred[:, 4] > conf_thres]  # pred = [45, 25]

        # 第二层过滤   虑除超小anchor标和超大anchor  x=[45, 25]
        pred = pred[(pred[:, 2:4] > min_wh).all(1) & (pred[:, 2:4] < max_wh).all(1)]

        # 经过前两层过滤后如果该feature map没有目标框了，就结束这轮直接进行下一个feature map
        if len(pred) == 0:
            continue

        # 计算 score
        pred[..., 5:] *= pred[..., 4:5]  # score = obj_conf * cls_conf

        # Box (center x, center y, width, height) to (x1, y1, x2, y2)
        box = xywh2xyxy(pred[:, :4])

        # Detections matrix nx6 (xyxy, conf, cls)
        if multi_cls or conf_thres < 0.01:
            # 第三轮过滤: 针对每个类别score(obj_conf * cls_conf) > conf_thres
            # 这里一个框是有可能有多个物体的，所以要筛选
            # nonzero: 获得矩阵中的非0数据的下标  t(): 将矩阵拆开
            # i: 下标   j: 类别   shape=43  过滤了两个score太低的
            i, j = (pred[:, 5:] > conf_thres).nonzero(as_tuple=False).t()
            # pred = [43, xyxy+conf+class]
            pred = torch.cat((box[i], pred[i, j + 5].unsqueeze(1), j.float().unsqueeze(1)), 1)
        else:  # best class only
            conf, j = pred[:, 5:].max(1)  # 一个类别直接取分数最大类的即可
            pred = torch.cat((box, conf.unsqueeze(1), j.float().unsqueeze(1)), 1)[conf > conf_thres]

        # 第三轮过滤后如果该feature map没有目标框了，就结束这轮直接进行下一个feature map
        if len(pred) == 0:
            continue
        # 第四轮过滤  这轮可有可无，一般没什么用
        # pred = pred[torch.isfinite(pred).all(1)]

        # 降序排列 为NMS做准备
        pred = pred[pred[:, 4].argsort(descending=True)]

        # Batched NMS
        # Batched NMS推理时间：0.054
        if method == 'hard_nms_batch': # 普通的(hard)nms: 官方实现(c函数库),可支持gpu,但支持多类别输入
            # batched_nms：参数1 [43, xyxy]  参数2 [43, score]  参数3 [43, class]  参数4 [43, nms_thres]
            output[image_i] = pred[torchvision.ops.boxes.batched_nms(pred[:, :4], pred[:, 4], pred[:, 5], nms_thres)]
            # print("hard_nms_batch")
            continue

        # All other NMS methods
        det_max = []  # 存放分数最高的框 即target
        cls = pred[:, -1]
        for c in cls.unique():  # 对所有的种类(不重复)
            dc = pred[cls == c]  # dc: 选出pred中所有类别是c的结果
            n = len(dc)
            if n == 1:
                det_max.append(dc)  # No NMS required if only 1 prediction
                continue
            elif n > 500:# 密集性 主要考虑到NMS是一个速度慢的算法（O(n^2)）,预测框太多,算法的效率太慢 所以这里筛选一下（最多500个预测框）
                dc = dc[:500]  # limit to first 500 boxes: https://github.com/ultralytics/yolov3/issues/117

            # 推理时间：0.001
            if method == 'hard_nms':  # 普通的(hard)nms: 只支持单类别输入
                det_max.append(dc[torchvision.ops.boxes.nms(dc[:, :4], dc[:, 4], nms_thres)])

            # 推理时间：0.00299 是官方写的3倍
            elif method == 'hard_nms_myself':  # Hard NMS 自己写的 只支持单类别输入
                while dc.shape[0]:  # dc.shape[0]: 当前class的预测框数量
                    det_max.append(dc[:1])  # 让score最大的一个预测框(排序后的第一个)为target
                    if len(dc) == 1:  # 出口 dc中只剩下一个框时，break
                        break
                    # dc[0] ：target     dc[1:] ：其他预测框
                    diou = bbox_iou(dc[0], dc[1:])  # 计算 diou
                    dc = dc[1:][diou < nms_thres]  # remove dious > threshold

            # 在hard-nms的逻辑基础上，增加是否为单独框的限制，删除没有重叠框的框（减少误检）。
            elif method == 'and':  # requires overlap, single boxes erased
                while len(dc) > 1:
                    iou = bbox_iou(dc[0], dc[1:])  # iou with other boxes
                    if iou.max() > 0.5:  # 删除没有重叠框的框/iou小于0.5的框（减少误检）
                        det_max.append(dc[:1])
                    dc = dc[1:][iou < nms_thres]  # remove ious > threshold

            # 在hard-nms的基础上，增加保留框位置平滑策略（重叠框位置信息求解平均值），使框的位置更加精确。
            elif method == 'merge':  # weighted mixture box
                while len(dc):
                    if len(dc) == 1:
                        det_max.append(dc)
                        break
                    i = bbox_iou(dc[0], dc) > nms_thres  # i = True/False的集合
                    weights = dc[i, 4:5]     # 根据i，保留所有True
                    dc[0, :4] = (weights * dc[i, :4]).sum(0) / weights.sum()  # 重叠框位置信息求解平均值
                    det_max.append(dc[:1])
                    dc = dc[i == 0]

            # 推理时间：0.0030s
            elif method == 'soft_nms':  # soft-NMS      https://arxiv.org/abs/1704.04503
                sigma = 0.5  # soft-nms sigma parameter
                while len(dc):
                    # if len(dc) == 1:  这是U版的源码 我做了个小改动
                    #     det_max.append(dc)
                    #     break
                    # det_max.append(dc[:1])
                    det_max.append(dc[:1])   # 保存dc的第一行  target
                    if len(dc) == 1:
                        break
                    iou = bbox_iou(dc[0], dc[1:])  # 计算target与其他框的iou

                    # 这里和上面的直接置0不同，置0不需要管维度
                    dc = dc[1:]  # dc=target往后的所有预测框
                    # dc必须不包括target及其前的预测框，因为还要和值相乘, 维度上必须相同
                    dc[:, 4] *= torch.exp(-iou ** 2 / sigma)  # 得分衰减
                    dc = dc[dc[:, 4] > conf_thres]

            # 推理时间：0.00299
            elif method == 'diou_nms':  # DIoU NMS  https://arxiv.org/pdf/1911.08287.pdf
                while dc.shape[0]:  # dc.shape[0]: 当前class的预测框数量
                    det_max.append(dc[:1])  # 让score最大的一个预测框(排序后的第一个)为target
                    if len(dc) == 1:  # 出口 dc中只剩下一个框时，break
                        break
                    # dc[0] ：target     dc[1:] ：其他预测框
                    diou = bbox_iou(dc[0], dc[1:], DIoU=True)  # 计算 diou
                    dc = dc[1:][diou < nms_thres]  # remove dious > threshold  保留True 删去False

        if len(det_max):
            det_max = torch.cat(det_max)  # concatenate  因为之前是append进det_max的
            output[image_i] = det_max[(-det_max[:, 4]).argsort()]  # 排序

    return output

def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False):
    """iou giou diou ciou
    Args:
        box1: 预测框
        box2: 真实框
        x1y1x2y2: False
    Returns:
        box1和box2的IoU/GIoU/DIoU/CIoU
    """
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.t()  # 转置 ？？？

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2  # b1左上角和右下角的x坐标
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2  # b1左下角和右下角的y坐标
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2  # b2左上角和右下角的x坐标
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2  # b2左下角和右下角的y坐标

    # Intersection area  tensor.clamp(0): 将矩阵中小于0的元数变成0
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1
    union = (w1 * h1 + 1e-16) + w2 * h2 - inter  # 1e-16: 防止分母为0

    iou = inter / union  # iou
    if GIoU or DIoU or CIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
        if GIoU:  # Generalized IoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = cw * ch + 1e-16  # convex area
            return iou - (c_area - union) / c_area  # return GIoU
        if DIoU or CIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            # convex diagonal squared
            c2 = cw ** 2 + ch ** 2 + 1e-16
            # centerpoint distance squared
            rho2 = ((b2_x1 + b2_x2) - (b1_x1 + b1_x2)) ** 2 / 4 + ((b2_y1 + b2_y2) - (b1_y1 + b1_y2)) ** 2 / 4
            if DIoU:
                return iou - rho2 / c2  # DIoU
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / (1 - iou + v)
                return iou - (rho2 / c2 + v * alpha)  # CIoU
    return iou

def xywh2xyxy(x):
    # Convert nx4 boxes from [x, y, w, h] to [x1, y1, x2, y2] where xy1=top-left, xy2=bottom-right
    y = torch.zeros_like(x) if isinstance(x, torch.Tensor) else np.zeros_like(x)
    y[:, 0] = x[:, 0] - x[:, 2] / 2  # top left x
    y[:, 1] = x[:, 1] - x[:, 3] / 2  # top left y
    y[:, 2] = x[:, 0] + x[:, 2] / 2  # bottom right x
    y[:, 3] = x[:, 1] + x[:, 3] / 2  # bottom right y
    
    return y

总结：

1. hard_nms：直接删除相邻的同类别目标，密集目标的输出不友好。
2. hard_nms_batch：普通的 (hard) nms 官方实现(c函数库),可支持gpu,支持多类别输入
3. hard_nms_myself：普通的 (hard) nms 自己实现的,只支持单类别输入
4. and：在hard-nms的逻辑基础上，增加是否为单独框的限制，删除没有重叠框的框（减少误检）。
5. merge：在hard-nms的基础上，增加保留框位置平滑策略（重叠框位置信息求解平均值），使框的位置更加精确。
6. soft_nms：改变其相邻同类别目标置信度（有关iou的函数），后期通过置信度阈值进行过滤，适用于目标密集的场景。
7. diou_nms：在hard-nms的基础上，用diou替换iou，里有参照diou的优势。

作者实验1：

https://github.com/ultralytics/yolov3/issues/679
python3 test.py --weights ultralytics68.pt --nms-thres 0.6 --img-size 512 --device 0

NMS方法	Speed mm:ss	COCO mAP @0.5…0.95	COCO mAP @0.5
hard_nms	05：08	39.7	60.3
hard_nms_batch	06：00	39.7	60.3
hard_nms_myself	08：20	39.7	60.3
and	07：38	39.6	60.1
merge	11：25	40.2	60.4
soft_nms	12：00	39.1	58.7

作者实验2：

https://github.com/ultralytics/yolov3/pull/795
python3 test.py --weights ultralytics68.pt --iou-thres 0.6 --img 608

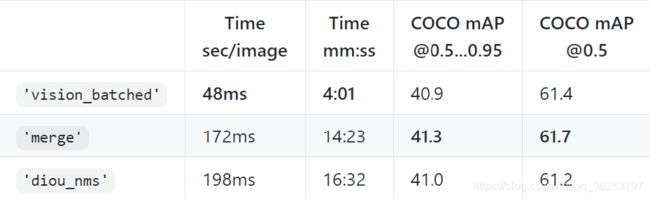
NMS方法	Speed mm:ss	COCO mAP @0.5…0.95	COCO mAP @0.5
hard_nms_batch	04：01	40.9	61.4
merge	14：23	41.3	61.7
diou_nms	16：32	41.0	61.2

从实验的结果来看，merge是最好的，但不同的数据集可能结果不一定一样。以后实验可以多关注merge nms、diou nms、soft nms这三种方法。

其他的NMS

YOLOv3的作者还对其他的NMS（如Fast NMS, Matrix NMS、Cluster NMS等）做了实验，后期可能会继续更新这部分内容，感兴趣也可以自己学习作者源码： 源码 issue 679.

Reference

soft nms 论文翻译.
soft nms.
代码.
代码.

其他的nms 1.
其他的nms 2.
Fast NMS.
Matrix NMS.