python信号处理加汉明窗_Python学习-Scipy库信号处理signal(过滤、快速傅里叶变换、信号窗函数、卷积)...

Python学习-Scipy库信号处理signal

目录

1、过滤：以某种方式修改输入信号

2、快速傅里叶变换

3、信号窗函数

4、卷积

导入库

import matplotlib.pyplot as plt

import scipy.signal as sgn

import numpy as np

1、过滤：以某种方式修改输入信号

1)快速线性两次应用滤波函数 filtfilt()

参数介绍：

b: 集合，滤波器所提供的分子系数向量

a: 集合，滤波器所提供的分母系数向量

x: 数组，要过滤信号的数据数组

axis: 指定要过滤x数据数组的轴，默认axis=-1不指定

padtype: 决定用于应用滤波器的填充信号扩展类型，‘odd’(奇数) ‘even’(偶数) ‘constant’(常量数值) ‘None’(不使用填充)

padlen: 在应用滤波器之前，在轴两端扩展x的元素数量，小于x.shape-1，默认3*max(len(a), len(b))

method: 确定处理信号边缘的方法，'pad’由padtype和padlen决定，'gust’使用Gustafssion的方法

irlen: 整型或None，当method为’gust’时，指定滤波器的脉冲响应的长度，对于长信号可以提高滤波器的性能

2)巴特沃斯数字和模拟滤波器设计函数：设置N阶数字或模拟Butterworth滤波器并返回滤波器系数 butter()

参数介绍：

N: 整型，指定过滤器的阶数

Wn: 集合，指定截止频率或长度为2的列表

btype: 过滤器类型，'lowpass’低通 'highpass’高通 'bandpass’带通 'bandstop’带阻

analog: False数字滤波器，True模拟滤波器

output: 输出类型，'ba’返回数组b、a，'zpk’返回数组z、p、浮点型k，'sos’返回数组sos

plt.rc('font', family='simhei', size=15) # 设置中文显示，字体大小

plt.rc('axes', unicode_minus=False) # 该参数解决负号显示的问题

# np.random.seed(29929) # 设置random生成随机数时，每次都相同

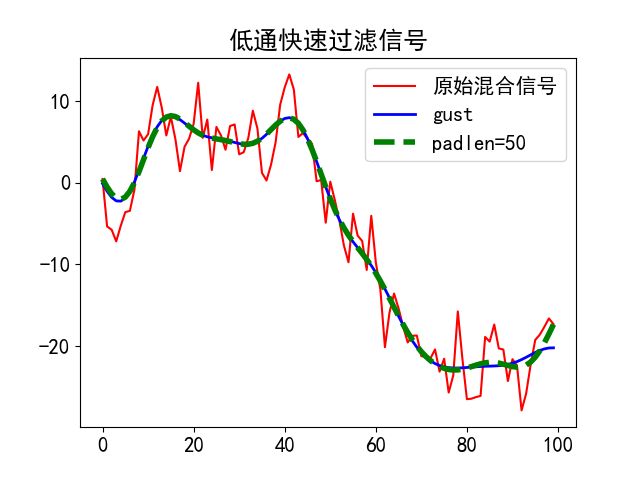
# 创建一个低通巴特沃斯滤波器，8阶过滤器，截止频率为125Hz

b, a = sgn.butter(N=8, Wn=0.125, btype='lowpass', analog=False, output='ba')

n = 100 # 样本数100个

sig = np.random.randn(n)**2 + 3*np.random.randn(n).cumsum() # 建立一个由两个随机标准正态分布叠加的混合信号

f_gust = sgn.filtfilt(b=b, a=a, x=sig, method='gust') # 基于Gustafsson方法信号快速两次应用过滤

f_pad = sgn.filtfilt(b=b, a=a, x=sig, padlen=50) # 信号快速两次应用过滤，padlen样本信号x两端扩展45个元素

plt.figure(num=1)

plt.plot(sig, 'r-', label='原始混合信号')

plt.plot(f_gust, 'b-', lw=2, label='gust')

plt.plot(f_pad, 'g--', lw=4, label='padlen=50')

plt.legend(loc='best')

plt.title('低通快速过滤信号')

plt.show()

输出

2、快速傅里叶变换：利用计算机进行离散傅里叶变换

import scipy.fftpack as fpk

1)快速计算离散傅里叶变换 fft()

参数介绍;

x: 需要处理的数据集合

n: 傅里叶变换长度，nx.shape,补充0

axis: 指定fft的轴方向，默认-1，最后一个轴

overwrite: True销毁x,，False不销毁

返回值：

y(0),y(1),…,y(n-1)，其中y(j)=(xexp(-2pi*sqrt(-1)jnp.arange(N)/N)).sum()

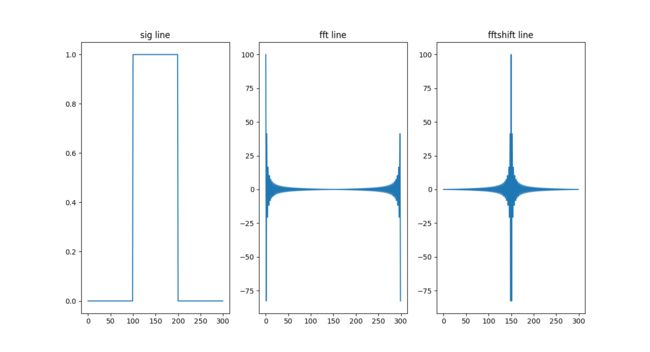
sig = np.repeat([0.0, 1.0, 0.0], 100)

A = fpk.fft(x=sig)

plt.figure(num=2, figsize=(10, 10))

plt.subplot(131)

plt.plot(sig) # 绘制原始信号

plt.title('sig line')

plt.subplot(132)

plt.plot(A) # 绘制傅里叶变换后的信号图像

plt.title('fft line')

2)调整频谱显示范围[0, N]到[-N/2, N/2-1] (N为奇数)或[-(N-1)/2, (N-1)/2] (N为偶数) fftshift()

参数介绍：

x: 需要调整的集合

axis: 调整维度方向

B = fpk.fftshift(A)

plt.subplot(133)

plt.plot(B) # 范围调整后的傅里叶变换信号图像

plt.title('fftshift line')

plt.show()

输出

3、信号窗函数

通过傅里叶变换得到的分析频谱，会因采样不合适，存在频谱泄露现象(不同频率的信号能量互相叠加)

需要对信号加窗，修正频谱泄露问题 矩形窗、三角窗、汉宁窗、高斯窗

汉宁信号窗函数 hann()

参数说明：

M: 输出窗的点数，<=0: 返回空数组

sym: True，对称窗，用于过滤器设计；False,周期窗，用于光谱分析

返回值：数据型窗值，最大标准化为1

plt.rc('font', family='simhei', size=15) # 设置中文显示，字体大小

plt.rc('axes', unicode_minus=False) # 该参数解决负号显示的问题

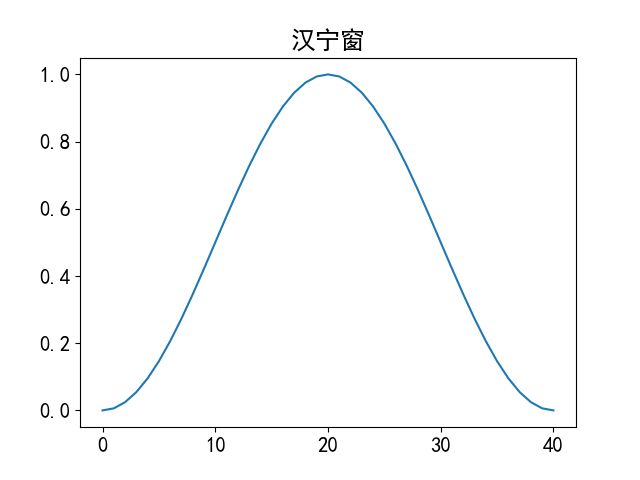
plt.figure(num=3)

han = sgn.hann(41)

plt.plot(han)

plt.title('汉宁窗')

输出

4、卷积

基于两个多维度数组的卷积 convolove()

参数说明：

in1: 第一个输入函数，主要指需要处理的信号源数据

in2: 第二个输入函数，提供另外一个处理第一个信号的数据源，必须与in1保持一样的维度

mode: 用于指定该函数输出方式，'full’完全离散线性卷积，'valid’输出仅包含那些不依赖于零填充的元素，

'same’输出与in1的大小相同，以‘full’输出为中心

method: 卷积方法，'auto’自动选择直接或傅里叶方法，'direct’调用’fftconvolve’函数利用傅里叶变换方法，

'fft’指定卷积核方法

返回值：N维数组，包含in1和in2的离散线性卷积的子集

plt.rc('font', family='simhei', size=15) # 设置中文显示，字体大小

plt.rc('axes', unicode_minus=False) # 该参数解决负号显示的问题

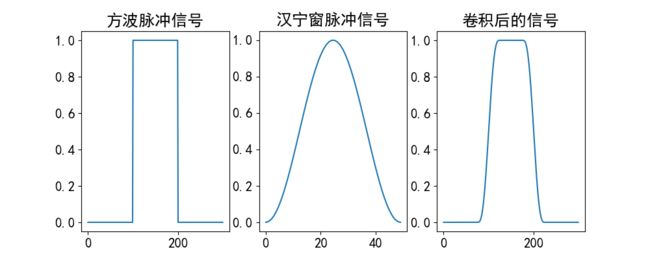
fig = plt.figure(num=4, figsize=(10, 4))

plt.subplot(131)

sig = np.repeat([0.0, 1.0, 0.0], 100)

plt.plot(sig)

plt.title('方波脉冲信号')

han = sgn.hanning(50)

plt.subplot(132)

plt.plot(han)

plt.title('汉宁窗脉冲信号')

f = sgn.convolve(in1=sig, in2=han, mode='same')/sum(han)

plt.subplot(133)

plt.plot(f)

plt.title('卷积后的信号')

plt.show()

输出

标签：滤波器,plt,Python,signal,卷积,Scipy,sig,信号,傅里叶

来源： https://blog.csdn.net/weixin_41387192/article/details/111158534