【点宽专栏】国信证券——关于量化选股之聚类分析的探讨

前言

本文基于《国信技术面量化选股系列：价格路径对收益的影响》（国信证券：20160909）和《基于k-means聚类的多因子特征检验》（国信证券：20161205）两份研报（研报见评论一附件）的思路进行实证和探讨。上述两份研报在下文中分别简称为《价格》和《聚类》。

研报内容简述

1.《价格》一文探讨了已实现波动率、偏度和峰度对收益的影响并主要得到了以下结论：

在上述三个指标的计算中，基于5分钟数据计算的三指标为有效选股因子，但用日数据则失效。
上述三因子在周度和月度范围内都是有效指标，即对时间周期不敏感。
上述三因子在沪深300和中证500股票池中都是有效的，即对选股池风格不敏感。
三因子中偏度因子的单调性表现最好，无论是周度还是月度，随着偏度增加，下期收益显著降低。
与偏度相比，峰度和波动率则呈现出某种非单调特征。但大体上讲，高峰度时或高波动率时，下期收益的下降都比较明显。
上述结论是在基于截面数据计算的三因子指标的条件下得到的，可以作为选股指标，但在基于同一标的资产的时间序列数据的条件下尚未发现明显的规律，关于上述因子的择时策略有待进一步研究。
2.《聚类》一文以市值和波动率为特征指标使用k-means聚类方法将全A股分为5簇并分析不同簇集里的各项指标的差异。总的来说有以下结论：

尽管划分的依据是市值和波动率，但划分后的5个类别的盈利、增长、换手率等因子的数值特征也是显著不同的。波动率对于营收增长有显著的相关性，高波动率股票的整体营收增长率更高。而对于ROE因子，则体现出显著的市值特征，大市值股票的整体ROE更高，对于EP和换手率，市值和波动率特征同时显著。
以IC（Information coefficient）作为聚类检验的标准，在整体全A股的IC不显著因子中，不同聚类簇集的IC会体现出高于整体的显著水平。对于换手率、动量、波动率等价量因子，大市值的因子显著性是低于小市值组合的，其中以大市值、低波动率的组合最为显著。对于小市值组合中，高波动率组合的因子显著性较好，包括财务因子和价量因子都较为明显。对于财务因子而言，显著性更多的体现在大市值的两个组合之中。

本文主要完成工作

1.讨论股票的已实现波动率、偏度和峰度与未来收益率的关系。
2.以k-means聚类方法对波动率、偏度和峰度三个特征指标进行聚类并讨论聚类后的簇集特征。
3.基于SOM神经网络为方法的聚类分析。
4.以2、3部分中的聚类结果构建投资策略进行样本外回测并回测结果进行讨论。

一、股票的已实现波动率、偏度和峰度与未来收益率的关系

数据说明：本文使用的数据为沪深300成分股20120101-20151231期间的截面数据，数据频率10分钟（剔除数据不完全的股票以及正常股票的停牌期间）。

方法：以10分钟频率数据计算股票过去一周的已实现波动率、已实现偏度、已实现峰度（上述三指标以下依次简称为波动率、偏度和峰度）（指标的计算方法参见《价格》原文）并以该指标从小到大分为前20%、20%_40%、40%60%、60%_{80%和最后20%共计五组并依次记为“第一组”}“第五组”。比较每组下一周的收益率分布，并用t检验判断不同组别的收益率序列是否有显著性差别。

1.1 波动率-收益率

五组收益率的分布及每组的平均收益率如下图所示：

t检验的p值如下表所示：

注：（）表示在10%的水平下显著，（）表示5%水平下显著，（）为1%水平下显著，下同。

总结：
1）随着波动率的增加，收益率区间也有变大的趋势，同时收益率的分布显得更加分散。换而言之，波动率具有持续性，这与传统金融理论的“ARCH效应”（或称“群
聚效应”）相符。

2）从各组别的平均收益来看，不同组别的收益有所差别，但并没有出现单调性，而是体现出中间高两边低的特点，表明有着过高和过低波动率的股票未来的期望收益较低。

3）从t检验的p值来看，部分组别之间存在显著性的差别，表明基于波动率的高低进行的分类对未来收益是有显著影响的。

1.2 偏度-收益率

偏度-收益率的分布及检验如下图表所示：

总结：
1）随着偏度的增加，收益率的区间变窄，极端事件减少，但从峰值来看，收益率的分布却有分散的趋势。

2）从不同组别的平均收益来看，序列体现了较好的单调性，表明低偏度（左偏）的股票未来的期望收益较高，高偏度（右偏）反之。

3）遗憾的是从t检验的结果来看，不同组别的收益率序列在统计意义下并不存在显著的差别（尽管其均值不同）。

1.3 峰度-收益率

峰度-收益率的分布及检验如下图表所示：

总结：
1）随着峰度增加，收益率区间有变大的趋势，但峰值却先减后增，分布的集中度并无明显的规律。

2）不同组别的平均收益也无规律的变化。

3）从统计检验上看除个别组别外多数组别之间并未有显著差别。

1.4 本部分小节

本部分探讨了股票的已实现波动率、偏度和峰度对于其未来收益的影响。实证的部分结果与报告结论一致，例如波动率的持续性、偏度的单调性等。但也有部分结果存在较大的出入，例如高峰度与收益率的关系等。该结论的差异可能主要来自于使用了不同时间区间和不同数据频率的缘故。

二、k-means聚类的簇集特征

《聚类》一文以市值和波动率作为特征指标进行聚类，并以各项财务因子及其IC指标作为评价聚类效果的标准。由于目前AT中暂时无法直接获取各项基本面数据，同时也是承接前文的分析，本文的聚类指标为上述的三因子，评价指标为簇集收益率的特征。

2.1 三因子的分布规律

我们首先探讨一下三因子的分布规律，下面两张图分别给出了三因子的分布特征以及相互关系。

上图左上至右下依次为波动率分布、偏度分布、峰度分布和峰度的对数分布。从形态上看，偏度分布接近于正态分布，波动率和峰度则接近于对数正态分布，但从右下的图来看，峰度的对数分布倒更接近于卡方分布而非正态分布。

上图左上至右下的前三张图给出了三因子的两两关系，右下图为三因子的空间分布。左上图表明随着波动率的增加，偏度的绝对值在变小，即高波动率收益率的路径更接近于“不偏”的，而低波动率下的偏度可能会很大。右上图表明峰度会随着波动率的增加而变小，即收益率分布更为分散。左下图表明峰度与偏度之间存在对称性的V字形关系。

k-means聚类效果

关于k-means聚类方法的介绍参见《聚类》原文。在聚类之前我们需要对因子进行标准化处理，对于波动率和峰度因子，考虑到其对数正态特性，我们还对其进行了对数变换。下图给出了k=3~6的情况下的聚类效果和误差的收敛情况。

从上图来看，k-means算法能较好地根据样本点的空间位置将样本划分为不同的簇集。下图给出了以上四次聚类的过程中的误差收敛情况。

从上图来看，聚类误差随着迭代次数的增加而减少并最终收敛。但需要一提的是：①k-means算法的收敛一般是局部收敛，由于算法受初始值的影响很难实现全局收敛。②收敛值不一定是最小误差点，例如右下图就反映了这点。尽管算法本身存在一些不足，但总的来说，算法一般都能取得一个较好的局部最优解。

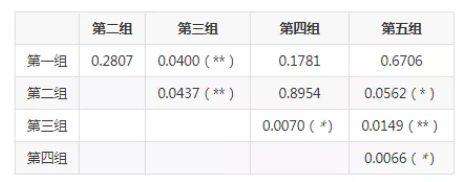
为了考察聚类效果，我们需要比较不同簇集下的收益率特征。以5中心聚类为例，我们统计不同簇集的平均收益率以及不同簇集之间的统计差异，如下面两张表格所示。

下表是不同组别t检验的p值。

尽管我们划分的依据是三因子，但显然不同组别之间的收益率序列也是存在显著性差异的。为了更直观地反映这点，我们给出第三组和第五组的收益率分布直方图。

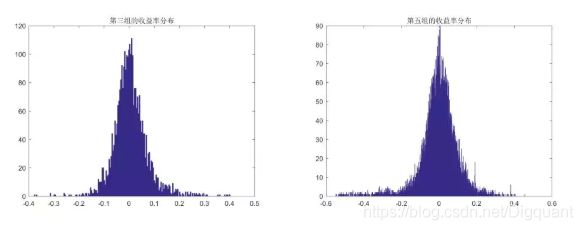
从上图中我们还是可以看出两组收益率的一些差别，例如第五组的收益率分布更加分散，且尾部更厚，尤其是损失的尾部。这表明该模式下未来收益的波动更大，且遭受极端损失的概率也更大。

在五中心聚类中，上述第三组的模式是我们最佳的投资机会，但该模式下平均0.0053的收益率并足以令人满意。因此我们接下来进行更为精细的聚类，以k=15为例，所得的各组平均收益率如下表。

假如以上表的结论进行投资，则拥有较高平均收益率的第三组、第十一组和第十三组是我们可能的投资机会。关于此的回测我们在第四部分给出。

本部分主要代码：

1.k-means聚类算法：
function [Centers,Clusters,err,idx]=kmeansclustering(Samples,k)
% k-means聚类
% 输出参数依次为：聚类中心、簇集集合、迭代误差、样本点类别
tic;
% 样本标准化-其中波动率和峰度进行了对数变换
Rvol=log(Samples(:,1));
Rskew=Samples(:,2);
Rkurt=log(Samples(:,3));
stvol=(Rvol-mean(Rvol))/std(Rvol);
stskew=(Rskew-mean(Rskew))/std(Rskew);
stkurt=(Rkurt-mean(Rkurt))/std(Rkurt);
stsamples=[stvol,stskew,stkurt];
n=length(stsamples);
cen_idx=ceil(rand(k,1)*n); % 初始中心点（编号）
Centers=stsamples(cen_idx,:);
[Clusters,err0]=classifying(Centers,stsamples); % 分类函数
err(1)=err0;
derr=1;
while derr~=0 % 迭代，直到收敛（即误差不再变化为止）
for i=1:k
Centers(i,:)=mean(Clusters{i});
end
[Clusters,err1,idx]=classifying(Centers,stsamples);
err=[err;err1]; %#ok 取消关于预先分配内存的警告
derr=err1-err0;
err0=err1;
end
toc;
%% 分类函数
function [Clusters,err,idx]=classifying(Centers,Samples)
% 在给定中心的情况下对样本进行归类
k=size(Centers,1);
Clusters=cell(1,k);
err=0;
n=length(Samples);
idx=zeros(n,1);
for i=1:n
subsample=Samples(i,:);
dist=sqrt(sum((ones(k,1)*subsample-Centers).^2,2));
[mind,minidx]=min(dist);
err=err+mind;
idx(i)=minidx;
end
for i=1:k
Clusters{i}=Samples(idx==i,:);
end

2.画聚类图和误差收敛图

function test3(Samples)
% 画聚类图和误差收敛图
figure;
%% k=3的聚类图
[~,Clusters,err1]=kmeansclustering(Samples,3);
subplot(2,2,1);
plot3(Clusters{1}(:,1),Clusters{1}(:,2),Clusters{1}(:,3),‘ro’);
hold on;plot3(Clusters{2}(:,1),Clusters{2}(:,2),Clusters{2}(:,3),‘b.’);
hold on;plot3(Clusters{3}(:,1),Clusters{3}(:,2),Clusters{3}(:,3),‘g+’);
grid on;hold off;
xlabel(‘波动率’);ylabel(‘偏度’);zlabel(‘峰度’);
set(gca,‘xlim’,[-5,5]);
title(‘三中心聚类图’);
%% k=4的聚类图
[~,Clusters,err2]=kmeansclustering(Samples,4);
subplot(2,2,2);
plot3(Clusters{1}(:,1),Clusters{1}(:,2),Clusters{1}(:,3),‘ro’);
hold on;plot3(Clusters{2}(:,1),Clusters{2}(:,2),Clusters{2}(:,3),‘b.’);
hold on;plot3(Clusters{3}(:,1),Clusters{3}(:,2),Clusters{3}(:,3),‘g+’);
hold on;plot3(Clusters{4}(:,1),Clusters{4}(:,2),Clusters{4}(:,3),‘y*’);
grid on;hold off;
xlabel(‘波动率’);ylabel(‘偏度’);zlabel(‘峰度’);
set(gca,‘xlim’,[-5,5]);
title(‘四中心聚类图’);
%% k=5的聚类图
[~,Clusters,err3]=kmeansclustering(Samples,5);
subplot(2,2,3);
plot3(Clusters{1}(:,1),Clusters{1}(:,2),Clusters{1}(:,3),‘ro’);
hold on;plot3(Clusters{2}(:,1),Clusters{2}(:,2),Clusters{2}(:,3),‘b.’);
hold on;plot3(Clusters{3}(:,1),Clusters{3}(:,2),Clusters{3}(:,3),‘g+’);
hold on;plot3(Clusters{4}(:,1),Clusters{4}(:,2),Clusters{4}(:,3),‘y*’);
hold on;plot3(Clusters{5}(:,1),Clusters{5}(:,2),Clusters{5}(:,3),‘mx’);
grid on;hold off;
xlabel(‘波动率’);ylabel(‘偏度’);zlabel(‘峰度’);
set(gca,‘xlim’,[-5,5]);
title(‘五中心聚类图’);
%% k=6的聚类图
[~,Clusters,err4]=kmeansclustering(Samples,6);
subplot(2,2,4);
plot3(Clusters{1}(:,1),Clusters{1}(:,2),Clusters{1}(:,3),‘ro’);
hold on;plot3(Clusters{2}(:,1),Clusters{2}(:,2),Clusters{2}(:,3),‘b.’);
hold on;plot3(Clusters{3}(:,1),Clusters{3}(:,2),Clusters{3}(:,3),‘g+’);
hold on;plot3(Clusters{4}(:,1),Clusters{4}(:,2),Clusters{4}(:,3),‘y*’);
hold on;plot3(Clusters{5}(:,1),Clusters{5}(:,2),Clusters{5}(:,3),‘mx’);
hold on;plot3(Clusters{6}(:,1),Clusters{6}(:,2),Clusters{6}(:,3),‘cp’);
grid on;hold off;
xlabel(‘波动率’);ylabel(‘偏度’);zlabel(‘峰度’);
set(gca,‘xlim’,[-5,5]);
title(‘六中心聚类图’);
%% 画误差收敛图
figure;
subplot(2,2,1);plot(err1);xlabel(‘迭代次数’);ylabel(‘误差’);title(‘三中心聚类误差收敛图’);
set(gca,‘xlim’,[1,length(err1)]);
subplot(2,2,2);plot(err2);xlabel(‘迭代次数’);ylabel(‘误差’);title(‘四中心聚类误差收敛图’);
set(gca,‘xlim’,[1,length(err2)]);
subplot(2,2,3);plot(err3);xlabel(‘迭代次数’);ylabel(‘误差’);title(‘五中心聚类误差收敛图’);
set(gca,‘xlim’,[1,length(err3)]);

三、SOM聚类下的簇集特征

上文讨论了基于k-means方法的聚类，接下来我们讨论基于SOM神经网络方法的聚类效果。关于SOM神经网络的介绍和算法可参见这份博客
（https://www.cnblogs.com/sylvanas2012/p/5117056.html ），当然也可以通过百度搜索或相关书籍了解更多信息。对此，本文不展开详述。

接下来我们分别讨论一维和二维SOM神经网络下的聚类效果：

1）一维SOM网络
以1×10的网络为例，下图（左）给出了算法的收敛过程以及不同簇集下的平均收益率情况（右）。

从左图来看，在经过100次的迭代后尽管误差不断变小，但依然未达到收敛（考虑到该算法的计算量较大，预先设定了最大迭代次数）。不过尽管如此，此时的各簇集之间的收益率特征还是出现了明显区别，如右图所示。并且右图还反映了相邻簇集之间的收益率存在一定的相似性，这也与SOM网络的算法有关。

2）二维SOM网络
多数的SOM模型采用的都是二维网络，本文接下来进行同样的尝试，以下给出了矩形结构下8×8和6×6的网络聚类效果。

从上文的几次聚类效果来看，尽管都尚未取得完全的收敛，但不同簇集的收益率还是出现了分化，并且相邻组别的收益率大多存在一定的相似性。在下文中我们将以6×6网络的聚类效果为例进行回测。

本部分主要代码

1.SOM神经网络聚类算法
function [weight_renew,total_error]=somnn(Samples,network,total_ite,C1,eta)
% 输入参数 ：Samples：训练样本；network：网络结构；total_ite：迭代次数；C1：邻域范围参数；eta：学习率
% 输出参数：weight_renew：迭代后各节点的权值向量；total_error：误差
tic;
% 样本的标准化和归一化
Rvol=log(Samples(:,1)); Rskew=Samples(:,2); Rkurt=log(Samples(:,3));
stvol=(Rvol-mean(Rvol))/std(Rvol); stskew=(Rskew-mean(Rskew))/std(Rskew); stkurt=(Rkurt-mean(Rkurt))/std(Rkurt);
stsamples=[stvol,stskew,stkurt];
samples_norm=zeros(size(stsamples));
for i=1:size(stsamples,1)
samples_norm(i,:)=normalize0(stsamples(i,:));
end
weight_init=netinit(network,size(samples_norm,2));
% 对网络进行训练并统计每次迭代的误差
total_error=zeros(total_ite,1);
for i=1:total_ite
[weight_renew,te]=nettrain(samples_norm,weight_init,total_ite,i,C1,eta);
total_error(i)=te;
weight_init=weight_renew;
end
figure;
plot(total_error);
xlabel(‘迭代次数’);ylabel(‘误差’);
toc;
end
%% 归一化函数
function y=normalize0(x)
y=x./sum(x.^2);
end
%% 网络初始化
function weight_init=netinit(network,sd)
% 输入参数依次：网络结构，样本维度（即特征个数）
m=network(1); n=network(2);
weight_init=cell(m,n);
for i=1:m
for j=1:n
r=rand(1,sd)2-1; % 初始化权值限定在-1~1之间
weight_init{i,j}=normalize0®;
end
end
end
%% 网络训练
function [weight_renew,total_error]=nettrain(samples_norm,weight_init,total_ite,tem_ite,C1,eta)
% samples_norm：训练样本，weight_init：初始权值，total_ite：总迭代次数，tem_ite：当前迭代次数，C1：初始邻域范围
% weight_renew：训练（迭代）一次后的更新权值，total_error:当前网络的总误差
[m,n]=size(weight_init); % 网络结构
weight_renew=weight_init;
total_error=0;
for k=1:length(samples_norm);
distance=zeros(m,n);
for i=1:m
for j=1:n
distance(i,j)=sqrt(sum((samples_norm(k,:)-weight_init{i,j}).^2));
end
end
[min_d,min_idx]=min(distance();
total_error=total_error+min_d;
idx_col=ceil(min_idx/m); % 最佳适配点的列坐标
idx_row=min_idx-(idx_col-1)m; % 最佳适配点的行坐标
% neighbourhood=C1(1-tem_ite/total_ite); % 确定当前邻域范围
neighbourhood=C1exp(-3tem_ite/total_ite); % 以线性函数或指数函数收缩邻域范围，在试验中似乎指数函数的收敛性更好？
% 以下部分对于领域范围内的点进行权值更新
for i=1:m
for j=1:n
dist=sqrt((i-idx_row)^{2+(j-idx_col)}2);
if dist h=exp(-(dist/(0.5neighbourhood))^2);
weight_renew{i,j}=weight_init{i,j}+eta.h(samples_norm(k,:)-weight_init{i,j});
end
end
end
end
end

2.将样本按照训练好的SOM网络进行归类并统计每个簇集的特征
function [clusters_ret,mr,tt]=classifying2(Samples,weight)
% 基于som网络的分类
% clusters_ret：每个簇集的收益率集合，mr：平均收益率，tt：t检验结果
%% 标准化
Rvol=log(Samples(:,1)); Rskew=Samples(:,2); Rkurt=log(Samples(:,3)); Fret=Samples(:,4);
stvol=(Rvol-mean(Rvol))/std(Rvol); stskew=(Rskew-mean(Rskew))/std(Rskew); stkurt=(Rkurt-mean(Rkurt))/std(Rkurt);
stsamples=[stvol,stskew,stkurt];
samples_norm=zeros(size(stsamples));
for i=1:size(Samples,1)
samples_norm(i,:)=stsamples(i,:)./sum(stsamples(i,:).^2);
end
%% 归类
n=length(weight();
idx=zeros(length(Samples),1);
for k=1:length(samples_norm)
distance=zeros(n,1);
for i=1:n
distance(i)=sqrt(sum((samples_norm(k,:)-weight{i}).^2));
end
[~,minidx]=min(distance);
idx(k)=minidx;
end
clusters_ret=cell(size(weight));
mr=zeros(1,n);
for i=1:n
clusters_ret{i}=Fret(idx==i);
mr(i)=mean(clusters_ret{i});
end
% 计算各簇集之间t检验的p值
tt=zeros(n);
for i=1:n-1
for j=i+1:n
[~,p]=ttest2(clusters_ret{i},clusters_ret{j});
tt(i,j)=p;
end
end

四、样本外回测

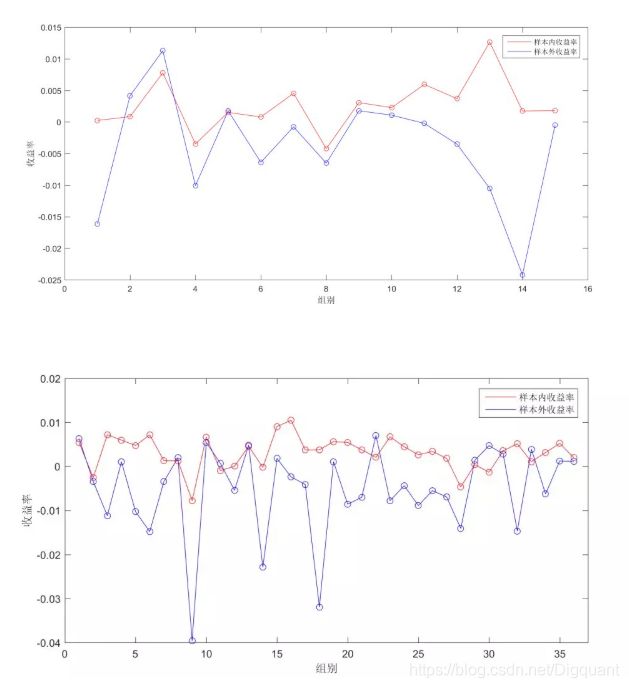
在前文中，我们分析了以2012-2015年为样本的三因子和收益率的规律，现将所得结论外推到样本外（2016年）进行回测。下面两张图依次给出了k=15时的k-means聚类下和6×6SOM网络聚类下的投资策略的回测结果。

投资策略具体描述为：计算过去5天10分钟频率下的三因子数据、标准化后与所有类别进行比较，并归类到最接近的类别，如果该类别的平均收益超过0.0055，则买入。5天换仓一次并且不考虑止损。

以上的回测效果显然并不让人满意。那么是否样本外推的时候出现的问题呢，我们进行了以下检验。用2016-2017年的数据在相同的规则下形成训练外样本，在样本内数据训练而成的集合类别中对样本外数据进行归类，然后比较相同类别下样本内和样本外的收益率。结果如下图所示。

从上面两张图的结果来看，很显然样本内和样本外差异巨大，这个结果无疑是令人失望的，这表明基于三因子历史数据的聚类结果并不能直接指导未来的投资。换而言之，尽管由三因子对收益率存在显著性的影响，但该影响可能是时变的，或者说不稳定的，并且基于历史数据的推断并不能直接预测未来。

当然，上述结果并不代表聚类分析方法之于选股策略的不适用，但前提是所选用的聚类因子具有良好的稳定性和可靠性，对此，还有待更进一步的研究。