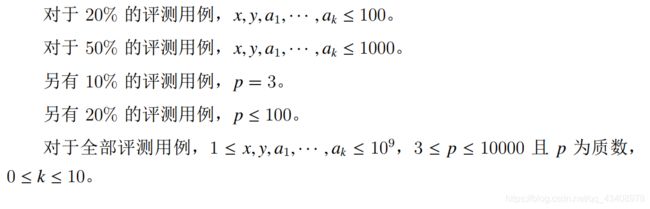2019第十届蓝桥杯大赛软件类B组C/C++国赛题解
2019第十届蓝桥杯大赛软件类B组C/C++国赛目录
-
-
- 试题 A：平方序列（结果填空）
- 试题 B：质数拆分（结果填空）
- 试题 C：拼接（结果填空）
- 试题 D：求值（结果填空）
- 试题 E：路径计数（结果填空）
- 试题 F： 最优包含（程序设计）
- 一个大佬写了下面题目的答案，点击下面链接
-
- 试题 G：排列数（程序设计）
- 试题 H：解密游戏（程序设计）
- 试题 I：第八大奇迹（程序设计）
- 试题 J：燃烧权杖（程序设计）
-
试题 A：平方序列（结果填空）
题意：
做法：双重循环暴力找一找，把N定义成了1e4（赌不会很大）。
代码：
#include答案：7020
试题 B：质数拆分（结果填空）
题意：
做法：有坑，我一开始以为是两个素数相加，其实可以是多个。先素数筛出2019以内的素数，然后可以转化成01背包求方案数，也可以用记忆化搜索。答案有很多种，记得开long long。
代码：
1、01背包求方案数：
#include2、记忆化搜索
#include答案：55965365465060
试题 C：拼接（结果填空）
题意：
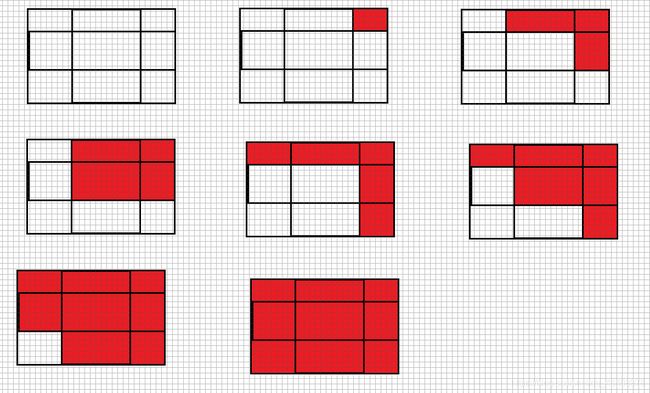
做法：要满足题目，分割方式必须是沿对角线对称之前想用dfs走到对角线的方式，写炸了，后来发现一个规律。首先右上角那一个必选（除了一种沿右边界分割的情况），第一行可以选1-7的格子，第二行能选1-6…并且右端一定靠近对角线，且下一行不能多余上一行，且连续。
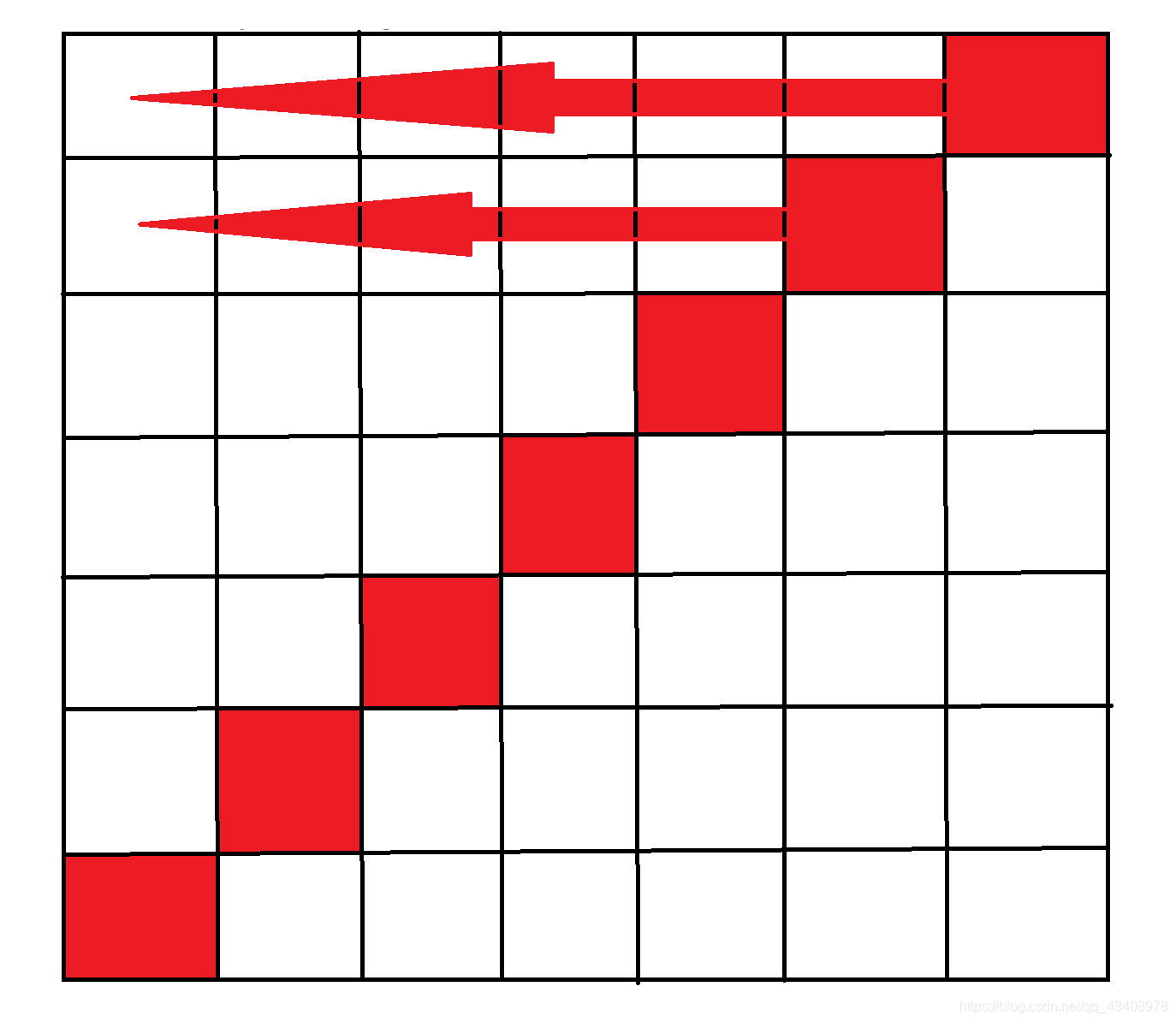
n=3时情况如下：
代码：
#include答案：128
试题 D：求值（结果填空）
题意：
做法：枚举到1e5，判断约数个数是否等于100。
代码：
#include答案：45360
试题 E：路径计数（结果填空）
题意：
做法：看成是6*6的方格，从(1,1)开始走，格子不能相交，问回到起点的路径有多少条。搜索。最后得减去(0,0)->(0,1)->(0,0)和(0,0)->(1,0)->(0,0)两种情况。
代码：
#include答案：206
——以下题目可以通过 AcWing 提交测试——
试题 F： 最优包含（程序设计）
题意：
做法：dp转移，dp[i][j]表示s[1:i]中要包含t[1:j]最少需要改变多少字母。
d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] , 当 s [ i ] = = s [ j ] m i n ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − 1 ] + 1 ) , 当 s [ i ] ! = s [ j ] dp[i][j] = \begin{cases} dp[i-1][j-1], 当s[i]==s[j] \\ min(dp[i-1][j], dp[i-1][j-1]+1), 当s[i]!=s[j] \end{cases} dp[i][j]={ dp[i−1][j−1],当s[i]==s[j]min(dp[i−1][j],dp[i−1][j−1]+1),当s[i]!=s[j]
代码：
#include——下面的题目因太菜做不出来，放一个题面和大佬们的思路叭——
一个大佬写了下面题目的答案，点击下面链接
点击这里
试题 G：排列数（程序设计）
题意：
做法：好像大部分是全排列暴力拿前20分，看到某大佬在写着dp正解。
试题 H：解密游戏（程序设计）
题意：
做法：貌似是找规律？模4的’g’？
试题 I：第八大奇迹（程序设计）
题意：
做法：树套树？现场手搓的都是大佬。
试题 J：燃烧权杖（程序设计）
题意：
