字符串相似度算法(编辑距离算法 Levenshtein Distance)
在搞验证码识别的时候需要比较字符代码的相似度用到“编辑距离算法”,关于原理和C#实现做个记录。
据百度百科介绍:
编辑距离,又称Levenshtein距离(也叫做Edit Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将kitten一字转成sitting:
sitten (k→s)
sittin (e→i)
sitting (→g)
俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。因此也叫Levenshtein Distance。
例如
- 如果str1="ivan",str2="ivan",那么经过计算后等于 0。没有经过转换。相似度=1-0/Math.Max(str1.length,str2.length)=1
- 如果str1="ivan1",str2="ivan2",那么经过计算后等于1。str1的"1"转换"2",转换了一个字符,所以距离是1,相似度=1-1/Math.Max(str1.length,str2.length)=0.8
应用
DNA分析
拼字检查
语音辨识
抄袭侦测
感谢大石头在评论中给出一个很好的关于此方法应用的连接 补充在此:
小规模的字符串近似搜索,需求类似于搜索引擎中输入关键字,出现类似的结果列表,文章连接:【算法】字符串近似搜索
算法过程
- str1或str2的长度为0返回另一个字符串的长度。 if(str1.length==0) return str2.length; if(str2.length==0) return str1.length;
- 初始化(n+1)*(m+1)的矩阵d,并让第一行和列的值从0开始增长。
- 扫描两字符串(n*m级的),如果:str1[i] == str2[j],用temp记录它,为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。
- 扫描完后,返回矩阵的最后一个值d[n][m]即是它们的距离。
计算相似度公式:1-它们的距离/两个字符串长度的最大值。
为了直观表现,我将两个字符串分别写到行和列中,实际计算中不需要。我们用字符串“ivan1”和“ivan2”举例来看看矩阵中值的状况:
1、第一行和第一列的值从0开始增长
| i | v | a | n | 1 | ||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| i | 1 | |||||
| v | 2 | |||||
| a | 3 | |||||
| n | 4 | |||||
| 2 | 5 |
2、i列值的产生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1 ; Matrix[i - 1, j - 1] + t
| i | v | a | n | 1 | ||
| 0+t=0 | 1+1=2 | 2 | 3 | 4 | 5 | |
| i | 1+1=2 | 取三者最小值=0 | ||||
| v | 2 | 依次类推:1 | ||||
| a | 3 | 2 | ||||
| n | 4 | 3 | ||||
| 2 | 5 | 4 |
3、V列值的产生
| i | v | a | n | 1 | ||
| 0 | 1 | 2 | ||||
| i | 1 | 0 | 1 | |||
| v | 2 | 1 | 0 | |||
| a | 3 | 2 | 1 | |||
| n | 4 | 3 | 2 | |||
| 2 | 5 | 4 | 3 |
依次类推直到矩阵全部生成
| i | v | a | n | 1 | ||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| i | 1 | 0 | 1 | 2 | 3 | 4 |
| v | 2 | 1 | 0 | 1 | 2 | 3 |
| a | 3 | 2 | 1 | 0 | 1 | 2 |
| n | 4 | 3 | 2 | 1 | 0 | 1 |
| 2 | 5 | 4 | 3 | 2 | 1 | 1 |
最后得到它们的距离=1
相似度:1-1/Math.Max(“ivan1”.length,“ivan2”.length) =0.8
算法用C#实现
public class LevenshteinDistance
{
/// <summary>
/// 取最小的一位数
/// </summary>
/// <param name="first"></param>
/// <param name="second"></param>
/// <param name="third"></param>
/// <returns></returns>
private int LowerOfThree(int first, int second, int third)
{
int min = Math.Min(first, second);
return Math.Min(min, third);
}
private int Levenshtein_Distance(string str1, string str2)
{
int[,] Matrix;
int n = str1.Length;
int m = str2.Length;
int temp = 0;
char ch1;
char ch2;
int i = 0;
int j = 0;
if (n == 0)
{
return m;
}
if (m == 0)
{
return n;
}
Matrix = new int[n + 1, m + 1];
for (i = 0; i <= n; i++)
{
//初始化第一列
Matrix[i, 0] = i;
}
for (j = 0; j <= m; j++)
{
//初始化第一行
Matrix[0, j] = j;
}
for (i = 1; i <= n; i++)
{
ch1 = str1[i - 1];
for (j = 1; j <= m; j++)
{
ch2 = str2[j - 1];
if (ch1.Equals(ch2))
{
temp = 0;
}
else
{
temp = 1;
}
Matrix[i, j] = LowerOfThree(Matrix[i - 1, j] + 1, Matrix[i, j - 1] + 1, Matrix[i - 1, j - 1] + temp);
}
}
for (i = 0; i <= n; i++)
{
for (j = 0; j <= m; j++)
{
Console.Write(" {0} ", Matrix[i, j]);
}
Console.WriteLine("");
}
return Matrix[n, m];
}
/// <summary>
/// 计算字符串相似度
/// </summary>
/// <param name="str1"></param>
/// <param name="str2"></param>
/// <returns></returns>
public decimal LevenshteinDistancePercent(string str1, string str2)
{
//int maxLenth = str1.Length > str2.Length ? str1.Length : str2.Length;
int val = Levenshtein_Distance(str1, str2);
return 1 - (decimal)val / Math.Max(str1.Length, str2.Length);
}
}
|
1
|
<strong>调用</strong>
|
static void Main(string[] args)
{
string str1 = "ivan1";
string str2 = "ivan2";
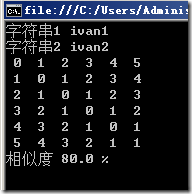
Console.WriteLine("字符串1 {0}", str1);
Console.WriteLine("字符串2 {0}", str2);
Console.WriteLine("相似度 {0} %", new LevenshteinDistance().LevenshteinDistancePercent(str1, str2) * 100);
Console.ReadLine();
}
|
1
|
<strong>结果</strong>
|
http://www.cnblogs.com/ivanyb/archive/2011/11/25/2263356.html