图像处理(十四)图像分割(4)grab cut的图割实现-Siggraph 2004
grab cut图像分割
原文地址:http://blog.csdn.net/hjimce/article/details/45932569
作者:hjimce
Grab cut算法是2004年才有的算法,自从这个算法出来,在交互是图像分割领域影响极其深刻,目前文献《“GrabCut” — Interactive Foreground Extraction using Iterated Graph Cuts》的引用率真不是一般的高,于是图论分割的算法就有很多新算法出现了,还有什么Normarlized Cut 、One cut,但是大体的思路大同小异。
我第一次学这个算法是在半年前,当时对于高斯混合建模理解的不是很透彻,然后又有Max flow 也不懂,而项目也催的很紧急,所以这个算法当时给我的印象是“好难”。最后只是把图像分割之(二)Graph Cut(图割)这位哥们的博客看了一下,然后思路迷迷糊糊的,不过很感谢他让我学会了grab cut 算法。现在回想起来其实这个算法也不过如此,好了废话不多说,我这里主要结合opencv的grab cut 代码进行讲解,同时参考图像分割之(三)从Graph Cut到Grab Cut 的博文,进行解说grab cut 过程实现流程。不打算将理论的东西,因为理论总是看起来很深奥的样子,其实有时候十几页的理论,就是几行代码的事。
如果你想把原版grab cut代码自己写过一遍,那么需要对以下基础知识非常熟悉:
1、k均值聚类
1、高斯混合模型建模
2、max flow/min cut
一、算法流程
输入:图像、被标记好的前景、背景
输出:分割图像
其中输入的前景、背景指的是一种概率,如果你已经明确某一块区域是背景,那么它属于背景的概率为1;当然如果你觉得它有可能背景,但是没有百分百的肯定,这个时候你就要用到高斯模型,对其进行建模,然后估算概率,这也正是文献的精髓部分。现在我以下图为例,用户通过交互输入框选区域,前景位于框选区域内,也就是说矩形区域外的全部属于背景,且概率为百分百。然后方框内可能属于前景,概率需要用高斯混合建模求解。
其大体算法流程如下:
1、用户交互输入矩形结果,初始化。
/*
由用户输入的矩形外面 全部标记为一定是背景
矩形内部标记为 可能是前景
*/
void GrabCut::initMaskWithRect( Eigen::MatrixXf& mask, CRect rect )
{
mask.resize(m_Image->Height,m_Image->Width);
mask.setZero();
for (int i=rect.TopLeft().y;i2、建模阶段。根据被标记的信息对前景和背景进行分别高斯混合模型建模。过程大体是先通过k均值进行初始化聚类,然后根据聚类结果,计算每个类的高斯模型参数
/*
通过k均值进行聚类 然后根据聚类结果的各类进行高斯建模
*/
//mask为由用户交互输入的信息
//GC_BGD表示确定为背景 GC_PR_BGD表示可能为背景,也就是属于背景的概率比较大
//GCD_FGD表示确定是前景 GCD_PR_FGD表示可能为前景即前景的概率比较大
void GrabCut::initGMMs(const Eigen::MatrixXf& mask, GMM& bgdGMM, GMM& fgdGMM )
{
int height=m_Image->Height;
int width=m_Image->Width;
const int kMeansItCount = 10; //k均值聚类最大迭代次数
const int kMeansType = cv::KMEANS_PP_CENTERS;
cv::Mat bgdLabels, fgdLabels; //聚类结果标号存储
vector bgdSamples, fgdSamples;
CPoint p;
for( p.y = 0; p.y (i,0),Eigen::Vector3f(bgdSamples[i][0],bgdSamples[i][1],bgdSamples[i][2]) );
bgdGMM.endLearning();
//根据k均值聚类结果,对每个前景中的高斯混合模型类进行高斯建模
fgdGMM.initLearning();
for( int i = 0; i < (int)fgdSamples.size(); i++ )
fgdGMM.addSample( fgdLabels.at(i,0),Eigen::Vector3f(fgdSamples[i][0],fgdSamples[i][1],fgdSamples[i][2]));
fgdGMM.endLearning();
} 高斯混合模型建模相关函数:
//相关高斯模型参数初始化,可放在析构函数中
void GMM::initLearning()
{
for( int ci = 0; ci < componentsCount; ci++)
{
sums[ci][0] = sums[ci][1] = sums[ci][2] = 0;
prods[ci][0][0] = prods[ci][0][1] = prods[ci][0][2] = 0;
prods[ci][1][0] = prods[ci][1][1] = prods[ci][1][2] = 0;
prods[ci][2][0] = prods[ci][2][1] = prods[ci][2][2] = 0;
sampleCounts[ci] = 0;
}
totalSampleCount = 0;
}
//根据k均值的聚类标记 计算每个高斯模型的均值及其协方差矩阵
//外部调用
void GMM::addSample( int ci, const Eigen::Vector3f color )
{
sums[ci][0] += color[0]; sums[ci][1] += color[1]; sums[ci][2] += color[2];
prods[ci][0][0] += color[0]*color[0]; prods[ci][0][1] += color[0]*color[1]; prods[ci][0][2] += color[0]*color[2];
prods[ci][1][0] += color[1]*color[0]; prods[ci][1][1] += color[1]*color[1]; prods[ci][1][2] += color[1]*color[2];
prods[ci][2][0] += color[2]*color[0]; prods[ci][2][1] += color[2]*color[1]; prods[ci][2][2] += color[2]*color[2];
sampleCounts[ci]++;
totalSampleCount++;
}
//外部调用,结束学习
void GMM::endLearning()
{
const float variance = 0.01;
for( int ci = 0; ci < componentsCount; ci++ )
{
int n = sampleCounts[ci]; //第ci个高斯模型的样本像素个数
if( n == 0 )
coefs[ci] = 0;
else
{
//计算第ci个高斯模型的权值系数 ,也就是这个属于这个类的像素点数占总数的百分比
coefs[ci] = (float)n/totalSampleCount;
//计算第ci个高斯模型的均值
float* m = mean + 3*ci;
m[0] = sums[ci][0]/n; m[1] = sums[ci][1]/n; m[2] = sums[ci][2]/n;
//计算协方差矩阵结果
float* c = cov + 9*ci;
c[0] = prods[ci][0][0]/n - m[0]*m[0]; c[1] = prods[ci][0][1]/n - m[0]*m[1]; c[2] = prods[ci][0][2]/n - m[0]*m[2];
c[3] = prods[ci][1][0]/n - m[1]*m[0]; c[4] = prods[ci][1][1]/n - m[1]*m[1]; c[5] = prods[ci][1][2]/n - m[1]*m[2];
c[6] = prods[ci][2][0]/n - m[2]*m[0]; c[7] = prods[ci][2][1]/n - m[2]*m[1]; c[8] = prods[ci][2][2]/n - m[2]*m[2];
//计算协方差矩阵行列式
float dtrm = c[0]*(c[4]*c[8]-c[5]*c[7]) - c[1]*(c[3]*c[8]-c[5]*c[6]) + c[2]*(c[3]*c[7]-c[4]*c[6]);
if( dtrm <= std::numeric_limits::epsilon() )
{
c[0] += variance;
c[4] += variance;
c[8] += variance;
}
//计算第ci个高斯模型的协方差的逆Inverse和行列式Determinant
calcInverseCovAndDeterm(ci);
}
}
}
//计算第ci个高斯模型的协方差逆矩阵,及其行列式 这个是为了后面计算高斯概率方便
void GMM::calcInverseCovAndDeterm( int ci )
{
if( coefs[ci] > 0 )
{
//第ci个高斯模型协方差
float *c = cov + 9*ci;
float dtrm =
covDeterms[ci] = c[0]*(c[4]*c[8]-c[5]*c[7]) - c[1]*(c[3]*c[8]-c[5]*c[6])
+ c[2]*(c[3]*c[7]-c[4]*c[6]);
float fa= std::numeric_limits::epsilon();
ASSERT( dtrm > std::numeric_limits::epsilon() );
//矩阵求逆公式
inverseCovs[ci][0][0] = (c[4]*c[8] - c[5]*c[7]) / dtrm;
inverseCovs[ci][1][0] = -(c[3]*c[8] - c[5]*c[6]) / dtrm;
inverseCovs[ci][2][0] = (c[3]*c[7] - c[4]*c[6]) / dtrm;
inverseCovs[ci][0][1] = -(c[1]*c[8] - c[2]*c[7]) / dtrm;
inverseCovs[ci][1][1] = (c[0]*c[8] - c[2]*c[6]) / dtrm;
inverseCovs[ci][2][1] = -(c[0]*c[7] - c[1]*c[6]) / dtrm;
inverseCovs[ci][0][2] = (c[1]*c[5] - c[2]*c[4]) / dtrm;
inverseCovs[ci][1][2] = -(c[0]*c[5] - c[2]*c[3]) / dtrm;
inverseCovs[ci][2][2] = (c[0]*c[4] - c[1]*c[3]) / dtrm;
}
}
3、概率计算。OK,到了这一步,可以说已经完成了算法的上半部分,我们得到的结果是:
a、前景的高斯混合模型(原paper中选择聚类成5个),其包含5个单高斯模型的相关参数,每个单高斯模型包含三个参数:均值、协方差矩阵、此模型所占的比例权重(这个参数是根据k均值聚类后,计算每个类的像素点个数占总数的比例:
coefs[ci] = (float)n/totalSampleCount; 其它参数,什么协方差矩阵的逆矩阵、行列式值只是为了计算方便而进行存储,根据协方差矩阵就可以把这两个参数计算出来。
b、与前景一样,对背景建模后的5个高斯模型的相关参数。
因为我们的模型前景及背景的高斯混合模型已经建立完毕,现在我假设,如果给定一点像素点的color值,那么我们可以很快的计算出其分别属于前景及背景的概率,计算公式如下
也就是把像素点p(x,y)属于某个高斯成分的概率与该成分的权重的乘积,最后进行累加。
//输入像素点的颜色值 计算其在高斯混合模型中的总概率和
float GMM::operator()( const Eigen::Vector3f color ) const
{
float res = 0;
for( int ci = 0; ci < componentsCount; ci++ )
res += coefs[ci] * (*this)(ci, color ); //component权重与该像素点属于这个component概率相乘
return res;
}
//计算像素点颜色值color ,属于第ci个高斯模型的概率
float GMM::operator()( int ci, const Eigen::Vector3f color ) const
{
float res = 0;
if( coefs[ci] > 0 )
{
ASSERT( covDeterms[ci] > std::numeric_limits::epsilon() );
Eigen::Vector3f diff = color;
float* m = mean + 3*ci;
diff[0] -= m[0]; diff[1] -= m[1]; diff[2] -= m[2];
float mult = diff[0]*(diff[0]*inverseCovs[ci][0][0] + diff[1]*inverseCovs[ci][1][0] + diff[2]*inverseCovs[ci][2][0])
+ diff[1]*(diff[0]*inverseCovs[ci][0][1] + diff[1]*inverseCovs[ci][1][1] + diff[2]*inverseCovs[ci][2][1])
+ diff[2]*(diff[0]*inverseCovs[ci][0][2] + diff[1]*inverseCovs[ci][1][2] + diff[2]*inverseCovs[ci][2][2]);
res = 1.0f/sqrt(covDeterms[ci]) * exp(-0.5f*mult);
}
return res;
} 因为后面就是要计算被标记为GC_PR_BGD、 GC_PR_FGD的概率,所以你可以把这些像素点分别属于前景模型及背景模型的概率计算出来,并存储起来,后面将用这玩意进行图的构建。
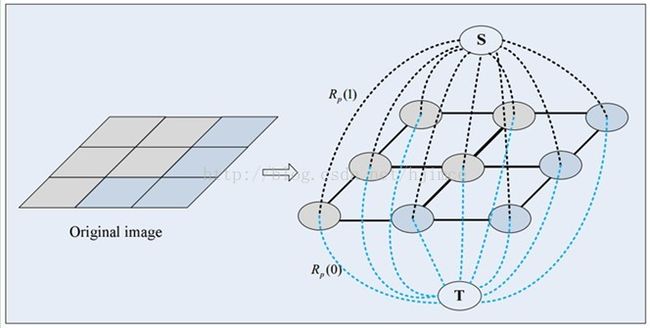
4、图的构建。这一步要用到图论的一些简单知识,其中最主要的算法当然是max flow /min cut 了。如下图,其中s代表前景,t代表背景,这两个点是为了进行图割,人为的加进去的两个顶点,也就是说假设图片为3*3大小的图片,其共有9个像素点,那么加上s、t两个点,最后我们构建的图就有11个顶点。
这个图有两种边:
第一种边:每两个邻接像素点间会有一条边,而这条边的长度(流、权重)就是这两个像素点的颜色差值。
//图的第一种边长,相邻像素点间的边长计算,这个函数是直接求取像素点的4邻域像素点与该像素点的像素差值模长(opencv采用的是高斯函数)
//gamma可以理解为一个权重系数,或者说是一个归一化系数(当然不是真正的归一哈)
//,这是因为我们通过高斯混合模型计算的概率值是0~1的值,然而相邻像素点每个通道就有0~255,这样计算出来的边长是0~255*255*255,
//因此我们必须让这个根据像素值构建的边进行合适的缩放,
//不然高斯概率取值范围最大也才为1,也就是第二种边的长度最长也才为1,相对于255*255*255,这个简直没法活了
void GrabCut::calcNWeights(Eigen::MatrixXf& leftW, Eigen::MatrixXf& upleftW, Eigen::MatrixXf& upW,
Eigen::MatrixXf& uprightW, float beta, float gamma )
{
const float gammaDivSqrt2 = gamma / std::sqrt(2.0f);
//每个方向的边的权值通过一个和图大小相等的Eigen::MatrixXf来保存
int height=m_Image->Height;
int width=m_Image->Width;
leftW.resize(height,width);
upleftW.resize(height,width);;
upW.resize(height,width);;
uprightW.resize(height,width);;
for( int y = 0; y =0 )
{
Eigen::Vector3f diff = color -GetPiexl(CPoint(x-1,y),m_Image);
leftW(y,x) = gamma * exp(-beta*diff.dot(diff)); //高斯函数又来了,计算距离权重的神器
}
else
leftW(y,x) = 0;
if( x-1>=0 && y-1>=0 )
{
Eigen::Vector3f diff = color -GetPiexl(CPoint(x-1,y-1),m_Image);
upleftW(y,x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
upleftW(y,x) = 0;
if( y-1>=0 ) // up
{
Eigen::Vector3f diff = color -GetPiexl(CPoint(x,y-1),m_Image);
upW(y,x) = gamma * exp(-beta*diff.dot(diff));
}
else
upW(y,x) = 0;
if( x+1=0 ) // upright
{
Eigen::Vector3f diff = color - GetPiexl(CPoint(x+1,y-1),m_Image);
uprightW(y,x) = gammaDivSqrt2 * exp(-beta*diff.dot(diff));
}
else
uprightW(y,x) = 0;
}
}
} 第二种边:也就是我们第3步计算每个像素点属于前景、背景的概率。s(前景)到每个像素点p的连接边,就是p点属于s的概率。t(背景)到每个像素点p的连接边,也就是p点属于t的概率。这些我们在第3步就已经可以计算好了,也就是前面的所有步骤中,其实都只是为了计算s、t分别到每个像素顶点的连接边的长度而已。
图的具体构建函数为:
//图的构建 输入参数包括:交互输入的mask,前面高斯建模的结果bgdGMM、fgdGMM。
//lambda为调节参数,可以理解为无穷大的数,用于连接被标记为GC_BGD、GC_FGD的长度,因为这两个是已经确定的
//所以我们自然而然要在后面的图割中,把GC_BGD分割给背景t,把GC_FGD分割给前景s,这就是为什么这个数为无穷大的原因了
//leftW、upleftW、upW、uprightW存储了第一类边长
//输出:graph
void GrabCut::constructGCGraph(const Eigen::MatrixXf& mask, const GMM& bgdGMM, const GMM& fgdGMM, float lambda,
const Eigen::MatrixXf& leftW, const Eigen::MatrixXf& upleftW, const Eigen::MatrixXf& upW, const Eigen::MatrixXf& uprightW,
GCGraph& graph )
{
int vtxCount = m_Image->Height*m_Image->Width; //图顶点个数
int edgeCount = 2*(4*vtxCount - 3*(m_Image->Width + m_Image->Height) + 2); //图边数计算
graph.create(vtxCount, edgeCount); //根据顶点个数、边数,先初始化构建一个图,所得简单点就是先分配好内存
CPoint p;
int heigth=m_Image->Height;
int width=m_Image->Width;
for( p.y = 0; p.y 0 )
{
float w = leftW(p.y,p.x);
graph.addEdges( vtxIdx, vtxIdx-1, w, w );
}
if( p.x>0 && p.y>0 )
{
float w = upleftW(p.y,p.x);
graph.addEdges( vtxIdx, vtxIdx-width-1, w, w );
}
if( p.y>0 )
{
float w = upW(p.y,p.x);
graph.addEdges( vtxIdx, vtxIdx-width, w, w );
}
if( p.x0 )
{
float w = uprightW(p.y,p.x);
graph.addEdges( vtxIdx, vtxIdx-width+1, w, w );
}
}
}
} 5、图割与更新标记阶段。根据上面构建的图,进行最大流/最小割。个人感觉最大流/最小割跟最短路径Dijkstra算法很像,只要很熟悉Dijkstra算法,那么写max flow算法不是什么难事,不过我自己写的代码当然比不上大牛写的代码,高手都是用了各种数据结构写的,速度杠杠的,我这种菜鸟写出来的速度,慢了别人几倍。所以如果想要用,直接用opencv的,才是王道
//max flow进行图割、并更新mask函数
//graph就是我们上一步构建的图
void GrabCut::estimateSegmentation( GCGraph& graph, Eigen::MatrixXf& mask )
{
graph.maxFlow(); //图割 将把图分割成两部分
CPoint p;
for( p.y = 0; p.y 图割完以后,我们可以把图片的像素点归为两类,一类被s给割走了,一类被t给割走了,被s给割走,那么它就相当于属于s(前景),被t给割走那么它就相当属于背景了。因此割完以后,我们需要更新那些不确定属于前景还是背景的点的标号。
到了这里可以说算法已经结束了,接着就只是迭代的事了,你可以选择只迭代一次,就万事大吉,图割学习完毕了。贴一下结果:
最后要说的一句是:原版的grab cut 算法分割很粗糙,而且速度很慢,后面许多大牛,对这篇文献做了相关的改进,还有一大堆效果非常好的改进的grab cut 算法等着我们去学习。
*************作者:hjimce 联系qq:1393852684 更多资源请关注我的博客:http://blog.csdn.net/hjimce 原创文章,转载请保留本行信息*********
参考文献:
1、“GrabCut” — Interactive Foreground Extraction using Iterated Graph Cuts
2、http://blog.csdn.net/zouxy09/article/details/8532111
3、Opencv