Python深度学习——卷积神经网络简介
文章目录
-
-
- 1.使用CNN对MNIST 数字进行分类
- 2.卷积运算
- 3.最大池化运算
-
卷积神经网络,也叫convnet,它是计算机视觉应用几乎都在使用的一种深度学习模型。
1.使用CNN对MNIST 数字进行分类
下列代码将会展示一个简单的卷积神经网络。
(1)Conv2D 层和MaxPooling2D 层的堆叠
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
目前卷积神经网络的架构:
- 输入张量:卷积神经网络接收形状为
(image_height, image_width, image_channels)的输入张量(不包括批量维度)。本例中设置卷积神经网络处理大小为(28, 28, 1) 的输入张量,这正是MNIST 图像的格式。我们向第一层传入参数input_shape=(28, 28, 1) 来完成此设置。 - 卷积层和池化层的输出张量:每个Conv2D 层和MaxPooling2D 层的输出都是一个形状为
(height, width,channels)的3D 张量。宽度和高度两个维度的尺寸通常会随着网络加深而变小。通道数量由传入Conv2D 层的第一个参数所控制(32 或64)。
(2)Dense层的堆叠
我们需要将最后的输出张量[大小为(3, 3, 64)]输入到一个密集连接分类器网络中,即Dense 层的堆叠。这些分类器可以处理1D 向量,而当前的输出是3D 张量。首先,我们需要将3D 输出展平为1D,然后在上面添加几个Dense 层。
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))

在进入两个Dense 层之前,形状(3, 3, 64) 的输出被展平为形状(576,) 的向量。我们将进行10 类别分类,最后一层使用带10 个输出的softmax 激活。
在MNIST数据集上,第2 章密集连接网络的测试精度为97.8%,但这个简单卷积神经网络的测试精度达到了99.3%,我们将错误率降低了68%(相对比例)。与密集连接模型相比,这个简单卷积神经网络的效果显然要更好。
2.卷积运算
(1)密集连接层和卷积层的区别
密集连接层和卷积层的根本区别在于,Dense 层从输入特征空间中学到的是全局模式(比如对于MNIST 数字,全局模式就是涉及所有像素的模式),而卷积层学到的是局部模式。对于图像来说,学到的就是在输入图像的二维小窗口中发现的模式。在上面的例子中,这些窗口的大小都是3×3。
这个重要特性使卷积神经网络具有以下两个性质:
- 卷积神经网络学到的模式具有平移不变性(translation invariant)。这使得卷积神经网络在处理图像时可以高效利用数据(视觉世界从根本上具有平移不变性),它只需要更少的训练样本。
- 卷积神经网络可以学到模式的空间层次结构(spatial hierarchies of patterns)。这使得卷积神经网络可以有效地学习越来越复杂、越来越抽象的视觉概念(视觉世界从根本上具有空间层次结构)。
(2)卷积层的工作原理
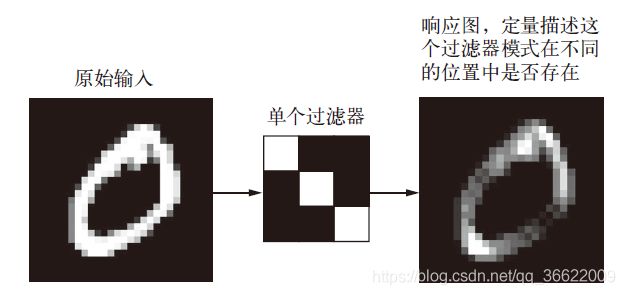
对于包含两个空间轴(高度和宽度)和一个深度轴(也叫通道轴)的3D 张量,其卷积也叫特征图(feature map)。对于RGB 图像,深度轴的维度为3。对于黑白图像,深度为1。卷积运算从输入特征图中提取图块,并对所有这些图块应用相同的变换,生成输出特征图(output feature map)。该输出特征图仍是一个3D 张量,具有宽度和高度,其深度可以任意取值,因为输出深度是层的参数,深度轴的不同通道不再代表特定颜色,而是代表过滤器(filter)。过滤器对输入数据的某一方面进行编码,比如,单个过滤器可以从更高层次编码这样一个概念:“输入中包含一张脸。”
在MNIST 示例中,第一个卷积层接收一个大小为(28, 28, 1) 的特征图,并输出一个大小为(26, 26, 32) 的特征图,即它在输入上计算32 个过滤器。对于这32 个输出通道,每个通道都包含一个26×26 的数值网格,它是过滤器对输入的响应图(response map),表示这个过滤器模式在输入中不同位置的响应。这也是特征图这一术语的含义:深度轴的每个维度都是一个特征(或过滤器),而2D 张量output[:, :, n] 是这个过滤器在输入上的响应的二维空间图(map)。
卷积由以下两个关键参数所定义。
- 从输入中提取的图块尺寸:这些图块的大小通常是 3×3 或 5×5。本例中为 3×3,这是很常见的选择。
- 输出特征图的深度:卷积所计算的过滤器的数量。本例第一层的深度为32,最后一层的深度是64。
对于Keras 的Conv2D 层,这些参数都是向层传入的前几个参数:Conv2D(output_depth,(window_height, window_width))。
(3)卷积运算的具体过程
在3D 输入特征图上滑动(slide)这些3×3 或5×5 的窗口,在每个可能的位置停止并提取周围特征的3D 图块[形状为(window_height, window_width, input_depth)]。然后每个3D 图块与学到的同一个权重矩阵[叫作卷积核(convolution kernel)]做张量积,转换成形状为(output_depth,)的1D 向量。然后对所有这些向量进行空间重组,使其转换为形状为(height, width, output_depth) 的3D 输出特征图。输出特征图中的每个空间位置都对应于输入特征图中的相同位置(比如输出的右下角包含了输入右下角的信息)。举个例子,利用3×3 的窗口,向量output[i, j, :] 来自3D 图块input[i-1:i+1,j-1:j+1, :]。
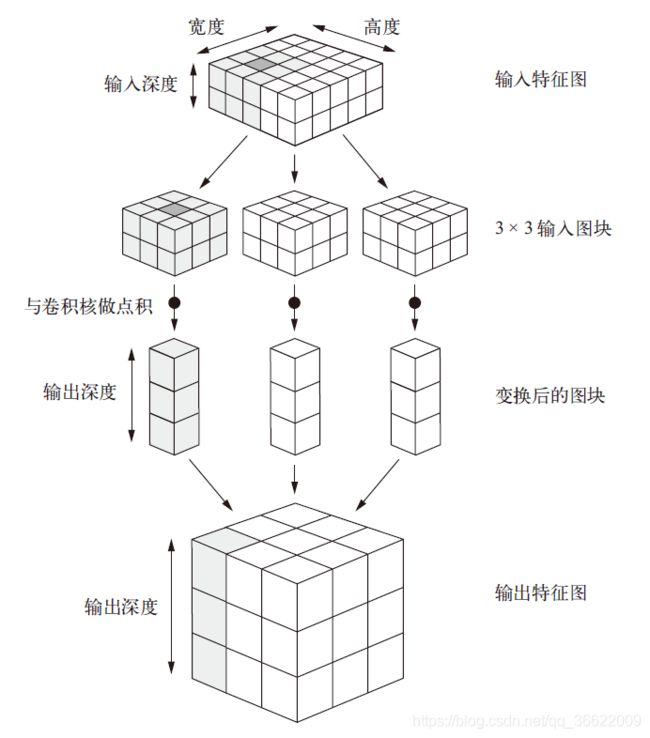
注意,输出的宽度和高度可能与输入的宽度和高度不同。不同的原因可能有两点。
- 边界效应,可以通过对输入特征图进行填充来抵消。
- 使用了步幅(stride)。
(4)边界效应与填充
假设有一个5×5 的特征图(共25 个方块)。其中只有9 个方块可以作为中心放入一个3×3 的窗口,这9 个方块形成一个3×3 的网格。因此,输出特征图的尺寸是3×3。它比输入尺寸小了一点,在本例中沿着每个维度都正好缩小了2 个方块。在前一个例子中你也可以看到这种边界效应的作用:开始的输入尺寸为28×28,经过第一个卷积层之后尺寸变为26×26。
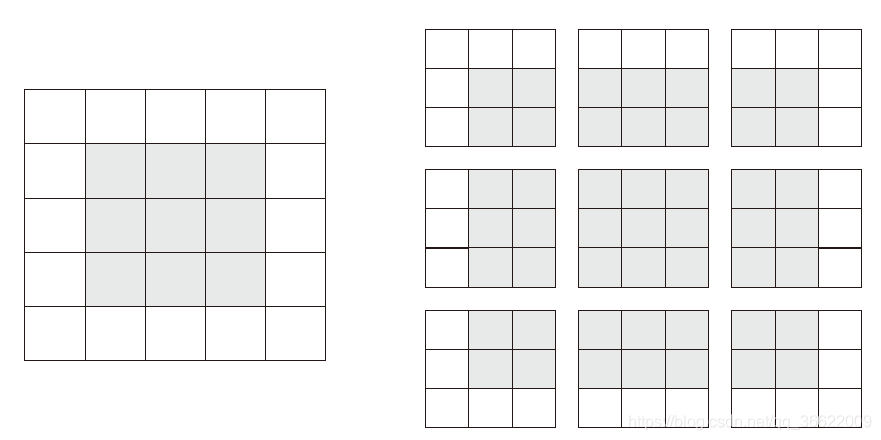
如果你希望输出特征图的空间维度与输入相同,那么可以使用填充(padding)。填充是在输入特征图的每一边添加适当数目的行和列,使得每个输入方块都能作为卷积窗口的中心。对于3×3 的窗口,在左右各添加一列,在上下各添加一行。对于5×5 的窗口,各添加两行和两列。
对于Conv2D 层,可以通过padding 参数来设置填充,这个参数有两个取值:valid 表示不使用填充(只使用有效的窗口位置);same 表示“填充后输出的宽度和高度与输入相同”。padding 参数的默认值为valid。
(5)卷积步幅
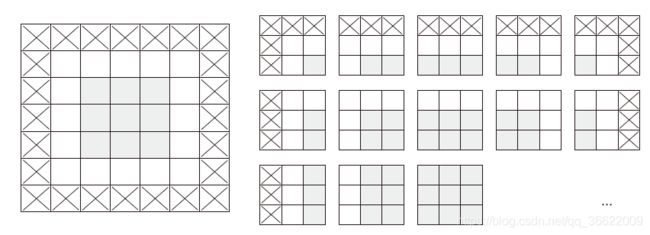
影响输出尺寸的另一个因素是步幅的概念。目前为止,对卷积的描述都假设卷积窗口的中心方块都是相邻的。但两个连续窗口的距离是卷积的一个参数,叫作步幅,默认值为1。也可以使用步进卷积(strided convolution),即步幅大于1 的卷积。在下图中,你可以看到用步幅为2 的3×3 卷积从5×5 输入中提取的图块(无填充)。
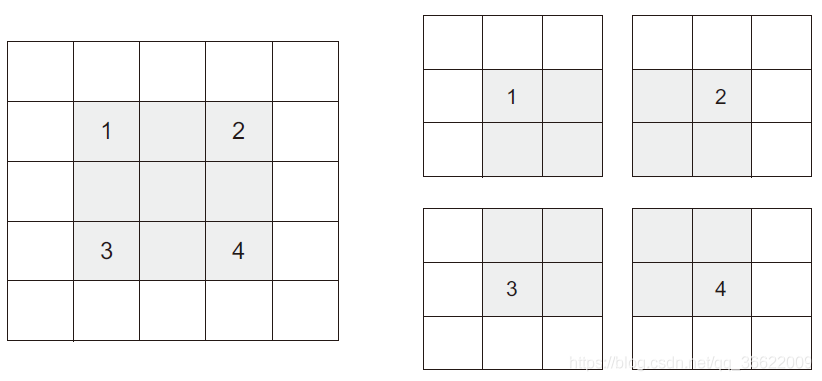
步幅为2 意味着特征图的宽度和高度都被做了2 倍下采样(除了边界效应引起的变化)。虽然步进卷积对某些类型的模型可能有用,但在实践中很少使用。为了对特征图进行下采样,我们不用步幅,而是通常使用最大池化(max-pooling)运算。
3.最大池化运算
在卷积神经网络示例中,每个MaxPooling2D 层之后,特征图的尺寸都会减半。例如,在第一个MaxPooling2D 层之前,特征图的尺寸是26×26,但最大池化运算将其减半为13×13。这就是最大池化的作用:对特征图进行下采样,与步进卷积类似。
最大池化是从输入特征图中提取窗口,并输出每个通道的最大值。它的概念与卷积类似,
但是最大池化使用硬编码的max 张量运算对局部图块进行变换,而不是使用学到的线性变换(卷积核)。最大池化与卷积的最大不同之处在于,最大池化通常使用2×2 的窗口和步幅2,其目的是将特征图下采样2 倍。与此相对的是,卷积通常使用3×3 窗口和步幅1。
使用下采样的原因:
- 减少需要处理的特征图的元素个数。
- 通过让连续卷积层的观察窗口越来越大(即窗口覆盖原始输入的比例越来越大),从而引入空间过滤器的层级结构。
最大池化不是实现这种下采样的唯一方法。除了使用步幅来实现,还可以使用平均池化来代替最大池化,其方法是将每个局部输入图块变换为取该图块各通道的平均值,而不是最大值。但最大池化的效果往往比这些替代方法更好。
简而言之,原因在于特征中往往编码了某种模式或概念在特征图的不同位置是否存在(因此得名特征图),而观察不同特征的最大值而不是平均值能够给出更多的信息。因此,最合理的子采样策略是首先生成密集的特征图(通过无步进的卷积),然后观察特征每个小图块上的最大激活,而不是查看输入的稀疏窗口(通过步进卷积)或对输入图块取平均,因为后两种方法可能导致错过或淡化特征是否存在的信息。
