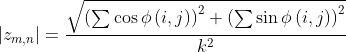相位解包裹（六）质量图导向法quality guide phase unwrapping（QGPU）

上一篇文章讲了通过连接残点形成branch的枝切法，这篇再介绍一种空间相位解包裹的算法，质量图导向法quality guide phase unwrapping（QGPU）。

 

质量图导向法QGPU

质量图导向法的核心是：通过一个优质的质量图，根据质量的大小，按质量从高到低的顺序来指导解包裹路径，从而躲开未被平衡的残点对解包裹的影响

可见，枝切法是先找残点，然后通过branch连接它们，解包裹的时候避开这些branch完成全图的相位解包裹。而QGPU则是先去计算一个质量图，根据质量图来解包裹。根据质量的大小来解包裹。总的来说，它们都是空间相位解包裹这一类下的算法，都是根据邻点的相位作为参考来解包裹，不过QGPU除了把残点留在最后去解包裹，在这之前的解包裹过程也是按照质量的大小去排列的，结果按理说会更优，但相对也会更耗时间。

 

质量图（quality map）

既然要用质量图来指导解包裹，那首先要知道质量图到底是什么东西。

按照Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software的定义，质量图就是用定义每个点的相位的质量或好坏的值的阵列（The arrays of values that define the quality or goodness of each pixel of the phase data）。

在书中，介绍了多种质量图的计算方法，分别是相关系数（Correlation coefficients）、伪相关系数（Pseudo-correlation coefficients）、相位差分方差（Phase derivative variance）、最大相位梯度（Maximum phase gradient）等等。

相关系数（Correlation coefficients）仅适用于IFSAR数据，所以这里不讨论。

 

伪相关系数（Pseudo-correlation coefficients）

在k*k邻域中计算第位置的伪相关系数，为k*k邻域的中心位置，是k*k邻域中各点的相位。

 

相位差分方差（Phase derivative variance）

在k*k邻域中计算第位置的相位差分方差，、分别是沿x轴方向和沿y轴方向的相位差，、分别是在k*k邻域中沿x轴方向和沿y轴方向的总的相位差的平均值。

 

最大相位梯度（Maximum phase gradient）

最大相位梯度一般为两个值的组合。

相位差分方差（Phase derivative variance）、最大相位梯度（Maximum phase gradient）都是描述相位的质量“劣”，而不是“优”，为了方便，所以都是取它们的相反数。

 

按书中介绍，最优的相关系数和相位差分方差，最大相位梯并不适应所有情况，伪相关系数在实际应用不是十分实用。

除此，在参考文献[4]还介绍了多种计算质量图的方式，主要是采用像傅里叶变换、窗口傅里叶变换、小波变换等来计算质量图。文章中还讨论了各种质量图的计算方法在不同情况下的优劣，有兴趣可以自己去下载来看看。我这里简单总结就是了。

质量图计算有两种情形，一种是从原始的测量数据中计算（case A），另一种是从截断相位图或归一化后的复数数据中计算（case B），针对A、B两种情况，对应的一些计算方式如下。

 文章中分析了质量图计算对噪声以及相位不连续的对比情况，简单总结就跳过了。

 

我用过的就是相位差分方差，和傅里叶变换提取基频，逆变换得到的复数矩阵中计算幅度谱，效果都差不多。一个合适的好的质量图，是后续相位解包裹正确完成的关键，所以具体情况还需要具体分析。

 

质量图导向法流程

以下为质量图导向法最基本的流程：

1、生成质量图

2、搜索质量图中，质量最大的位置作为起始点，将其四邻域的点解包裹，进队

3、只要队列非空，质量最高的点出队，将该点的四邻域、未进队且未被解包裹的点，解包裹，进队

4、重复步骤3，直到队列为空，相位图中所有点都已经被解包裹

如果仔细想想这个算法的实现，就会发现这个算法其实是相当耗时间的，因为随着进队的点越来越多，而每次都需要质量最大的点出队，相当于要做非常多次的质量大小比较，队列越长，比较的次数就越多，所需要的时间也会增加。

因此，需要算法的提速，需要考虑优化的数据结构来实现这个队列，参考文献[4]就有算法实现策略的对比，里面对比了多种数据结构实现的速度，参考文献[5]、参考文献[6]也提出了用不同的数据结构来实现QGPU。这里只讲算法基本原理，如何实现就不讲了，感兴趣可以自己看文章哦。

我个人用的是priority queue，也就是优先队列，由于我是用C++实现所有算法的，所以优先队列可以直接用C++ STL中的prority queue模板，当然也可以自己写最大堆的结构来实现。

 

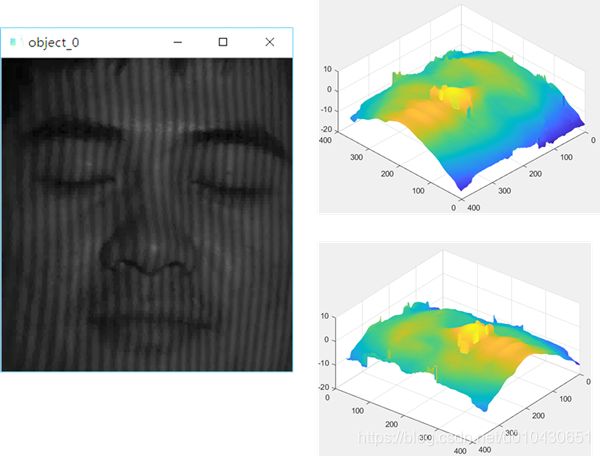
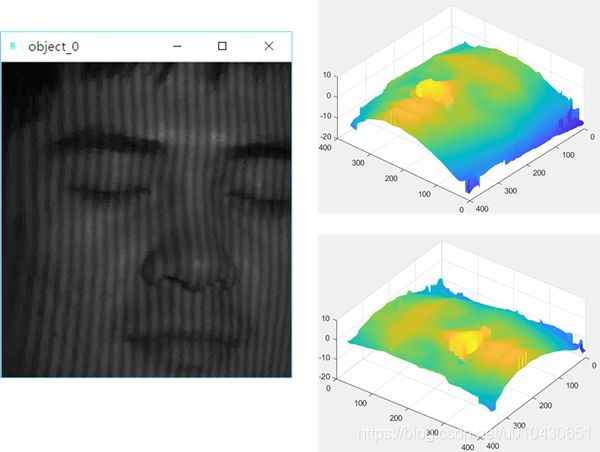
我在FTP文章里面放的人脸的重建，解包裹就是用QGPU来实现的，我感觉效果还算过得去吧，但也要考虑时间复杂度的问题。对于400*400的图，我写的算法解包裹平均要0.75s，电脑配置是i7-8750H CPU@ 2.20GHz, NVIDIA Geforce GTX1060, 16GB RAM，其实我对这个速度是相当不满意的，不过算法嘛，我也是个渣渣，也没想清楚怎么去提升速度，后来慢慢放弃了QGPU，去用时间相位解包裹的算法了（真香~）。

 

 

 

 

 

 

参考文献：

[1] Ghiglia D C, Pritt M D. Two-dimensional phase unwrapping: theory, algorithms, and software[M]. New York: Wiley, 1998.

[2] Xu W, Cumming I. A region-growing algorithm for InSAR phase unwrapping[J]. IEEE transactions on geoscience and remote sensing, 1999, 37(1): 124-134.

[3] Su X, Chen W. Reliability-guided phase unwrapping algorithm: a review[J]. Optics and Lasers in Engineering, 2004, 42(3): 245-261.

[4] Zhao M, Huang L, Zhang Q, et al. Quality-guided phase unwrapping technique: comparison of quality maps and guiding strategies[J]. Applied optics, 2011, 50(33): 6214-6224.

[5] Zhong H, Tang J, Zhang S, et al. An improved quality-guided phase-unwrapping algorithm based on priority queue[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 8(2): 364-368.

[6] Zhao M, Kemao Q. Quality-guided phase unwrapping implementation: an improved indexed interwoven linked list[J]. Applied optics, 2014, 53(16): 3492-3500.

 

声明：作者水平有限，如文中有错，请务必留言指正。如有学习交流需要，也可通过邮箱[email protected]联系我，大家一起讨论学习。