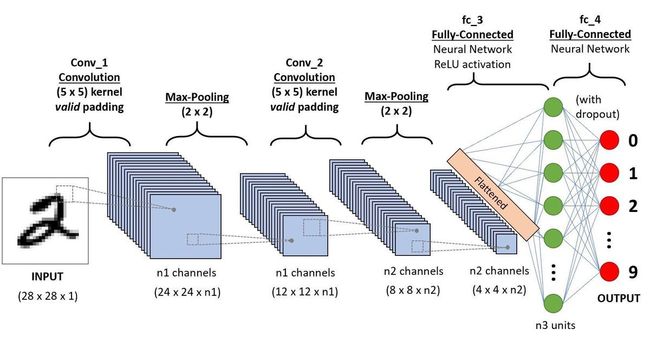
cnn卷积神经网络_Python 徒手实现 卷积神经网络 CNN

参考：CNNs, Part 1: An Introduction to Convolutional Neural Networks

参考：CNNs, Part 2: Training a Convolutional Neural Network

---

1. 动机（Motivation）

　　通过普通的神经网络可以实现，但是现在图片越来越大，如果通过 NN 来实现，训练的参数太多。例如 224 x 224 x 3 = 150,528，隐藏层设置为 1024 就需要训练参数 150,528 x 1024 = 1.5 亿 个，这还是第一层，因此会导致我们的网络很庞大。

　　另一个问题就是特征位置在不同的图片中会发生变化。例如小猫的脸在不同图片中可能位于左上角或者右下角，因此小猫的脸不会激活同一个神经元。

2. 数据集（Dataset）

　　我们使用手写数字数据集 MNIST 。

　　每个数据集都以一个 28x28 像素的数字。

　　普通的神经网络也可以处理这个数据集，因为图片较小，另外数字都集中在中间位置，但是现实世界中的图片分类问题可就没有这么简单了，这里只是抛砖引玉哈。

3. 卷积（Convolutions）

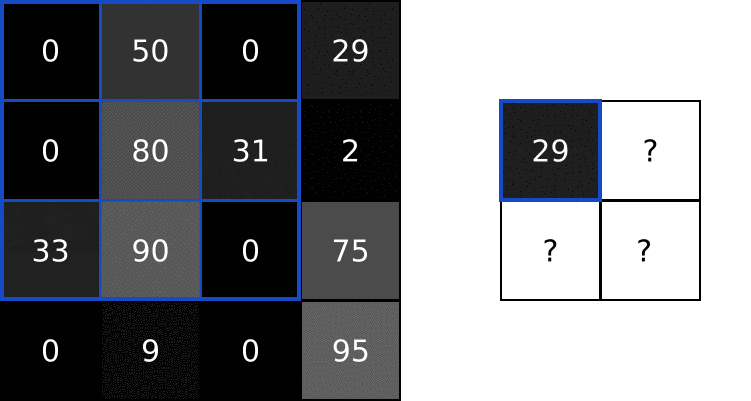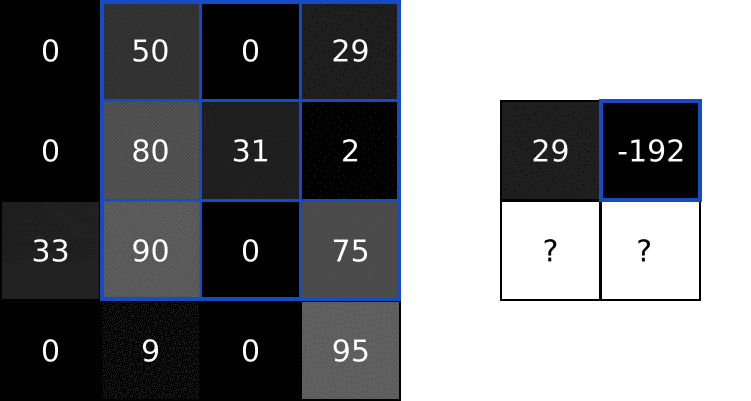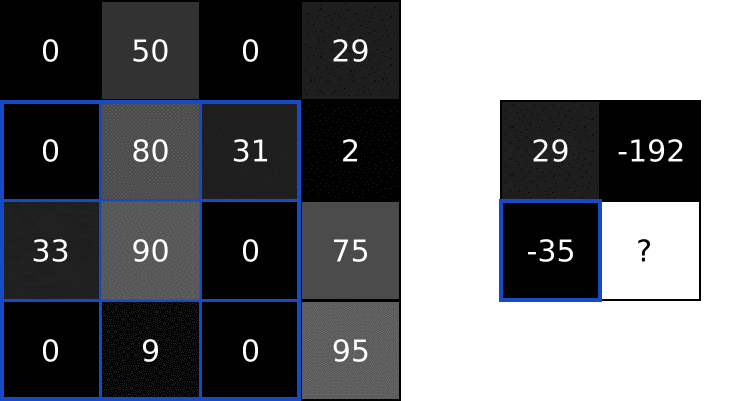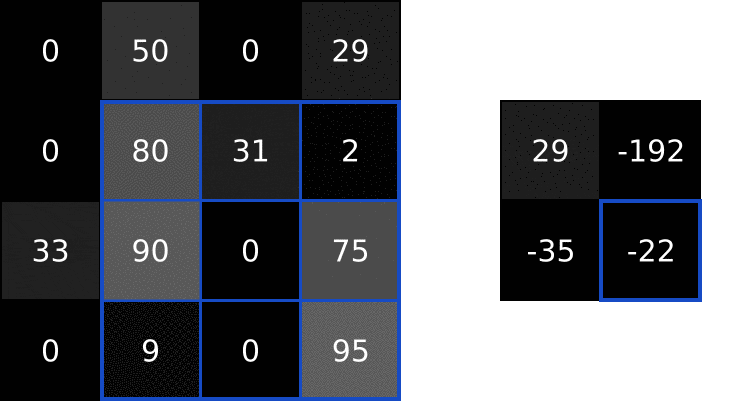
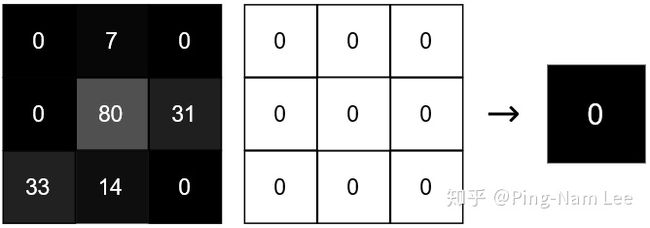
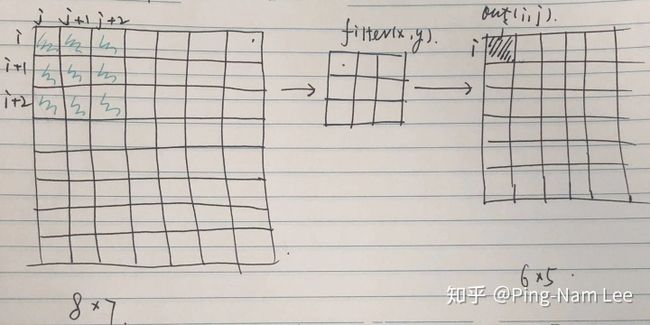
　　CNN 相较于 NN 来说主要是增加了基于 convolution 的卷积层。卷基层包含一组 filter，每一个 filter 都是一个 2 维的矩阵。以下为 3x3 filter：

　　我们可以通过输入的图片和上面的 filter 来做卷积运算，然后输出一个新的图片。包含以下步骤：

• • 将 filter 叠加在图片的顶部，一般是左上角
  • 然后执行对应元素的相乘
  • 将相乘的结果进行求和，得到输出图片的目标像素值
  • 重复以上操作在所有位置上

　　执行效果如下所示：

　　3.1 有用吗？

　　通过卷积可以提取图片中的特定线条，垂直线条或者水平线条，以下为 vertical Sobel filter and horizontal Sobel filter 的结果：

　　卷积可以帮助我们查找一些图片特征（例如边缘）。

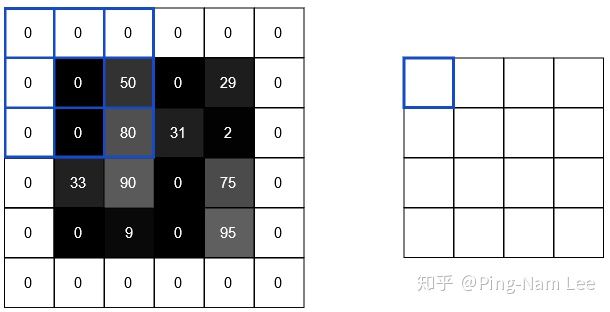
3.2 Padding（填充）

　　可以通过在周围补 0 实现输出前后图像大小一致，如下所示：

　　这叫做 "same padding"，不过一般不用 padding，叫做 "valid" padding。

3.3 卷基层

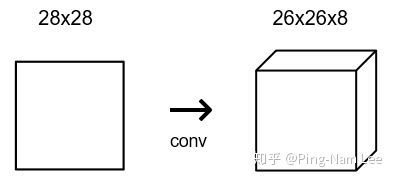
　　CNN 包含卷基层，卷基层通过一组 filter 将输入的图片转为输出的图片。卷基层的主要参数是 filter 的个数。

　　对于 MNIST CNN，我使用一个含有 8 个 filter 的卷基层，意味着它将 28x28 的输入图片转为 26x26x8 的输出集：

　　卷基层的 8 个 filter 分别产生 26x26 的输出，只有 3 x 3 (filter size) x 8 (nb_filters) = 72 权重值。

　　3.4 卷积层代码实现

　　简单起见，我们使用 3x3 的filter，首先实现一个 卷基层的类：

import 

　　Conv3x3 类只需要一个参数：filter 个数。通过 NumPy 的 randn() 方法实现。之所以在初始化的时候除以 9 是因为对于初始化的值不能太大也不能太小，参考：Xavier Initialization。

　　接下来，具体实现卷基层：

class 

4. 池化（Pooling） 　　

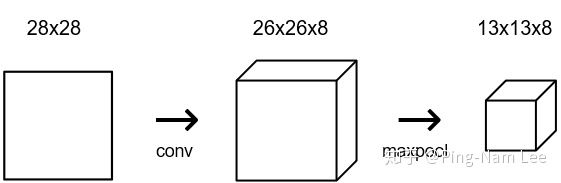
　　图片的相邻像素具有相似的值，因此卷基层中很多信息是冗余的。通过池化来减少这个影响，包含 max, min or average，下图为基于 2x2 的 Max Pooling：

　　与卷积计算类似，只是这个更容易，只是计算最大值并赋值。池化层将会把 26x26x8 的输入转为 13x13x8 的输出：

　　4.1 池化层代码实现

import numpy as np
 
class MaxPool2:
    # A Max Pooling layer using a pool size of 2.
 
    def iterate_regions(self, image):
        '''
        Generates non-overlapping 2x2 image regions to pool over.
        - image is a 2d numpy array
        '''
        # image: 26x26x8
        h, w, _ = image.shape
        new_h = h // 2
        new_w = w // 2
 
        for i in range(new_h):
            for j in range(new_w):
                im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]
                yield im_region, i, j
 
    def forward(self, input):
        '''
        Performs a forward pass of the maxpool layer using the given input.
        Returns a 3d numpy array with dimensions (h / 2, w / 2, num_filters).
        - input is a 3d numpy array with dimensions (h, w, num_filters)
        '''
        # input: 卷基层的输出，池化层的输入
        h, w, num_filters = input.shape
        output = np.zeros((h // 2, w // 2, num_filters))
 
        for im_region, i, j in self.iterate_regions(input):
            output[i, j] = np.amax(im_region, axis=(0, 1))
        return output

5. Softmax

　　为了完成我们的 CNN，我们需要进行具体的预测。通过 softmax 来实现，将一组数字转换为一组概率，总和为 1。参考：Softmax function。

　　5.1 用法

　　我们将要使用一个含有 10 个节点（分别代表相应数字）的 softmax 层，作为我们 CNN 的最后一层。最后一层为一个全连接层，只是激活函数为 softmax。经过 softmax 的变换，数字就是具有最高概率的节点。

　　softmax 为 13x13x8 转换为一列节点后与 10 个节点组成一个全连接，然后 softmax 为激活函数。

　　5.2 交叉熵损失函数（Cross-Entropy Loss）

　　交叉熵用来计算概率间的距离，具体公式可参考：笔记 | 什么是Cross Entropy。

　　其中：

• 为真实概率
• 为预测概率
• 为预测结果与真实结果的差距

　　在我们的具体问题中，对于真实概率，只有分类正确数字对应的概率为 1，其他均为 0，因此 交叉熵损失函数 可以写成如下形式：

　　其中，

是正确分类（本例中为正确的数字），

是

类的预测概率。

的值越小越好。

　　5.3 Softmax 层代码实现

import numpy as np
 
class Softmax:
    # A standard fully-connected layer with softmax activation.
 
    def __init__(self, input_len, nodes):
        # We divide by input_len to reduce the variance of our initial values
        # input_len: 输入层的节点个数，池化层输出拉平之后的
        # nodes: 输出层的节点个数，本例中为 10
        # 构建权重矩阵，初始化随机数，不能太大
        self.weights = np.random.randn(input_len, nodes) / input_len
        self.biases = np.zeros(nodes)
 
    def forward(self, input):
        '''
        Performs a forward pass of the softmax layer using the given input.
        Returns a 1d numpy array containing the respective probability values.
        - input can be any array with any dimensions.
        '''
        # 3d to 1d，用来构建全连接网络
        input = input.flatten()
 
        input_len, nodes = self.weights.shape
 
        # input: 13x13x8 = 1352
        # self.weights: (1352, 10)
        # 以上叉乘之后为 向量，1352个节点与对应的权重相乘再加上bias得到输出的节点
        # totals: 向量, 10
        totals = np.dot(input, self.weights) + self.biases
        # exp: 向量, 10
        exp = np.exp(totals)
        return exp / np.sum(exp, axis=0)

　　至此，我们完成了我们 CNN 模型的整个 forward pass！把它们放在一起调用：

import mnist
import numpy as np
 
# We only use the first 1k testing examples (out of 10k total)
# in the interest of time. Feel free to change this if you want.
test_images = mnist.test_images()[:1000]
test_labels = mnist.test_labels()[:1000]
 
conv = Conv3x3(8)                                    # 28x28x1 -> 26x26x8
pool = MaxPool2()                                    # 26x26x8 -> 13x13x8
softmax = Softmax(13 * 13 * 8, 10) # 13x13x8 -> 10
 
def forward(image, label):
    '''
    Completes a forward pass of the CNN and calculates the accuracy and
    cross-entropy loss.
    - image is a 2d numpy array
    - label is a digit
    '''
    # We transform the image from [0, 255] to [-0.5, 0.5] to make it easier
    # to work with. This is standard practice.
  
   # out 为卷基层的输出, 26x26x8
    out = conv.forward((image / 255) - 0.5)
    # out 为池化层的输出, 13x13x8
    out = pool.forward(out)
    # out 为 softmax 的输出, 10
    out = softmax.forward(out)
 
    # Calculate cross-entropy loss and accuracy. np.log() is the natural log.
    # 损失函数的计算只与 label 的数有关，相当于索引
    loss = -np.log(out[label])
    # 如果 softmax 输出的最大值就是 label 的值，表示正确，否则错误
    acc = 1 if np.argmax(out) == label else 0
 
    return out, loss, acc
 
print('MNIST CNN initialized!')
 
loss = 0
num_correct = 0
# enumerate 函数用来增加索引值
for i, (im, label) in enumerate(zip(test_images, test_labels)):
    # Do a forward pass.
    _, l, acc = forward(im, label)
    loss += l
    num_correct += acc
 
    # Print stats every 100 steps.
    if i % 100 == 99:
        print(
            '[Step %d] Past 100 steps: Average Loss %.3f | Accuracy: %d%%' %
            (i + 1, loss / 100, num_correct)
        )
        loss = 0
        num_correct = 0

　　输出结果如下所示：

MNIST CNN initialized!
[Step 100] Past 100 steps: Average Loss 2.302 | Accuracy: 11%
[Step 200] Past 100 steps: Average Loss 2.302 | Accuracy: 8%
[Step 300] Past 100 steps: Average Loss 2.302 | Accuracy: 3%
[Step 400] Past 100 steps: Average Loss 2.302 | Accuracy: 12%

　　这也比较合理，由于是通过随机的权重初始值，目前这个 CNN 模型跟我们随机猜测的结果类似。随机猜测的结果是 10%。

6. 训练概述（Training Overview）

　　训练神经网络一般包含两个阶段：

• forward phase: 输入参数传递通过整个网络。
• backward phase: 反向传播更新 gradient 和 weight。

　　我们按照如上的模式来训练 CNN。还有以下两个方法需要使用：

• 在 forward phase 中，每一层都需要存储一些数据（例如输入数据，中间值等）。这些数据将会在 backward phase 中得到使用。因此每一个 backward phase 都需要在相应的 forward phase 之后运行。
• 在 backward phase 中，每一层都要获取 gradient 并且也返回 gradient。获取的是 loss 对于该层输出（
  ）的 gradient，返回的是 loss 对于该层输入（
  ）的 gradient。

　　上面两个方法可以帮助我们更有条理且简洁的实现训练。训练 CNN 的代码大约长下面的样纸：

# Feed forward
 

7. 反向传播：Softmax（Backprop: Softmax）

　　我们需要从最后开始朝着最前面计算，这就是 backprop 的工作原理。首先回想下交叉熵损失函数（cross-entropy loss）：

　　其中，

是正确类

（也就是图片中的数字）的预测概率。

　　首先我们需要计算 softmax 层的 backward phase 的输入数据，

，其中

（下标的

是说明 softmax 层）是指 softmax 层的输出值：一个含有 10 个概率值的向量。由于

只出现在了 loss 方程中，因此很容易计算：

　　上面就是我们的初始化 gradient：

# Calculate initial gradient

　　现在我们已经准备好了开始实现我们第一个 backward phase，但是我们需要首先在 forward phase 中存储我们前面讨论的相关数据。

class 

　　接下来我们可以获取 backprop phase 的 gradient。 我们已经获取 softmax backward phase 的输入 gradient：

。由于只有一个是有值的，其他都是 0，因此我们可以忽略除了

之外的其他值！

　　首先，让我们计算

对于 totals （上面代码中的，softmax 转换前的值）的gradient。让

来表示 total 的类

。然后我们可以把

写作：

　　其中，

。

　　现在，开始考虑一些类

，其中

。我们可以把

写作：（由于只有

有值，因此只需考虑它就行了，其中

相当于常数不用考虑）

　　使用 Chain Rule 得到：

　　上面是针对

。现在让我们算下

的时候，如下所示：

　　合并如下：

　　如下实现：

class Softmax:
    # ...
 
    def backprop(self, d_L_d_out):
        '''
        Performs a backward pass of the softmax layer.
        Returns the loss gradient for this layer's inputs.
        - d_L_d_out is the loss gradient for this layer's outputs.
        '''
        # We know only 1 element of d_L_d_out will be nonzero
        for i, gradient in enumerate(d_L_d_out):
            # 找到 label 的值，就是 gradient 不为 0 的
            if gradient == 0:
                continue
 
            # e^totals
            t_exp = np.exp(self.last_totals)
 
            # Sum of all e^totals
            S = np.sum(t_exp)
 
            # Gradients of out[i] against totals
            # 初始化都设置为 非 c 的值，再单独修改 c 的值
            d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
            d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
 
            # ... to be continued

　　 我们继续哈。我们最终是想要计算 loss 对于 weights，biases 和 input 的 gradient：

• 我们要使用 weights gradient，
  ，来更新层的 weights。
• 我们要使用 biases gradient，
  ，来更新层的 biases。
• 我们要返回 input（每一层的正向输入） 的 gradient，
  ，基于 backprop 的方法，所以下一层可以使用它。

　　为了计算上面 3 个 loss gradient，我们首先需要获取另外 3 个结果：totals（做 softmax 之前的向量，10 个元素）对于 weights，biases 和 input 的 gradient。相关公式如下：（以下为对于单独 weight 的计算，但是代码实现的时候是通过 matrix，相对抽象）

　　这些 gradient 很容易计算：

　　根据 Chain Rule 把它们放在一起：

　　其中，

• ：loss 函数
• ：做 softmax 的输出结果，与 loss 公式直接相关的 概率
• ：做 softmax 的输入参数，通过 weights，bias 以及 softmax 层的输入来获取

　　把它们一并放到代码中实现如下：

class Softmax:
    # ...
 
    def backprop(self, d_L_d_out):
        '''
        Performs a backward pass of the softmax layer.
        Returns the loss gradient for this layer's inputs.
        - d_L_d_out is the loss gradient for this layer's outputs.
        '''
        # We know only 1 element of d_L_d_out will be nonzero
        for i, gradient in enumerate(d_L_d_out):
            if gradient == 0:
                continue
 
            # e^totals
            t_exp = np.exp(self.last_totals)
 
            # Sum of all e^totals
            S = np.sum(t_exp)
 
            # Gradients of out[i] against totals
            d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
            d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
 
            # NEW ADD
            # Gradients of totals against weights/biases/input
            # d_t_d_w 的结果是 softmax 层的输入数据，1352 个元素的向量
            # 不是最终的结果，最终结果是 2d 矩阵，1352x10
            d_t_d_w = self.last_input
            d_t_d_b = 1
            # d_t_d_input 的结果是 weights 值，2d 矩阵，1352x10
            d_t_d_inputs = self.weights
 
            # Gradients of loss against totals
            # 向量，10
            d_L_d_t = gradient * d_out_d_t
 
            # Gradients of loss against weights/biases/input
            # np.newaxis 可以帮助一维向量变成二维矩阵
            # (1352, 1) @ (1, 10) to (1352, 10)
            d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
            d_L_d_b = d_L_d_t * d_t_d_b
            # (1352, 10) @ (10, 1) to (1352, 1)
            d_L_d_inputs = d_t_d_inputs @ d_L_d_t
            # ... to be continued

　　 计算出 gradient 之后，剩下的就是训练 softmax 层。我们通过 SGD（Stochastic Gradient Decent）来更新 weights 和 bias，并返回 d_L_d_inputs：

class Softmax
    # ...
 
    # ADD A NEW PARAMETER - learn_rate
    def backprop(self, d_L_d_out, learn_rate):
        '''
        Performs a backward pass of the softmax layer.
        Returns the loss gradient for this layer's inputs.
        - d_L_d_out is the loss gradient for this layer's outputs.
        - learn_rate is a float
        '''
        # We know only 1 element of d_L_d_out will be nonzero
        for i, gradient in enumerate(d_L_d_out):
            if gradient == 0:
                continue
 
            # e^totals
            t_exp = np.exp(self.last_totals)
 
            # Sum of all e^totals
            S = np.sum(t_exp)
 
            # Gradients of out[i] against totals
            d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
            d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
 
            # Gradients of totals against weights/biases/input
            d_t_d_w = self.last_input
            d_t_d_b = 1
            d_t_d_inputs = self.weights
 
            # Gradients of loss against totals
            d_L_d_t = gradient * d_out_d_t
 
            # Gradients of loss against weights/biases/input
            d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
            d_L_d_b = d_L_d_t * d_t_d_b
            d_L_d_inputs = d_t_d_inputs @ d_L_d_t
 
            # NEW ADD
            # Update weights / biases
            self.weights -= learn_rate * d_L_d_w
            self.biases -= learn_rate * d_L_d_b
            # 将矩阵从 1d 转为 3d
            # 1352 to 13x13x8
            return d_L_d_inputs.reshape(self.last_input_shape)

　　注意我们添加了 learn_rate 参数用来控制更新 weights 与 biases 的快慢。此外，我们需要将 d_L_d_inputs 进行 reshape() 操作，因为我们在 forward pass 中将 input 进行了 flatten() 操作。reshape() 操作之后，保证与原始输入具有相同的结构。

8. 反向传播：池化层（Backprop: Max Pooling）

　　池化层不需要训练，因为它里面不存在任何 weights，但是为了计算 gradient 我们仍然需要实现一个 backprop() 方法。首先我们还是需要存储一些临时数据在 forward phase 里面。我们这次需要存储的是 input。

class MaxPool2:
    # ...
 
    def forward(self, input):
        '''
        Performs a forward pass of the maxpool layer using the given input.
        Returns a 3d numpy array with dimensions (h / 2, w / 2, num_filters).
        - input is a 3d numpy array with dimensions (h, w, num_filters)
        '''
        # 存储 池化层 的输入参数，26x26x8
        self.last_input = input
        # More implementation
        # ...

　　在 forward pass 的过程中，Max Pooling 层选取 2x2 块的最大值进行输入，如下图所示：

　　backward phase 中的相同层如下图所示：

　　每一个 gradient 的值都被赋值到原始的最大值的位置，其他的值都是 0。

　　为什么 backward phase 的 Max Pooling 层显示如上呢？让我们直觉思考下

（Max Pooling 的输入数据，26x26x8）的值是多少。对于 2x2 数据块中不是最大值的输入像素将不会对 loss 产生任何影响，因为稍微改变这个值并不会改变输出！换句话说，对于非最大值的像素点：

。另一方面，最大值的像素点会将值传递给输出，所以

，也就是说，

。

　　总结后就是：（output 与 input 都是相对于 Max Pooling 层来说的）

　　代码实现如下：

class MaxPool2:
    # ...
 
    def iterate_regions(self, image):
        '''
        Generates non-overlapping 2x2 image regions to pool over.
        - image is a 2d numpy array
        '''
        h, w, _ = image.shape
        new_h = h // 2
        new_w = w // 2
 
        for i in range(new_h):
            for j in range(new_w):
                im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]
                yield im_region, i, j
 
    def backprop(self, d_L_d_out):
        '''
        Performs a backward pass of the maxpool layer.
        Returns the loss gradient for this layer's inputs.
        - d_L_d_out is the loss gradient for this layer's outputs.
        '''
        # 池化层输入数据，26x26x8，默认初始化为 0
        d_L_d_input = np.zeros(self.last_input.shape)
 
        # 每一个 im_region 都是一个 3x3x8 的8层小矩阵
        # 修改 max 的部分，首先查找 max
        for im_region, i, j in self.iterate_regions(self.last_input):
            h, w, f = im_region.shape
            # 获取 im_region 里面最大值的索引向量，一叠的感觉
            amax = np.amax(im_region, axis=(0, 1))
 
            # 遍历整个 im_region，对于传递下去的像素点，修改 gradient 为 loss 对 output 的gradient
            for i2 in range(h):
                for j2 in range(w):
                    for f2 in range(f):
                        # If this pixel was the max value, copy the gradient to it.
                        if im_region[i2, j2, f2] == amax[f2]:
                            d_L_d_input[i * 2 + i2, j * 2 + j2, f2] = d_L_d_out[i, j, f2]
 
        return d_L_d_input

　　对于每一个 2x2 的像素块，我们找到 forward pass 中最大值的像素点，然后将 loss 对 output 的 gradient 复制过去 。

　　就是酱紫来弄，接下来是最后一层了。

9. 反向传播：卷积层（Backprop: Conv）

　　终于到卷基层了：卷积层的反向传播是 CNN 模型训练的核心。forward phase 存储很简单：

class Conv3x3
    # ...
 
    def forward(self, input):
        '''
        Performs a forward pass of the conv layer using the given input.
        Returns a 3d numpy array with dimensions (h, w, num_filters).
        - input is a 2d numpy array
        '''
        # 输入大数据，28x28
        self.last_input = input
        # More implementation
        # ...

　　我们主要是对卷基层的 filter 感兴趣，因为我们需要跟新 filter 的 weight。我们已经得到了卷积层的

，所以我们需要获取

。为了计算这个值，我们需要问下自己：怎么样改变 filter 的 weight 来影响 卷积层 的输出的？

　　实际上，改变任何 filter 的 weight 都会影响到整个输出图片的信息，因为在卷积过程中，每一个输出的像素都会使用每一个 filter 的 weight。为了简单起见，我们试想下一次只有一个输出：如何修改 filter 来改变那个具体输出像素的值？

　　下面这个例子有助于我们思考这个问题：

　　我们有一个 3x3 的图片与一个都是 0 的 3x3 的 filter 进行卷积运算，结果只有一个 1x1 的输出。如果我们把 filter 中间的 weight 增加到 1 呢？输出将会随着中心值来增加到 80：

　　简单起见，增加任何 filter 的其他权重到 1，都会最终增加相应的输出图片像素值！这说明一个具体的输出像素对于具体的 filter 的 weight 的 gradient 就是对应的像素值。推导如下：

　　如下图所示，对于任意一个

都是通过 image 中的 3x3 矩阵 与 filter 的 3x3 矩阵进行点乘求和获取的，因此对于 任意一个

对于 任意一个

的 gradient 就是与其对应相乘的那个像素点

。

　　于是，我们可以实现卷积层的 backprop 如下：

class Conv3x3
    # ...
 
    def backprop(self, d_L_d_out, learn_rate):
        '''
        Performs a backward pass of the conv layer.
        - d_L_d_out is the loss gradient for this layer's outputs.
        - learn_rate is a float.
        '''
        # 初始化一组为 0 的 gradient，3x3x8
        d_L_d_filters = np.zeros(self.filters.shape)
 
        # im_region，一个个 3x3 小矩阵
        for im_region, i, j in self.iterate_regions(self.last_input):
            for f in range(self.num_filters):
                # 按 f 分层计算，一次算一层，然后累加起来
                # d_L_d_filters[f]: 3x3 matrix
                # d_L_d_out[i, j, f]: num
                # im_region: 3x3 matrix in image
                d_L_d_filters[f] += d_L_d_out[i, j, f] * im_region
 
        # Update filters
        self.filters -= learn_rate * d_L_d_filters
 
        # We aren't returning anything here since we use Conv3x3 as
        # the first layer in our CNN. Otherwise, we'd need to return
        # the loss gradient for this layer's inputs, just like every
        # other layer in our CNN.
        return None

　　至此，我们已经实现了 CNN 的整个 backward pass。接下来我们来测试下...

　　完整代码参考：CNN from scratch - github

10. 训练 CNN（Training a CNN）

　　我们将要训练我们的 CNN 模型通过几个 epoch，跟踪训练中的改进，并且在另外的测试集上进行测试。下面是完整的代码：

import 

　　例子的输出结果如下：

MNIST CNN initialized!
--- Epoch 1 ---
[Step 100] Past 100 steps: Average Loss 2.254 | Accuracy: 18%
[Step 200] Past 100 steps: Average Loss 2.167 | Accuracy: 30%
[Step 300] Past 100 steps: Average Loss 1.676 | Accuracy: 52%
[Step 400] Past 100 steps: Average Loss 1.212 | Accuracy: 63%
[Step 500] Past 100 steps: Average Loss 0.949 | Accuracy: 72%
[Step 600] Past 100 steps: Average Loss 0.848 | Accuracy: 74%
[Step 700] Past 100 steps: Average Loss 0.954 | Accuracy: 68%
[Step 800] Past 100 steps: Average Loss 0.671 | Accuracy: 81%
[Step 900] Past 100 steps: Average Loss 0.923 | Accuracy: 67%
[Step 1000] Past 100 steps: Average Loss 0.571 | Accuracy: 83%
--- Epoch 2 ---
[Step 100] Past 100 steps: Average Loss 0.447 | Accuracy: 89%
[Step 200] Past 100 steps: Average Loss 0.401 | Accuracy: 86%
[Step 300] Past 100 steps: Average Loss 0.608 | Accuracy: 81%
[Step 400] Past 100 steps: Average Loss 0.511 | Accuracy: 83%
[Step 500] Past 100 steps: Average Loss 0.584 | Accuracy: 89%
[Step 600] Past 100 steps: Average Loss 0.782 | Accuracy: 72%
[Step 700] Past 100 steps: Average Loss 0.397 | Accuracy: 84%
[Step 800] Past 100 steps: Average Loss 0.560 | Accuracy: 80%
[Step 900] Past 100 steps: Average Loss 0.356 | Accuracy: 92%
[Step 1000] Past 100 steps: Average Loss 0.576 | Accuracy: 85%
--- Epoch 3 ---
[Step 100] Past 100 steps: Average Loss 0.367 | Accuracy: 89%
[Step 200] Past 100 steps: Average Loss 0.370 | Accuracy: 89%
[Step 300] Past 100 steps: Average Loss 0.464 | Accuracy: 84%
[Step 400] Past 100 steps: Average Loss 0.254 | Accuracy: 95%
[Step 500] Past 100 steps: Average Loss 0.366 | Accuracy: 89%
[Step 600] Past 100 steps: Average Loss 0.493 | Accuracy: 89%
[Step 700] Past 100 steps: Average Loss 0.390 | Accuracy: 91%
[Step 800] Past 100 steps: Average Loss 0.459 | Accuracy: 87%
[Step 900] Past 100 steps: Average Loss 0.316 | Accuracy: 92%
[Step 1000] Past 100 steps: Average Loss 0.460 | Accuracy: 87%
 
--- Testing the CNN ---
Test Loss: 0.5979384893783474
Test Accuracy: 0.78

　　我们的代码效果不错，实现了 78% 的准确率。

11. Keras 实现

　　通过 Keras 实现上面的功能如下：

import 

　　以上代码应用了 MNIST 的全部数据集，结果如下：

Epoch 1
loss: 0.2433 - acc: 0.9276 - val_loss: 0.1176 - val_acc: 0.9634
Epoch 2
loss: 0.1184 - acc: 0.9648 - val_loss: 0.0936 - val_acc: 0.9721
Epoch 3
loss: 0.0930 - acc: 0.9721 - val_loss: 0.0778 - val_acc: 0.9744

　　得到 97.4% 的准确率！