【车间调度】柔性作业车间调度问题的研究方法

本系列为自己学习调度相关知识的记录，如有误请指出，也欢迎调度方向的小伙伴加我好友共同交流。

从Johnson揭开调度问题研究的序幕以来，调度问题一直是极其困难的组合优化问题，调度模型从简单到复杂，研究方法也随着调度模型的变迁从开始的数学方法到启发式的智能算法。目前解决调度问题的方法主要分为两类：精确方法（exact method）和近似方法（approximation method）。精确方法也可称为最优化方法，能够保证得到全局最优解，但只能解决较小规模的问题，而且速度很慢。近似方法求解时，可以很快地得到问题的解，但不能保证得到的解是最优的，不过对于大规模问题是非常合适的，可以较好地满足实际问题的需求。下图为近年来求解调度问题的主要研究方法。

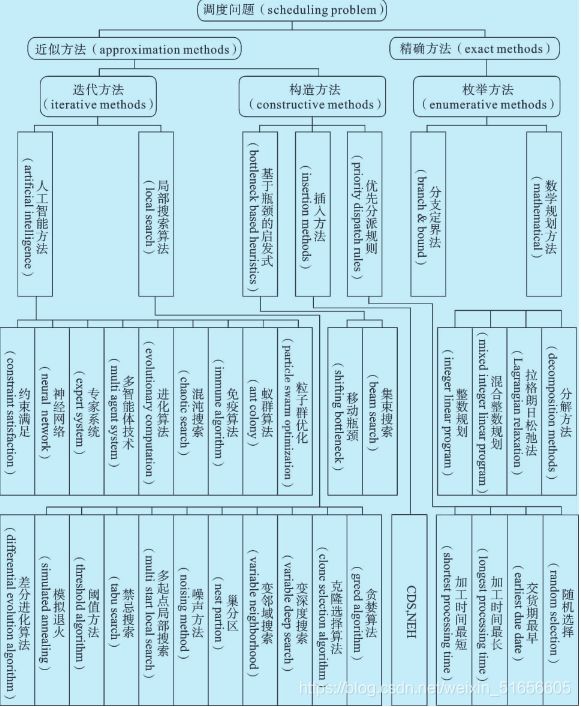
精确方法

精确方法主要包括整数规划、混合整数规划、拉格朗日松弛法、分解方法及分支定界法等。

1.数学规划方法

数学规划方法中求解调度问题的最常见方法是混合整数规划。混合整数规划有一组线性约束和一个线性目标函数，该方法限制决策变量都必须是整数。导致在运算中出现的整数个数以指数规模增长，即便使用更好更简洁的公式表述，也需要大量的约束条件。较多成功的数学模型的建立都归功于拉格朗日松弛法（Lagrangian relaxation）和分解方法（decomposition method）。拉格朗日松弛法用非负拉格朗日乘子将工艺约束和资源约束进行松弛，最后将惩罚函数加入目标函数中。上海交通大学的刘学英用拉格朗日松弛法解决车间调度问题。分解方法将原问题分解为多个小的易于解决的子问题，然后对子问题寻找最优。

2.分支定界法

分支定界法（branch&bound，Ｂ＆Ｂ）用动态树结构来描述所有的可行解排序的解空间，树干的分支隐含有要被搜索的可行解。Balas在1969年提出基于析取图的枚举算法是最早应用于调度问题求解的Ｂ＆Ｂ方法。Ｂ＆Ｂ非常适合解决总工序数小于250的问题，对于大规模的调度问题，它需要很多的计算时间，限制了它的使用。目前，对这种方法研究的重心是如何与智能算法相结合，减少最初的搜索阶段中的节点，提高搜索效率和求解效果。

近似方法

1.构造方法

构造方法主要包括优先分派规则法、插入方法和基于瓶颈的启发式方法等。

1.1 优先分派规则法

优先分派规则法（priority dispatch rules,PDR）是最早的近似方法。该方法给所有的被加工工序分派一个优先权，然后优先权最高的加工工序被最先选出排序，接下来按优先权次序依次进行排序。该方法非常容易实现，而且计算复杂性低，在实际的调度问题中常常被使用。Panwalkar和Iskander对各种不同规则进行了归纳和总结。在实际中常用的规则有SPT、LPT、EDD、MOR和FCFS等。大量该领域的研究表明：对于大规模的车间调度问题，多种优先分派规则组合起来使用更具有优势；另外，该方法具有短视的缺点，如它只考虑机器的当前状态和解的质量等级等问题。

1.2 基于瓶颈的启发式方法

一般而言，基于瓶颈的启发式方法（bottleneck based heuristic BBH）主要包括瓶颈移动方法（shifting bottleneck procedure ,SBP）和射束搜索方法。SBPP是目前求解调度问题最有效的构造方法之一，由Adams在1988年提出，也是第一个解决FT10标准测试实例的启发式算法。SBP的主要贡献是：提供了一种用单一机器确定将要排序的机器的排序途径。用SBP实际求解时，把问题化为多个单一机器问题，每次解决一个子问题，把每个子问题的解与所有其他子问题的解比较，每个机器依解的好坏排列，有着最大下界的机器被认为是瓶颈机器。而单一机器问题的排序用Carlier的方法通过迭代来解决，这个方法可以快速给出一个精确的解。当每次瓶颈机器排序后，每个先前被排定的有改进能力的机器，通过解决单一机器问题的方法，再次被局部重新最优化。虽然SBP可以得到比优先分派规则法质量更好的解，但是计算时间较长，而且实现比较复杂。

2.人工智能方法

主要包括：约束满足技术、神经网络、专家系统、多智能体技术，以及后来人们通过模拟或揭示某些自然现象、过程和规律而发展的元启发式算法（如遗传算法、免疫算法、蚁群优化算法和粒子群优化算法等）。

2.1 约束满足

约束满足（constraint satisfaction,CS）是指通过运用约束来减少搜索空间的有效规模的方法。这些约束限制了选择变量的次序和分配到每个变量可能值的排序，在一个值被分配给一个变量后，不一致的情况被剔除。去掉不一致的过程称为一致性检查（consistency checking），但是这需要进行回访修正。当所有的变量都得到分配的值，并且不与约束条件冲突时，约束满足问题就得到了解决。Pesch和Tetzlaff指出，该方法只是在一定程度上给调度者高水平的指导方针，较少应用于实际调度。

2.2 神经网络

神经网络（neural networks ,NN）通过一个Lyaplmov能量函数来构造网络的极值，当网络迭代收敛时，能量函数达到极小，使与能量函数对应的目标函数得到优化。用ＮＮ解决旅行商问题（TSP）是其在组合优化问题中最成功的应用之一。Foo和Takefuji最早提出用Hopfield模型求解车间调度问题。之后大量研究人员进行了改进性研究。除了Hopfield模型之外，ＢＰ（back propagation）模型也较多地应用于求解车间调度问题。Remus最早利用ＢＰ模型求解调度问题，之后大量研究人员对此模型进行研究。目前，神经网络仅能解决规模较小的调度问题，而且计算效率非常低，以至于不能较好地用于求解实际大规模的调度问题。

2.3 专家系统

专家系统（expert system，ES）是指一种能够在特定领域内模拟人类专家思维来解决复杂问题的计算机程序。专家系统通常由人机交互界面、知识库、推理机、解释器、综合数据库和知识获取等六个部分构成。它将传统的调度方法与基于知识的调度评价相结合，根据给定的优化目标和系统当前状态，对知识库进行有效的启发式搜索和并行模糊推理，避开烦琐的计算，选择最优的调度方案，为在线决策提供支持。比较著名的专家系统有：ISIS,OPIS,CORTES,SOJA等。由于专家系统需要丰富的调度经验和大量知识的积累，使得开发周期较长，成本昂贵，对新环境的适应能力较差，因此专家系统一般对领域的要求非常严格，非常特定。

2.4 多智能体技术

为了解决复杂问题，克服由于单一的专家系统所造成的知识有限、处理能力弱等问题，出现了分布式人工智能（distributed artificial intelligence,DAI）。多个智能体的协作正好符合分布式人工智能的要求，因此出现了多智能体系统（multi-agent system,MAS）。由于ＭＡＳ对开放和动态的实际生产环境具有良好的灵活性和适应性，因此MAS在实际生产中不确定因素较多的车间调度等领域中获得越来越多的应用。不过，MAS和专家系统具有相同的不足：需要丰富的调度经验和大量知识的积累等

2.5 进化算法

进化算法（evolutionary algorithm EA）通常包括遗传算法（genetic algorithm GA）、遗传规划（genetic programming,GP）、进化策略（evolution strategies ES）和进化规划（evolutionary programming EP）。它们都是模仿生物遗传和自然选择的机理，用人工方式构造的一类优化搜索算法。侧重点不一样，ＧＡ主要发展自适应系统，是应用最广的算法；ＥＰ主要求解预期问题；ＥＳ主要解决参数优化问题。１９８５年，Davis最早将ＧＡ应用到调度问题，通过一个简单的２０×６的车间调度问题验证了采用ＧＡ的可行性。此后，Falkenauer和Bouffouix进一步改进提高。1991年，Nakano首先将ＧＡ应用到了一系列的JSP的典型问题中。Yamada和Nakano在1992年提出了一种基于Giffler和Thompson的算法ＧＡ／ＧＴ。自Holland教授1975年提出ＧＡ以来，国内对其在求解车间调度问题的文献非常多，其中清华大学的王凌和郑大钟较好地对ＧＡ及其在调度问题中的应用进行了分析和总结

2.6 蚁群优化算法

蚁群优化算法（ant colony optimization ACO）是意大利学者Dorigo等于1991年提出的，模拟蚂蚁在寻找食物过程中发现路径的行为。蚂蚁在寻找食物过程中，会在它们经过的地方留下一些化学物质“外激素（stigmergy）”或“信息素（pheromone）”，这些物质能被同一蚁群中后来的蚂蚁感受到，并作为一种信号影响后来者的行动，而后来者也会留下外激素对原有的外激素进行修正，如此反复循环下去，外激素最强的地方形成一条路径。Colorin等首先将蚁群优化算法求解车间调度问题，国内也有许多学者进行此方面研究。蚁群优化算法在求解复杂组合优化方面有一定的优越性，不过容易出现停滞现象，收敛速度慢。

2.7 粒子群优化算法

粒子群优化（particle swarm optimization PSO）算法由Eberhart博士和Kennedy博士在１９９５年提出，源于对鸟群捕食行为的模拟研究。在PSO算法中，系统初始化为一组随机解，称为粒子。每个粒子都有一个适应值表示粒子的位置，还有一个速度来决定粒子飞行的方向和距离。在每一次迭代中，粒子通过两个极值来更新自己：一个极值是粒子自身所找到的最优解，称为个体极值；另一个极值是整个种群目前找到的最优解，称为全局极值。PSO算法在车间调度中的应用国内研究较多，作者在PSO算法应用方面做了大量工作。PSO算法最初应用于连续问题优化，如何较好的离散化应用于组合优化问题是一个研究热点.

3.局部搜索算法

局部搜索（local search,LS）是人们从生物进化、物理过程中受到启发用于求解组合优化问题的方法，是从早期的启发式算法变化而来的。以模拟退火、禁忌搜索为代表，应用广泛。局部搜索必须依据问题设计优良的邻域结构，产生较好的邻域解来提高算法的搜索效率和能力。

4.1 模拟退火

模拟退火（simulated annealing ，ＳＡ）是Kirtpatrick等在1983年提出的，源于模拟退火的过程并且结合Metropolis准则。模拟退火算法在进行局部搜索过程中，当某个解的目标函数值即使变坏时，仍可以采用Metropolis准则以一定的概率接受新的较差解或继续在当前邻域内搜索，以免陷入局部最优解，整个过程由一个称为温度的参数ｔ来控制。Laarhoven和Matsuo在1988年首先将ＳＡ算法用于求解车间调度问题。此后Laarhoven对ＳＡ算法进行改进，取得了较好的求解结果。由于SA算法是一般的随机搜索算法，搜索过程没有记忆功能，求解调度问题时不能非常迅速地得到较好解。不过，SA算法与其他算法相结合可以增强局部搜索能力，可以在结果和计算时间上都有明显改善

4.2 禁忌搜索

禁忌搜索（tabu search，ＴＳ）由Golver和Hansen在1986年提出。TS在运行时，按照某种方式产生一个初始解，然后搜索其邻域内的所有可行解，取其最优解作为当前解。为了避免重复搜索，引入了灵活的存储结构和相应的禁忌准则（即禁忌表和禁忌对象）；为了避免陷入局部最优，而引入特赦准则，允许一定程度地接受较差解。1996年，Nowicki和Smutnicki设计了一种基于关键路径的邻域结构，对用TS算法求解调度问题影响非常大。TS算法求解速度快而且应用较为广泛，然而它依赖于问题模型和邻域结构等，可以与其他算法结合提高局部搜索能力。

除了上述方法以外，还有很多种方法对调度问题进行求解，如Petri网和仿真调度法、文化算法（cultural algorithm,）、DNA算法、Memetic算法、分散搜索（scatter search）等。每一种算法都有一定的优势，却也存在一定的缺点，如何将它们取长补短的混合在一起进行使用是当前及未来研究的热点.