python数据结构和算法【总结】
一。什么是算法
算法是计算机处理信息的本质,因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务。一般地,当算法在处理信息时,会从输入设备或数据的存储地址读取数据,把结果写入输出设备或某个存储地址供以后再调用。
通俗的来讲,算法就是你解决问题的思路。
二。算法的五大特性
- 输入: 算法具有0个或多个输入
- 输出: 算法至少有1个或多个输出
- 有穷性: 算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成
- 确定性:算法中的每一步都有确定的含义,不会出现二义性
- 可行性:算法的每一步都是可行的,也就是说每一步都能够执行有限的次数完成
三。时间复杂度
我们可以通过算法的执行来判断算法的优劣。但这个执行时间本身又收到程序执行环境(硬件)的影响。有没有什么可以客观的衡量算法的优劣呢? ----------时间复杂度
我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位,那么有多少个基本操作就代表会花费多少时间单位。
每台机器执行的总时间不同,但同一算法执行的步骤数量在每台机器上是相同的。
时间复杂度可以用步骤的数量来表示,从而来表示算法的优劣
在计算时间复杂度时注意: N 问题的规模 走势的影响 数量级
- 算法的速度并非指时间,不是以秒为单位;而是操作数的增速。从增量的角度度量的。
- 平时说的算法的速度,指的是随着输入的增加,其运行时间将会以什么样的速度进行增加。
---------------------------------------------------------------------------------------------------
“大O记法”:对于单调的整数函数f,如果存在一个整数函数g和实常数c>0,使得对于充分大的n总有f(n)<=c*g(n),就说函数g是f的一个渐近函数(忽略常数),记为f(n)=O(g(n))。也就是说,在趋向无穷的极限意义下,函数f的增长速度受到函数g的约束,亦即函数f与函数g的特征相似。
时间复杂度:假设存在函数g,使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n)),则称O(g(n))为算法A的渐近时间复杂度,简称时间复杂度,记为T(n)
---------------------------------------------------------------------------------------------------------
- 时间复杂度的计算
1.基本操作, 基本步骤,(一行语句)随着n的增大,不受影响。即只有常数项,认为其时间复杂度为O(1)
2.顺序结构,时间复杂度按假发进行计算
3.循环结构,时间复杂度按乘法进行计算
4.分支结构,时间复杂度取最大值
5.判断一个算法的效率,往往只需要关注操作数量的最高次项 ,其他次要项和常数项可以忽略
6.在没有特殊说明时,我们所分析的算法的时间复杂度都是值最坏时间复杂度
常见时间复杂度
|
执行次数函数举例 |
阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n2+2n+1 | O(n2) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n3+2n2+3n+4 | O(n3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
四。数据结构
一个学生的信息可以通过list存储,也可以用字典dict的方式存储。在这两种的存储放下下查找学生的信息时,时间复杂度时不相同的。
我们为了解决问题,需要将数据保存下来,然后根据数据的存储方式来设计算法实现进行处理,那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好,于是我们就需要考虑数据究竟如何保存的问题,这就是数据结构。
所以算法和数据结构是不可分割的
数据是一个抽象的概念,将其进行分类后得到程序设计语言中的基本类型。如:int float char 等。而计算机能正真存储在物理单元中和使用的也只有基本的数据类型。数据元素之间不是独立的,存在特定的关系,这些关系便是结构。比如,python中的list,他是由基本的数据类型组成,表达的是这些数据之间一定的关系。
python给我们提供了很多现成的数据结构,这些系统自己定义好的,不需要我们自己去定义的数据结构叫做python的内置数据结构,比如列表,元组,字典。而有些数据组织方式,python系统里面没有直接定义,需要我们自己去定义实现这些数据的组织方式,这些数据组织方式称之为python的扩展数据结构,比如栈,队列等。
五。算法与数据结构的区别
将基本的数据类型利用一定的关系组织到一起,就是我们所说的数据结构。
数据结构只是静态的描述了数据元素之间的关系。
高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法
总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
六。抽象数据类型(Abstract Data Type)
数学模型(数据结构)+数学模型上的一组操作,操作的具体实现无需定义
抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起,进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开,使它们相互独立。
最常用的数据运算有五种:
- 插入
- 删除
- 修改
- 查找
- 排序
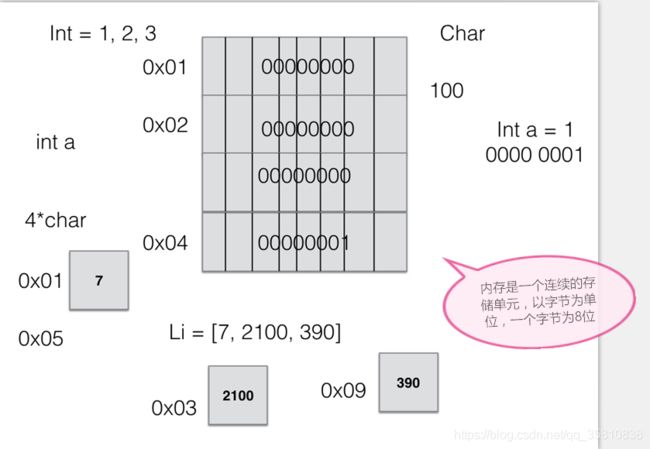
七。内存
所说的类型,就是需要占用几个字节的内存大小(类型不同占用的空间也不同) --------存
我取出的数个字节以什么样的类型来对待。int 4个字节 char 1个字节
所有的高级数据结构都是有基本的数据结构构成
比如 int 占用四个字节 int 1 在内存中存储的形式为 00000000 00000000 00000000 00000001
八。顺序表
将数据存放在内存中的一段连续的空间上
图a表示的是顺序表的基本形式,数据元素本身连续存储,每个元素所占的存储单元大小固定相同(数据类型相同),元素的下标是其逻辑地址,而元素存储的物理地址(实际内存地址)可以通过存储区的起始地址Loc (e0)加上逻辑地址(第i个元素)与存储单元大小(c)的乘积计算而得,即:
Loc(ei) = Loc(e0) + c*i
故,访问指定元素时无需从头遍历,通过计算便可获得对应地址,其时间复杂度为O(1)。
如果元素的大小不统一,则须采用图b的元素外置的形式,将实际数据元素另行存储,而顺序表中各单元位置保存对应元素的地址信息(即链接)。由于每个链接所需的存储量相同,通过上述公式,可以计算出元素链接的存储位置,而后顺着链接找到实际存储的数据元素。注意,图b中的c不再是数据元素的大小,而是存储一个链接地址所需的存储量,这个量通常很小。
图b这样的顺序表也被称为对实际数据的索引,这是最简单的索引结构。
0下标可以理解为偏移量,这样在寻址的时候特方便
顺序表结构
一个顺序表的完整信息包括两部分,一部分是表中的元素集合,另一部分是为实现正确操作而需记录的信息,即有关表的整体情况的信息,这部分信息主要包括元素存储区的容量和当前表中已有的元素个数两项。
顺序表的两种基本方式
图a为一体式结构,存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。
一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储区就固定了。
图b为分离式结构,表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一个独立的元素存储区里,通过链接与基本表对象关联。
元素存储区替换
一体式结构由于顺序表信息区与数据区连续存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。
分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
元素存储区扩充
采用分离式结构的顺序表,若将数据区更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数据存储区进行了扩充,所有使用这个表的地方都不必修改。只要程序的运行环境(计算机系统)还有空闲存储,这种表结构就不会因为满了而导致操作无法进行。人们把采用这种技术实现的顺序表称为动态顺序表,因为其容量可以在使用中动态变化。
扩充的两种策略
-
每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。
特点:节省空间,但是扩充操作频繁,操作次数多。
-
每次扩充容量加倍,如每次扩充增加一倍存储空间。
特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式。
顺序表的操作
插入 1)对未插入 2)保序插入 O(n) 3)不保序插入
删除 2)对尾删除 2)保序删除 3)不保序删除
Python中的顺序表
Python中的list和tuple两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的所有性质。
tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性质类似。
list的基本实现技术
Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的顺序(即保序),而且还具有以下行为特征:
-
基于下标(位置)的高效元素访问和更新,时间复杂度应该是O(1);
为满足该特征,应该采用顺序表技术,表中元素保存在一块连续的存储区中。
-
允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变。
为满足该特征,就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分离式实现技术。
在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) (或 list.insert(len(list), x),即尾部插入)比在指定位置插入元素效率高的原因。
在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。