使用cuda C完成矩阵相乘算法详解

写在前面：

• 本笔记为 NVIDIA CUDA初级教程视频的笔记
• 视频连接：https://www.bilibili.com/video/BV1kx411m7Fk?p=10
• P9和P10讲解了矩阵相乘的cuda 实现
  

使用cuda C完成矩阵相乘算法详解

---

矩阵相乘大家应该都不陌生。

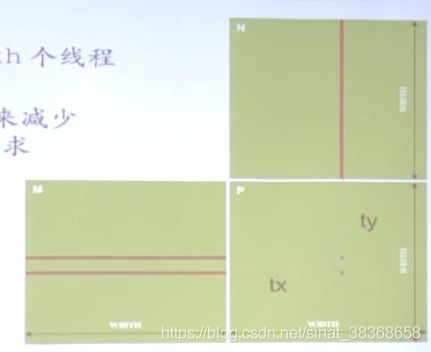
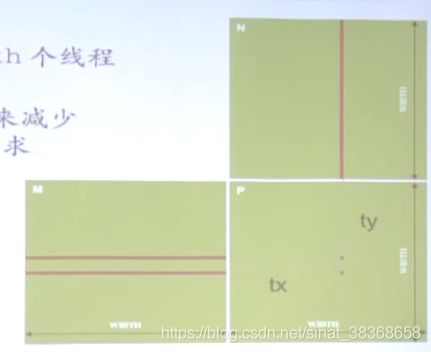
设有两个矩阵M和N，假设M和N都是方阵，维度均为width × width

如果M和N均为1000 × 1000的矩阵，总共要进行1000000次点乘。其中，每次点乘有1000次乘法和1000次加法。

Matirx Multiply：CPU实现

---

先来看看使用普通的c代码在CPU端如何实现

void MatrixMulOnHost(float* M,float* N,float* P,int width)
{
     
    for(int i=0;i<width;++i)
        for(int j=0;i<width;j++)
        {
     
            //sum对应每一次点乘（M的某一行×N的某一列）的结果
            float sum = 0;
            for(int k=0;k<width;k++)
            {
     
                float a = M[i*width+k];
                float b = N[k*width+j];
                sum+=a*b;
            }
            P[i*width+j]=sum;//乘累加的结果放到对应位置上
        }
}

可以看到循环计算结果P矩阵里的每一个元素。计算过程非常清晰。

从这里可以看到，这个计算存在非常大的并行性，即结果矩阵P里的每一个元素结果的计算与P中其他元素是不相关的，没有依赖性。

所以我们可以在GPU端上实现矩阵相乘。

Matirx Multiply：GPU实现

---

可以看到总共有3步：

1. 管理内存（在GPU上分配空间，将CPU端数据拷贝到GPU端）
2. GPU上并行处理（启动kernel函数）
3. 将结果拷贝回到CPU端

第1步：在算法框架中添加 CUDA memory transfers

第2步：CUDA C编程实现kernel

可以看到这里有2个问题

1. 使用线程的索引代替了双重循环，并行去做就可以
2. 不需要锁或同步，如果数据之间有依赖，存在同步问题，但这里每一个结果矩阵的元素是独立的，与别的元素无关，所以不需要锁存。

第3步 CUDA C编程调用kernel

源代码

#include 
#include 
#include 
#include 

#define WIDTH 16

__global__ void MatrixMulKernel(float* Md, float* Nd, float* Pd, int width)
{
     
	int tx = threadIdx.x;
	int ty = threadIdx.y;

	float Pvalue = 0;

	for (int k = 0; k<width; k++)
	{
     
		float Mdelement = Md[ty*width + k];
		float Ndelement = Nd[k*width + tx];
		Pvalue += Mdelement * Ndelement;
	}
	Pd[ty*width + tx] = Pvalue;
}

int main(void)
{
     
	float M[16][16], N[16][16], P[16][16];
	int Width = 16;
	int NUM = 192;
	//初始化示例数据
	for (int i = 0; i<16; i++)
	{
     
		for (int j = 0; j<16; j++)
		{
     
			M[i][j] = 2.0;
			N[i][j] = 3.0;
		}
	}
	int size = Width*Width*sizeof(float);

	float *Md, *Nd, *Pd;
	cudaMalloc((void**)&Md, size);
	cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
	cudaMalloc((void**)&Nd, size);
	cudaMemcpy(Nd, N, size, cudaMemcpyHostToDevice);
	cudaMalloc((void**)&Pd, size);

	dim3 dimBlock(WIDTH, WIDTH);
	dim3 dimGrid(1, 1);
	MatrixMulKernel <<<dimGrid, dimBlock >> >(Md, Nd, Pd, Width);

	cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);

	//打印结果矩阵
	for (int i = 0; i<16; i++)
	{
     
		for (int j = 0; j<16; j++)
		{
     
			printf("%.2f  ", P[i][j]);
		}
		printf("\n");
	}

	cudaFree(Md);
	cudaFree(Nd);
	cudaFree(Pd);

	return 0;
}

回顾一下并行实现这个样例的原理：

在这个矩阵相乘的案例中：

1. 在算法实现中最主要的性能问题是什么？
   • 矩阵长度限制
     • 仅有一个block
     • 以G80和GT200为例 —— 最多512个线程/block
2. 主要的限制是什么？
   • 很多global memory读写访问（读Md，Nd，两次读后才写一次，这两次读耗时巨大，开销较大）

优化矩阵相乘（一） —— 去除长度限制

解决第一个问题：去除长度限制

• 将Pd矩阵拆成tile小块
• 把一个tile布置到一个block
• 通过threadIdx和blockIdx索引

由于计算结果依然是彼此独立的，所以每个block可以自己做自己的事情。

优化后的kernel函数如下：

（注意：每个线程计算的是块内子矩阵的一个元素）

__global__ void MatrixMulKernel_01(float* Md, float* Nd, float* Pd, int width)
{
     
	//计算矩阵Pd和M的行索引
	int Row = blockIdx.y*blockDim.y + threadIdx.y;
	//计算矩阵Pd和N的列索引
	int Col = blockIdx.x*blockDim.x + threadIdx.x;

	float Pvalue = 0;

	//每个线程计算块内子矩阵的一个元素
	for (int k = 0; k<width; k++)
	{
     
		float Mdelement = Md[Row*width + k];
		float Ndelement = Nd[k*width + Col];
		Pvalue += Mdelement * Ndelement;
	}
	Pd[Row*width + Col] = Pvalue;
}

这种方式可以适用于大规模的问题

调用kernel代码如下：

dim3 dimGrid(Width / TILE_WIDTH, Height / TILE_WIDTH);
dim3 dimBlock(TILE_WIDTH, TILE_WIDTH);
MatrixMulKernel_01 <<<dimGrid, dimBlock >> >(Md, Nd, Pd, TILE_WIDTH);

注：如果输入的数组不是TILE_WIDTH的整数倍怎么办？扩充元素到分块的整数倍后将元素填0

优化矩阵相乘（二） —— 使用共享内存

上述代码访存受限与global memory带宽

• G80 峰值GFLOPS：346.4
• 需要1386 GB/s（每个浮点数4个bit，346*4）的带宽未达到
• G80 存储器实际带宽：86.4GB/s
  • 限制代码 21.6 GFLOPS
  • 实际上，代码运行速度是15 GLOPS
• 必须大幅减少对global memory的访问

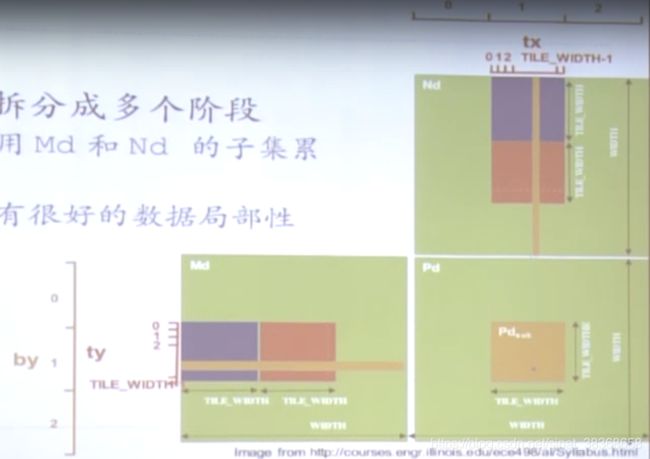
回顾之前的程序，实际上，每个输入元素被Width个线程读取（对于每一列都读取了Width次），所以使用shared memory来减少global memory带宽需求。

把kernel拆分成多个阶段

• 每个阶段用Md和Nd的子集累加Pd
• 每个阶段有很好的数据局部性

每个线程

• 读入瓦片内Md和Nd的一个元素存入shared memory

代码如下：

__global__ void MatrixMulKernel_01(float* Md, float* Nd, float* Pd, int width)
{
     
	//块内定义shared memory存储Md和Nd的子集
	__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
	__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];

	int bx = blockIdx.x; int by = blockIdx.y;
	int tx = threadIdx.x; int ty = threadIdx.y;

	int Row = by*TILE_WIDTH + ty;
	int Col = bx*TILE_WIDTH + tx;

	float Pvalue = 0;
	//注：多个块的计算的结果相加后才得到pd对应元素的值
	//width/TILE_WIDTH：阶段数目
	//m:当前阶段的索引
	for (int m = 0; m<width/TILE_WIDTH; m++)
	{
     
		//从Md和Nd各取一个元素存入shared memory
		Mds[ty][tx] = Md[Row*width + (m*TILE_WIDTH + tx)];
		Nds[ty][tx] = Nd[Col + (m*TILE_WIDTH + ty)*width];
		//等待block内所有线程，即等到整个瓦片存入shared memory
		__syncthreads();

		//累加点乘的子集
		for (int k = 0; k < TILE_WIDTH; k++)
			Pvalue += Mds[ty][k] * Nds[k][tx];
		//注：如果没有同步，可以上一次的乘累加没完成，下一次的数已经过来把乘累加结果冲掉了
		__synthreads();
	}
	//把最终结果写入global memory
	Pd[Row*width + Col] = Pvalue;
}

如何选取TITLE_WIDTH的数值？

• 如果太大的话会怎样？

  • 超出一个块允许的最大线程数

  ​ Fermi — 1024；Kerpler - 1024；具体根据不同的计算能力查表得到。

  • 超出shared memory极限

  ​ 以G80为例：16KM/SM 并且 B blocks/SM；

  ​ 2KB/block

  ​ 1KB给Nds，1KB给Mds（16 * 16 *4）

  ​ TITLE_WIDTH = 16

  ​ 更大的TITLE_WIDTH将导致更少的块数

Shared memory瓦片化的好处

• global memory 访问次数减少TILE_WIDTH倍
  • 16*16瓦片 减少16倍
• 以G80为例
  • 现在global memory 支持345.6 GFLOPS
  • 接近峰值 346.5 GFLOPS

G80线程尺寸的考虑

• 每个thread block有许多个线程
  • TILE_WIDTH为16时：16*16=256个线程
• 需要许多个thread blocks
  • 一个1024*1024 Pd 需要：64 * 64 = 4K thread blocks
• 每个thread block执行 2*256 =512次global memory的float读入，为了供应256 *（2 *16）= 8K mul/add操作
  • 存储带宽不再是限制因素

Atomic Functions 原子操作

• 许多原子操作

//算数运算
atomicAdd();
atomicSub();
atomicExch();
atomicMin();
atomicMax();
atomicDec();
atomicCAS();

//位运算
atomicAnd();
atomicOr();
atomicXor();

• 不同块里面的线程如何协作？
  • CUDA中的线程协作主要是通过共享内存实现的。使用关键字**“share”**声明共享变量
  • 共享内存是用于同一个线程块内的线程之间交流的，不同线程块之间是无法通过共享内存进行交流的
  • 还有更多内容待补充。
• 尽量少用原子操作，为什么？
  • 原子操作比较耗时，需要在整个系统里进行排队

优化的矩阵乘法源代码

#include 
#include 
#include 
#include 

/*
 * 去除长度限制 & 使用共享内存 的矩阵相乘优化
*/

#define TILE_WIDTH 8

__global__ void MatrixMulKernel_01(float* Md, float* Nd, float* Pd, int width)
{
     
	//块内定义shared memory存储Md和Nd的子集
	__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
	__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];

	int bx = blockIdx.x; int by = blockIdx.y;
	int tx = threadIdx.x; int ty = threadIdx.y;

	int Row = by*TILE_WIDTH + ty;
	int Col = bx*TILE_WIDTH + tx;

	float Pvalue = 0;
	//注：多个块的计算的结果相加后才得到pd对应元素的值
	//width/TILE_WIDTH：阶段数目
	//m:当前阶段的索引
	for (int m = 0; m<width/TILE_WIDTH; m++)
	{
     
		//从Md和Nd各取一个元素存入shared memory
		Mds[ty][tx] = Md[Row*width + (m*TILE_WIDTH + tx)];
		Nds[ty][tx] = Nd[Col + (m*TILE_WIDTH + ty)*width];
		//等待block内所有线程，即等到整个瓦片存入shared memory
		__syncthreads();

		//累加点乘的子集
		for (int k = 0; k < TILE_WIDTH; k++)
			Pvalue += Mds[ty][k] * Nds[k][tx];
		//注：如果没有同步，可以上一次的乘累加没完成，下一次的数已经过来把乘累加结果冲掉了
		__syncthreads();
	}
	//把最终结果写入global memory
	Pd[Row*width + Col] = Pvalue;
}

int main(void)
{
     
	float M[16][16], N[16][16], P[16][16];
	int Width = 16;
	int Height = 16;
	//初始化示例数据
	for (int i = 0; i<16; i++)
	{
     
		for (int j = 0; j<16; j++)
		{
     
			M[i][j] = 2.0;
			N[i][j] = 3.0;
		}
	}
	int size = Width*Height*sizeof(float);

	float *Md, *Nd, *Pd;
	cudaMalloc((void**)&Md, size);
	cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
	cudaMalloc((void**)&Nd, size);
	cudaMemcpy(Nd, N, size, cudaMemcpyHostToDevice);
	cudaMalloc((void**)&Pd, size);

	dim3 dimGrid(Width / TILE_WIDTH, Height / TILE_WIDTH);
	dim3 dimBlock(TILE_WIDTH, TILE_WIDTH);
	MatrixMulKernel_01 <<<dimGrid, dimBlock >> >(Md, Nd, Pd, Width);

	cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);

	//打印结果矩阵
	for (int i = 0; i<16; i++)
	{
     
		for (int j = 0; j<16; j++)
		{
     
			printf("%.2f  ", P[i][j]);
		}
		printf("\n");
	}

	cudaFree(Md);
	cudaFree(Nd);
	cudaFree(Pd);

	return 0;
}