rm(list = ls())
mean(mtcars$gear)
median(mtcars$gear)
[1] 4
par(mfrow=c(3,1)) # 几行几列
curve(dnorm(x),-1,1) # curve(函数, 范围)绘制曲线
curve(dnorm(x),-5,5) # dnorm
curve(sin, -2*pi, 2*pi)
# 使用到par()函数定义一页多图
#par(mfrow=c(1,2)) #一页两幅图
#mfrow=c(2,2) 画4幅图,两行两列
#mfrow=c(3,5) 画15幅图,三行五列
dnorm(x, mean = 0, sd = 1, log = FALSE) 的返回值是正态分布概率密度函数值,比如dnorm(z)则表示:标准正态分布密度函数f(x)在x=z处的函数值。
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) 返回值是正态分布的分布函数值,比如pnorm(z)等价于P[X ≤ z]
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) 的返回值是给定概率p后的下分位点.
rnorm(n, mean = 0, sd = 1) 的返回值是n个正态分布随机数构成的向量。
curve(dnorm(x), xlim = c(-2, 2),ylab="",axes=FALSE)
abline(h = 3, col='red') # 函数的作用是在一张图表上添加直线
axis(1, at=c(-2,-1,0,0.8,1,2), pos=0)
# axis
# 第一个参数 side表示要操作的坐标轴,取值1、2、3、4分别代表下、左、上、右;
# at表示刻度线及刻度值所在位置;
# pos 表示轴线所在的位置;
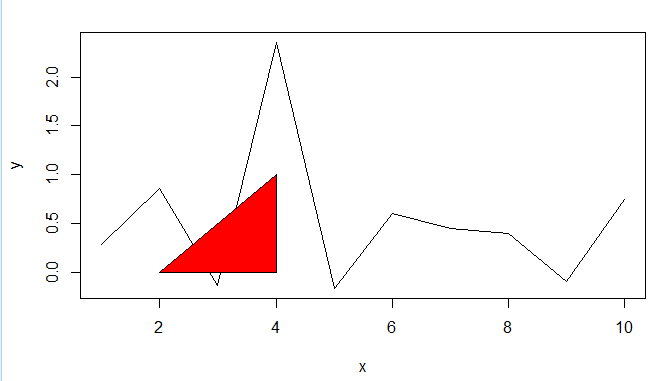
图形填充颜色(polygon函数)
- 以数据(x,y)为坐标,依次连接所有的点,绘出一个多边形
x = 1:10
y = rnorm(x)
x1 = c(2, 4, 4)
y1 = c(0, 0, 1)
plot(x, y, type = 'l')
polygon(x1, y1, col = 'red')
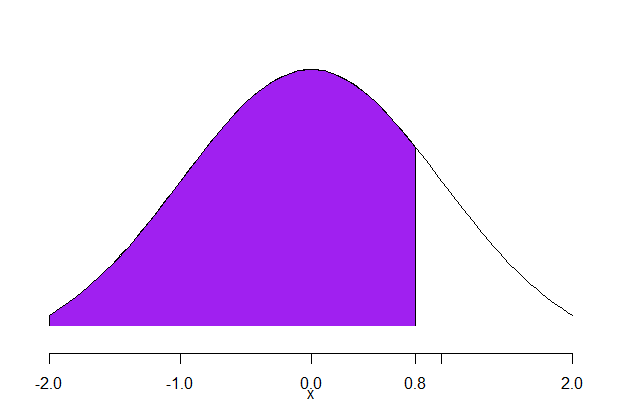
curve(dnorm(x), xlim = c(-2, 2),ylab="",axes=FALSE)
abline(h = 3, col='red') # 函数的作用是在一张图表上添加直线
sequence = seq(-2, 0.8, 0.1)
polygon(x = c(sequence,0.8,-2),
y = c(dnorm(c(sequence)),0,0),
col = "purple")
axis(1, at=c(-2,-1,0,0.8,1,2), pos=0)
# axis
# 第一个参数 side表示要操作的坐标轴,取值1、2、3、4分别代表下、左、上、右;
# at表示刻度线及刻度值所在位置;
# pos 表示轴线所在的位置;
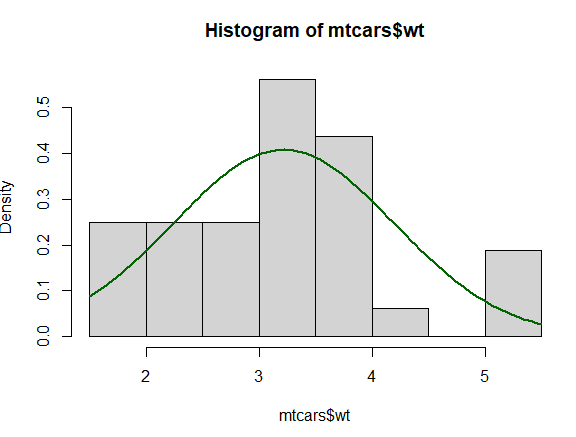
hist(mtcars$wt,prob=T) # prob=T指定为频率
m=mean(mtcars$wt) # 求均值
s=sd(mtcars$wt) # 方差
curve(dnorm(x, mean=m, sd=s), col="darkgreen", lwd=2, add=TRUE ) # lwd=2线的宽度
# add=TRUE 代表加载直方图上