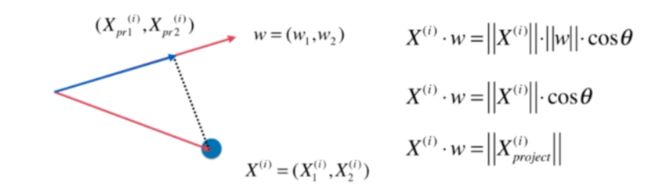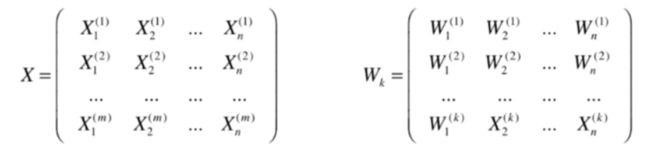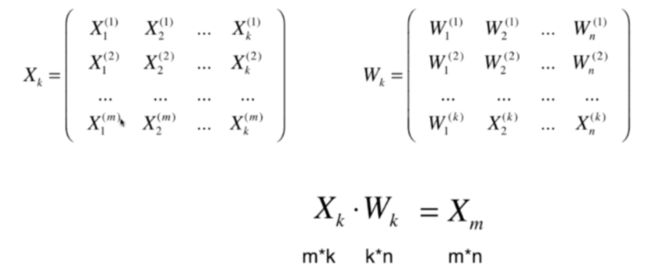主成分分析(PCA)是最常见的降维算法。
- PCA是非监督的机器学习算法
- 主要用于数据的降维
- 其他应用:可视化、去噪
1 什么是PCA
1.1 分析
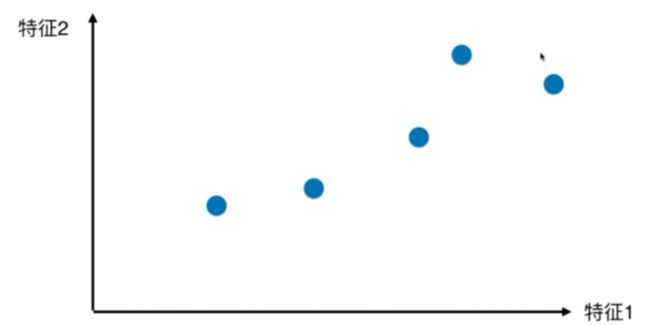
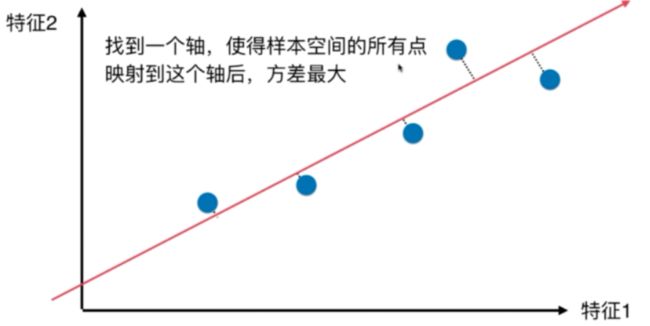
上图为数据在2个特征维度的分布情况,分别垂直到X轴、Y轴,这是两个维度,从上图中来看,无法说明这两个维度哪个更好。那么能否找到一个轴,使得投射到此轴的上的点,间距要比投射到X轴、Y轴间距更大(区分度更高)。如下图:
- 那么如何找到这个让样本间间距最大的轴?
- 如何定义样本间间距?
使用方差,
1.2步骤
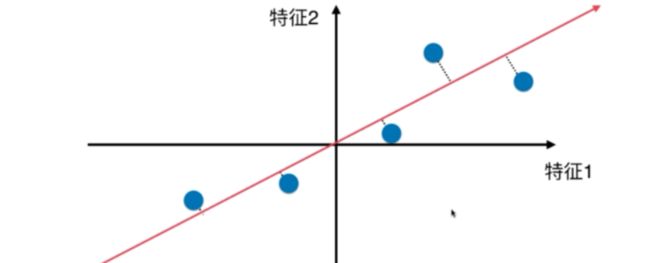
- 将样本的均值归0(demean),转化后如下图,此时
- 求一个轴的方向,使得所有样本映射到w以后,下面值更大
归0化之后,,此时转化为求下面式子最大值
令为一个单位向量
1.3 目标函数
目标:求w,使得下值最大
- 一个目标函数的最优化问题,使用梯度上升法解决
1.4 PCA与线性回归的区别
- PCA是找到一个轴,使得样本空间点映射到这个轴后方差最大。
- 线性回归尝试的是最小化预测误差。
- 线性回归的目的是预测结果,而主成分分析不作任何预测。
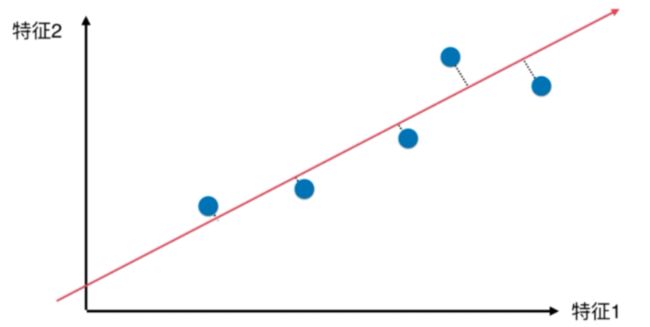
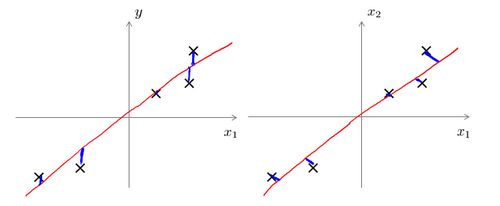
上图中,左边的是线性回归的误差(垂直于横轴投影),右边则是主要成分分析(垂直于红线投影)。
2 梯度上升法求PCA问题
2.1 推导过程
目标:求w,使得下值最大
求梯度▽f,转化为向量点乘的过程:w是列向量,X是m*n维矩阵
2.2 代码实现
def demean(X):
"""均值归0化"""
# 减去每一列的均值
return X - np.mean(X, axis=0)
def f(w, X):
"""目标函数"""
return np.sum((X.dot(w)**2)) / len(X)
def df_math(w, X):
"""梯度公式"""
return X.T.dot(X.dot(w)) * 2. / len(X)
def df_debug(w, X, epsilon=0.0001):
"""梯度调试,因为w是单位向量,比较小,因此epsilon也应该小一些"""
res = np.empty(len(w))
for i in range(len(w)):
w_1 = w.copy()
w_1[i] += epsilon
w_2 = w.copy()
w_2[i] -= epsilon
res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
return res
def direction(w):
"""让w为单位向量"""
return w / np.linalg.norm(w)
def first_component(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):
"""梯度上升法求w"""
# 几个注意点:
# 1、w初始向量不能为0向量
# 2、不能使用StandardScalar 标准化数据 ,因为我们要求这个轴的最大方差,如果使用标准化,方差就为1了,就不存在最大方差了
w = direction(initial_w) # 注意,w初始向量不能为0向量
cur_iter = 0
while cur_iter < n_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w) # 注意3:每次求一个单位方向
if(abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iter += 1
return w
2.3 前n个主成分
求出第一主成分之后,如何求下一个主成分?
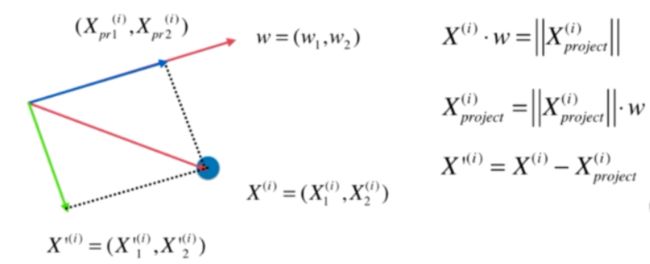
答:将数据在第一个主成分上的分量去掉
如下图:即为下一个主成分
def first_n_components(n, X, eta=0.01, n_iters = 1e4, epsilon=1e-8):
"""求前n个主成分"""
X_pca = X.copy()
X_pca = demean(X_pca) # 归0化
res = [] # 记录前n个主成分
for i in range(n):
initial_w = np.random.random(X_pca.shape[1])
w = first_component(X_pca, initial_w, eta)
res.append(w)
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w # 去除上一个主成分分量
return res
3 高维数据向低维数据映射
3.1 映射分析
为前k个主成分,,就完成了n个维度向k个维度的映射
当然,也可以反向映射,由低维数据映射到高维数据,但是此时会有信息丢失
3.2 PCA的封装
import numpy as np
class PCA:
def __init__(self, n_components):
"""初始化PCA"""
assert n_components >= 1
self.n_components = n_components
self.components_ = None # 前n个主成分
def fit(self, X, eta=0.01, n_iters=1e4):
"""获得数据集X的前n个主成分"""
assert self.n_components <= X.shape[1]
def demean(X):
return X - np.mean(X, axis=0)
def f(w, X):
return np.sum((X.dot(w) ** 2)) / len(X)
def df(w, X):
return X.T.dot(X.dot(w)) * 2. / len(X)
def direction(w):
return w / np.linalg.norm(w)
def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if (abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iter += 1
return w
X_pca = demean(X)
self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
for i in range(self.n_components):
initial_w = np.random.random(X_pca.shape[1])
w = first_component(X_pca, initial_w, eta, n_iters)
self.components_[i,:] = w
X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
return self
def transform(self, X):
"""将给定的X,映射到各个主成分分量中"""
assert X.shape[1] == self.components_.shape[1]
return X.dot(self.components_.T)
def inverse_transform(self, X):
"""将给定的X,反向映射回原来的特征空间"""
assert X.shape[1] == self.components_.shape[0]
return X.dot(self.components_)
def __repr__(self):
return "PCA(n_components=%d)" % self.n_components
3.3 降到多少维才好
我们先看下问题的产生过程:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
digits = datasets.load_digits()
X = digits.data
y = digits.target
# X_train.shape = (1347, 64)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# %%time 使用kNN算法,时间64.5 ms
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test) #0.98666666666666669
"""使用PCA之后"""
pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
# %%time 时间为2.93 ms,时间大大节省
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test) #0.60666666666666669
原来有64维度,如果降到2维,时间虽然提高了,但是精度却降低的太多了,那么应该降维到多少为好呢?
sklearn 中提供了一个方法
pca.explained_variance_ratio_ # array([ 0.14566817, 0.13735469])
# 表示2个主成分 分别能代表14.5%的方差和13.7%的方差
下面打印所有维度能代表方差的维度
from sklearn.decomposition import PCA
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_
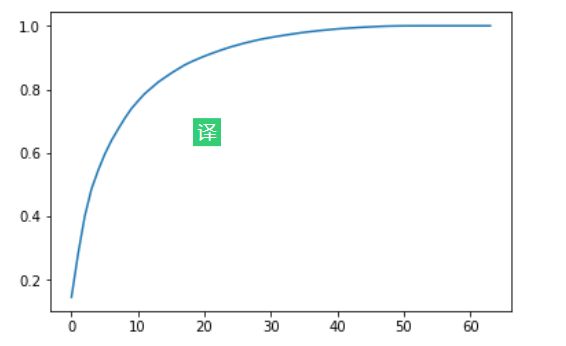
我们绘制成图像
plt.plot([i for i in range(X_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()
sklearn 中又提供了一个方法,输入参数为保留多少方差
pca = PCA(0.95)
pca.fit(X_train)
pca.n_components_ # 28
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
# %%time 19.7 ms
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test) #0.97999999999999998
4 总结
降维的过程可以理解成是去噪。
降维去除了噪音,有可能准确率更高!
PCA将n个特征降维到k个,可以用来进行数据压缩,如果100维的向量最后可以用10维来表示,那么压缩率为90%。
PCA对数据降维可以简化模型或是对数据进行压缩,同时最大程度的保持了原有数据的信息。
PCA是完全无参数限制的。计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
声明:此文章为本人学习笔记,课程来源于慕课网:python3入门机器学习经典算法与应用。在此也感谢bobo老师精妙的讲解。
如果您觉得有用,欢迎关注我的公众号,我会不定期发布自己的学习笔记、AI资料、以及感悟,欢迎留言,与大家一起探索AI之路。