2020后端面试，算法篇

2019.12-2020.02后端面试材料分享，算法篇。

拿到了字节offer，走完了Hello单车和达达的面试流程（没给offer），蚂蚁的前三轮（接了字节Offer，放弃后续流程）。

按照九章归纳的算法题出现的频率准备的：

红(高频)到灰(低频)

但后来发现九章主要是针对硅谷系的公司，算法要求普遍比较高。国内的即使是大公司，难度也低很多，把经典的数据结构、经典的算法搞清楚，10-20分钟内能搞定leetcode上简单难度的题，即可。

掌握套路是很重要的，因为对工程师的要求是熟悉“应用”，而不是“发明”，套路没get情况下，硬啃会浪费大量时间。我的方式是，最开始把leetcod上简单级别的题目，全看一遍，只看不写，没想法的、思路不优化的，说明对背后的套路尚不熟悉，应该先熟悉一遍，然后再上手写代码，提高算法落低和bug-free能力。推荐多看看别人的总结，比如：

• 二分法套路
• 动态规范套路
• 回溯算法套路

以下清单是当时看完后没有立刻来思路的题目(来自leetcode)。思路的掌握涉及记忆，我希望根据遗忘曲线来安排学习进度和复习计划。于是便有了这个类anki的小程序：一进制。默认隐藏答案，思考后再点开对照；根据你反馈的难度，安排复习时间。

“一进制”，算法篇

-问题1: 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:
输入:["flower","flow","flight"] 输出: "fl"
示例 2:
输入:["dog","racecar","car"] 输出: "" 解释: 输入不存在公共前缀。
说明:

所有输入只包含小写字母 a-z 。

-tags: 字符串,算法

-解答:

方法一：水平扫描

首先，我们将描述一种查找一组字符串的最长公共前缀 LCP(S_1 ... S_n) 的简单方法。
我们将会用到这样的结论：

LCP(S_1 ... S_n) = LCP(LCP(LCP(S_1, S_2),S_3), ... S_n)

为了运用这种思想，算法要依次遍历字符串 [S_1 ... S_n]，当遍历到第i个字符串的时候，找到最长公共前缀 LCP(S_1 ... S_i)。当它是一个空串的时候，算法就结束了。 否则，在执行了n次遍历之后，算法就会返回最终答案。

public String longestCommonPrefix(String[] strs) {
   if (strs.length == 0) return "";
   String prefix = strs[0];
   for (int i = 1; i < strs.length; i++)
       while (strs[i].indexOf(prefix) != 0) {
           prefix = prefix.substring(0, prefix.length() - 1);
           if (prefix.isEmpty()) return "";
       }        
   return prefix;
}

复杂度分析

• 时间复杂度：O(S)，S 是所有字符串中字符数量的总和。

• 最坏的情况下，n个字符串都是相同的。算法会将 S1 与其他字符串 [S_2 .._n] 都做一次比较。这样就会进行 S次字符比较，其中 S 是输入数据中所有字符数量。

• 空间复杂度：O(1)，我们只需要使用常数级别的额外空间。

算法二：水平扫描2

想象数组的末尾有一个非常短的字符串，使用上述方法依旧会进行 `S​ 次比较。优化这类情况的一种方法，我们从前往后枚举字符串的每一列，先比较每个字符串相同列上的字符（即不同字符串相同下标的字符）然后再比较下一列。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";
    for (int i = 0; i < strs[0].length() ; i++){
        char c = strs[0].charAt(i);
        for (int j = 1; j < strs.length; j ++) {
            if (i == strs[j].length() || strs[j].charAt(i) != c)
                return strs[0].substring(0, i);             
        }
    }
    return strs[0];
}

复杂度分析

• 时间复杂度：O(S)，S 是所有字符串中字符数量的总和。

  • 最坏情况下，输入数据为 n个长度为 m 的相同字符串，算法会进行 S = mn 次比较。可以看到最坏情况下，本算法的效率与算法一相同，但是最好的情况下，算法只需要进行 nminLen 次比较，其中 minLen 是数组中最短字符串的长度。

• 空间复杂度：O(1)，我们只需要使用常数级别的额外空间。

算法三：分治

这个算法的思路来自于LCP操作的结合律。 我们可以发现：
LCP(S_1 ... S_n) = LCP(LCP(S_1 ... S_k), LCP (S_{k+1} ... S_n))
，其中 LCP(S_1 ... S_n) 是字符串 [S_1 ... S_n] 的最长公共前缀，1 < k < n。

为了应用上述的结论，我们使用分治的技巧，将原问题分成两个子问题 LCP(S_i, S_{mid}) 与 LCP(S_{mid+1}, S_j) ，其中 mid = (i + j) / 2。 我们用子问题的解 lcpLeft 与 lcpRight 构造原问题的解 LCP(S_i ... S_j)。 从头到尾挨个比较 lcpLeft 与 lcpRight 中的字符，直到不能再匹配为止。 计算所得的 lcpLeft 与 lcpRight 最长公共前缀就是原问题的解。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";    
        return longestCommonPrefix(strs, 0 , strs.length - 1);
}

private String longestCommonPrefix(String[] strs, int l, int r) {
    if (l == r) {
        return strs[l];
    }
    else {
        int mid = (l + r)/2;
        String lcpLeft =   longestCommonPrefix(strs, l , mid);
        String lcpRight =  longestCommonPrefix(strs, mid + 1,r);
        return commonPrefix(lcpLeft, lcpRight);
   }
}

String commonPrefix(String left,String right) {
    int min = Math.min(left.length(), right.length());       
    for (int i = 0; i < min; i++) {
        if ( left.charAt(i) != right.charAt(i) )
            return left.substring(0, i);
    }
    return left.substring(0, min);
}

复杂度分析

最坏情况下，我们有 n 个长度为 m的相同字符串。

• 时间复杂度：O(S)，S 是所有字符串中字符数量的总和，S=mn*。最好情况下，算法会进行 次比较，其中 是数组中最短字符串的长度。

• 空间复杂度：O(m * log(n))
  内存开支主要是递归过程中使用的栈空间所消耗的。 一共会进行 log(n) 次递归，每次需要 m 的空间存储返回结果，所以空间复杂度为 O(m * log(n))。

方法四：二分查找法

这个想法是应用二分查找法找到所有字符串的公共前缀的最大长度 L。 算法的查找区间是 (0 ... minLen)，其中 minLen 是输入数据中最短的字符串的长度，同时也是答案的最长可能长度。 每一次将查找区间一分为二，然后丢弃一定不包含最终答案的那一个。算法进行的过程中一共会出现两种可能情况：

• S[1...mid] 不是所有串的公共前缀。 这表明对于所有的 j > i S[1..j] 也不是公共前缀，于是我们就可以丢弃后半个查找区间。

• S[1...mid] 是所有串的公共前缀。 这表示对于所有的 i < j S[1..i] 都是可行的公共前缀，因为我们要找最长的公共前缀，所以我们可以把前半个查找区间丢弃。

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0)
        return "";
    int minLen = Integer.MAX_VALUE;
    for (String str : strs)
        minLen = Math.min(minLen, str.length());
    int low = 1;
    int high = minLen;
    while (low <= high) {
        int middle = (low + high) / 2;
        if (isCommonPrefix(strs, middle))
            low = middle + 1;
        else
            high = middle - 1;
    }
    return strs[0].substring(0, (low + high) / 2);
}

private boolean isCommonPrefix(String[] strs, int len){
    String str1 = strs[0].substring(0,len);
    for (int i = 1; i < strs.length; i++)
        if (!strs[i].startsWith(str1))
            return false;
    return true;
}

复杂度分析
最坏情况下，我们有 n 个长度为 m 的相同字符串。

• 时间复杂度：O(S * log(n))，其中 S所有字符串中字符数量的总和。

算法一共会进行 log(n) 次迭代，每次一都会进行 S = mn* 次比较，所以总时间复杂度为 O(S * log(n))。

• 空间复杂度：`O(1)，我们只需要使用常数级别的额外空间。

---

-问题2: x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:
输入: 4 输出: 2
示例 2:
输入: 8 输出: 2 说明: 8 的平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

-tags: 二分查找,算法,数学

-解答:

方法一：二分法

使用二分法搜索平方根的思想很简单，高了就往低了猜，低了就往高了猜，范围越来越小。因此，使用二分法猜算术平方根就很自然。

需要观察到的关键点是：一个数的平方根不会超过它的一半，因此一半可当做右值。

class Solution:
    def mySqrt(self, x: int) -> int:
        # 为了照顾到 0 把左边界设置为 0
        left = 0
        # 为了照顾到 1 把右边界设置为 x // 2 + 1
        right = x // 2 + 1
        while left < right:
            # 注意：这里一定取右中位数，如果取左中位数，代码可能会进入死循环
            # mid = left + (right - left + 1) // 2
            mid = (left + right + 1) >> 1
            square = mid * mid

            if square > x:
                right = mid - 1
            else:
                left = mid
        # 因为一定存在，因此无需后处理
        return left

方法二：牛顿法

使用牛顿法可以得到一个正实数的算术平方根，因为题目中说“结果只保留整数部分”，因此，我们把使用牛顿法得到的浮点数转换为整数即可。

这里给出牛顿法的思想：

在迭代过程中，以直线代替曲线，用一阶泰勒展式（即在当前点的切线）代替原曲线，求直线与 x 轴的交点，重复这个过程直到收敛。

class Solution:

    def mySqrt(self, x):
        if x < 0:
            raise Exception('不能输入负数')
        if x == 0:
            return 0
        # 起始的时候在 1 ，这可以比较随意设置
        cur = 1
        while True:
            pre = cur
            cur = (cur + x / cur) / 2
            if abs(cur - pre) < 1e-6:
                return int(cur)

---

-问题3: 二叉树的层次遍历 II

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

例如：
给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7
返回其自底向上的层次遍历为：
[ [15,7], [9,20], [3] ]

-tags: 广度优先搜索,算法,树

-解答:
先从顶部遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector> levelOrderBottom(TreeNode* root) {
        vector> res;
        levelorder(root,0,res);
        return vector>(res.rbegin(),res.rend());
    }
        
    void levelorder(TreeNode* node, int level, vector>& res) 
    {
        if(!node) return ;
        if(res.size()==level) res.push_back({});
        res[level].push_back(node->val);
        if(node->left) levelorder(node->left,level+1, res);
        if(node->right) levelorder(node->right,level+1,res);
    }
};

---

-问题4: 买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:
输入: [7,1,5,3,6,4] 输出: 5 解释:在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1] 输出: 0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。

-tags: 数组,动态规划,算法

-解答:

解决方案

我们需要找出给定数组中两个数字之间的最大差值（即，最大利润）。此外，第二个数字（卖出价格）必须大于第一个数字（买入价格）。

形式上，对于每组 和 （其中 ）我们需要找出 。

方法一：暴力法

public class Solution {
    public int maxProfit(int prices[]) {
        int maxprofit = 0;
        for (int i = 0; i < prices.length - 1; i++) {
            for (int j = i + 1; j < prices.length; j++) {
                int profit = prices[j] - prices[i];
                if (profit > maxprofit)
                    maxprofit = profit;
            }
        }
        return maxprofit;
    }
}

复杂度分析

• 时间复杂度：。循环运行 次。
• 空间复杂度：。只使用了两个变量 —— 和 。

方法二：一次遍历

算法

假设给定的数组为：

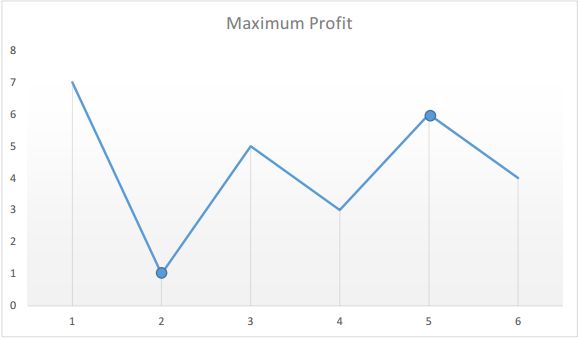
[7, 1, 5, 3, 6, 4]

如果我们在图表上绘制给定数组中的数字，我们将会得到：

Profit Graph

{:width="400px"}
{:align="center"}

使我们感兴趣的点是上图中的峰和谷。我们需要找到最小的谷之后的最大的峰。
我们可以维持两个变量——minprice 和 maxprofit，它们分别对应迄今为止所得到的最小的谷值和最大的利润（卖出价格与最低价格之间的最大差值）。

public class Solution {
    public int maxProfit(int prices[]) {
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minprice)
                minprice = prices[i];
            else if (prices[i] - minprice > maxprofit)
                maxprofit = prices[i] - minprice;
        }
        return maxprofit;
    }
}

复杂度分析

• 时间复杂度：，只需要遍历一次。
• 空间复杂度：，只使用了两个变量。

---

-问题5: 买卖股票的最佳时机 II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5] 输出: 4 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。 因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

-tags: 数组,算法,贪心算法

-解答:

方法一：暴力法

这种情况下，我们只需要计算与所有可能的交易组合相对应的利润，并找出它们中的最大利润。

class Solution {
    public int maxProfit(int[] prices) {
        return calculate(prices, 0);
    }

    public int calculate(int prices[], int s) {
        if (s >= prices.length)
            return 0;
        int max = 0;
        for (int start = s; start < prices.length; start++) {
            int maxprofit = 0;
            for (int i = start + 1; i < prices.length; i++) {
                if (prices[start] < prices[i]) {
                    int profit = calculate(prices, i + 1) + prices[i] - prices[start];
                    if (profit > maxprofit)
                        maxprofit = profit;
                }
            }
            if (maxprofit > max)
                max = maxprofit;
        }
        return max;
    }
}

复杂度分析

• 时间复杂度：O(n^n)，调用递归函数 n^n次。
• 空间复杂度：O(n)，递归的深度为 n。

方法二：峰谷法

假设给定的数组为：

[7, 1, 5, 3, 6, 4]，想象成高低不平的群山，那么我们的兴趣点是连续的峰和谷。

用数学语言描述为：

Total Profit= sum_{i}(height(peak_i)-height(valley_i))

关键是我们需要考虑到紧跟谷的每一个峰值以最大化利润。如果我们试图跳过其中一个峰值来获取更多利润，那么我们最终将失去其中一笔交易中获得的利润，从而导致总利润的降低。

class Solution {
    public int maxProfit(int[] prices) {
        int i = 0;
        int valley = prices[0];
        int peak = prices[0];
        int maxprofit = 0;
        while (i < prices.length - 1) {
            while (i < prices.length - 1 && prices[i] >= prices[i + 1])
                i++;
            valley = prices[i];
            while (i < prices.length - 1 && prices[i] <= prices[i + 1])
                i++;
            peak = prices[i];
            maxprofit += peak - valley;
        }
        return maxprofit;
    }
}

复杂度分析

• 时间复杂度：O(n)。遍历一次。

• 空间复杂度：O(1)。需要常量的空间。

方法三：简单的一次遍历

该解决方案遵循 方法二 的本身使用的逻辑，但有一些轻微的变化。在这种情况下，我们可以简单地继续在斜坡上爬升并持续增加从连续交易中获得的利润，而不是在谷之后寻找每个峰值。最后，我们将有效地使用峰值和谷值，但我们不需要跟踪峰值和谷值对应的成本以及最大利润，但我们可以直接继续增加加数组的连续数字之间的差值，如果第二个数字大于第一个数字，我们获得的总和将是最大利润。这种方法将简化解决方案。
这个例子可以更清楚地展现上述情况：

[1, 7, 2, 3, 6, 7, 6, 7]

class Solution {
    public int maxProfit(int[] prices) {
        int maxprofit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > prices[i - 1])
                maxprofit += prices[i] - prices[i - 1];
        }
        return maxprofit;
    }
}

复杂度分析

• 时间复杂度：O(n)$，遍历一次。
• 空间复杂度：O(1)，需要常量的空间。

---

-问题6: 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:
输入: [2,2,1] 输出: 1
示例 2:
输入: [4,1,2,1,2] 输出: 4

-tags: 算法,位运算,哈希表

-解答:

方法 1：列表操作

1. 遍历 nums 中的每一个元素
2. 如果某个 nums 中的数字是新出现的，则将它添加到列表中
3. 如果某个数字已经在列表中，删除它

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        no_duplicate_list = []
        for i in nums:
            if i not in no_duplicate_list:
                no_duplicate_list.append(i)
            else:
                no_duplicate_list.remove(i)
        return no_duplicate_list.pop()

复杂度分析

• 时间复杂度：O(n^2) 。遍历 nums花费 O(n) 的时间。还要在列表中遍历判断是否存在这个数字，花费 O(n) 的时间，所以总循环时间为 O(n^2)。
• 空间复杂度：O(n) 。我们需要一个大小为n的列表保存所有元素。

方法 2：哈希表

我们用哈希表避免每次查找元素是否存在需要的 O(n) 时间。

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        hash_table = {}
        for i in nums:
            try:
                hash_table.pop(i)
            except:
                hash_table[i] = 1
        return hash_table.popitem()[0]

方法 3：数学

观察得到以下等式：
2 * (a + b + c) - (a + a + b + b + c) = c

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        return 2 * sum(set(nums)) - sum(nums)

复杂度分析

• 时间复杂度：O(n + n) = O(n) 。sum 会调用 next 将 nums 中的元素遍历一遍。我们可以把上述代码看成 sum(list(i, for i in nums)) ，这意味着时间复杂度为 O(n) 。
• 空间复杂度： O(n + n) = O(n) 。 set 需要的空间跟 nums 中元素个数相等。

方法 4：位操作

• 如果我们对 0 和二进制位做 XOR 运算，得到的仍然是这个二进制位
• 如果我们对相同的二进制位做 XOR 运算，返回的结果是 0
• XOR 满足交换律和结合律： a xor a xor b = (a xor a) xor b = 0 xor b = b

所以我们只需要将所有的数进行 XOR 操作，得到那个唯一的数字。

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        a = 0
        for i in nums:
            a ^= i
        return a

---

-问题7: 只出现一次的数字 II

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:
输入: [2,2,3,2] 输出: 3
示例 2:
输入: [0,1,0,1,0,1,99] 输出: 99

-tags: 算法,位运算

-解答:

解题思路：

• 二进制下不考虑进位的加法：异或运算的含义是二进制下不考虑进位的加法，即：0 xor 0=0+0=0, 0 xor 1=0+1=1, 1 xor 0=1+0=1, 1 xor 1=1+1=0（不进位）。
• 三进制下不考虑进位的加法：通过定义某种运算 #，使得 0 # 1 = 1，1 # 1 = 2，2 # 1 = 0。在此运算规则下，出现了 3 次的数字的二进制所有位全部抵消为 0，而留下只出现 1 次的数字二进制对应位为 1。因此，在此运算规则下将整个 arr 中数字遍历加和，留下来的结果则为只出现 1 次的数字。

class Solution:

    def singleNumber(self, nums: [int]) -> int:

        ones, twos, threes = 0, 0, 0

        for num in nums:

            twos |= ones & num # 二进制某位出现1次时twos = 0，出现2, 3次时twos = 1；

            ones ^= num  # 二进制某位出现2次时ones = 0，出现1, 3次时ones = 1；

            threes = ones & twos # 二进制某位出现3次时（即twos = ones = 1时）three = 1，其余即出现1, 2次时three = 0；

            ones &= ~threes # 将二进制下出现3次的位置零，实现`三进制下不考虑进位的加法`；

            twos &= ~threes

        return ones

代码分析：

• ones ^= num：记录至目前元素num，二进制某位出现 1 次（当某位出现 3 次时有 ones = 1 ，与 twos = 1 共同表示“出现 3 次”）；
• twos |= ones & num：记录至目前元素num，二进制某位出现2 次 （当某位出现 2 次时，twos = 1 且 ones = 0 ）；
• threes = ones & twos：记录至目前元素num，二进制某位出现 3 次（即当 ones 和 twos 对应位同时为 1 时 three = 1 ）。
• one &= ~threes, two &= ~threes：将 ones, twos 中出现了 3 次的对应位清零，实现 “不考虑进位的三进制加法” 。

复杂度分析：

• 时间复杂度 O(N)：遍历一遍 nums 需要线性时间复杂度；
• 空间复杂度 O(1)：使用常数额外空间。

---

进一步简化：

• 以上过程本质上是通过构建 3 个变量的状态转换表来表示对应位的出现次数：使所有数字“相加”后出现 3N+1 次的位 ones = 1，出现 3N，3N+2次的位为 ones = 0。由于 three 其实是 ones & twos 的结果，因此我们可以舍弃 threes，仅使用 ones 和 twos 来记录出现次数。

某位出现	1次	2次	3次	4次	5次	6次	...
ones	1	0	0	1	0	0	...
twos	0	1	0	0	1	0	...
threes	0	0	1	0	0	1	...

class Solution:

    def singleNumber(self, nums: [int]) -> int:

        ones, twos = 0, 0

        for num in nums:

            ones = ones ^ num & ~twos

            twos = twos ^ num & ~ones

        return ones

代码分析：

• ones = ones ^ num & ~twos：
  • 当 num = 1 时，只当 ones = twos = 0 时将 ones 置 1，代表出现 3N+1 次；其余置 0，根据 twos 值分别代表出现 3N 次和 3N+2 次；
  • 当 num = 0 时，ones 不变；
• twos = twos ^ num & ~ones：
  • 当 num = 1 时，只当 ones = twos = 0 时将 twos 置 1，代表出现 3N+2 次；其余置 0，根据 ones 值分别代表出现 3N 次和 3N+1 次。
  • 当 num = 0 时，twos 不变。

---

-问题8: 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

输出: 6

解释:节点 2 和节点 8 的最近公共祖先是 6。

示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4

输出: 2

解释:节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

-tags: 算法,树

-解答:

题解

我们来复习一下二叉搜索树（BST）的性质：

1. 节点 N左子树上的所有节点的值都小于等于节点 N的值
2. 节点 N右子树上的所有节点的值都大于等于节点 N 的值
3. 左子树和右子树也都是 BST

方法一 （递归）

节点 p，q 的最近公共祖先（LCA）是距离这两个节点最近的公共祖先节点。在这里 最近 考虑的是节点的深度。

算法

1. 从根节点开始遍历树
2. 如果节点 p和节点 q 都在右子树上，那么以右孩子为根节点继续 1 的操作
3. 如果节点 p 和节点 q 都在左子树上，那么以左孩子为根节点继续 1 的操作
4. 如果条件 2 和条件 3 都不成立，这就意味着我们已经找到节 p 和节点 q 的 LCA 了

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        // Value of current node or parent node.
        int parentVal = root.val;

        // Value of p
        int pVal = p.val;

        // Value of q;
        int qVal = q.val;

        if (pVal > parentVal && qVal > parentVal) {
            // If both p and q are greater than parent
            return lowestCommonAncestor(root.right, p, q);
        } else if (pVal < parentVal && qVal < parentVal) {
            // If both p and q are lesser than parent
            return lowestCommonAncestor(root.left, p, q);
        } else {
            // We have found the split point, i.e. the LCA node.
            return root;
        }
    }
}

复杂度分析

• 时间复杂度：O(N)，在最坏的情况下我们可能需要访问 BST 中所有的节点。

• 空间复杂度：O(N)
  所需开辟的额外空间主要是递归栈产生的，而BST的高度为 N。

方法二 （迭代）

这个方法跟方法一很接近。唯一的不同是，我们用迭代的方式替代了递归来遍历整棵树。由于我们不需要回溯来找到 LCA 节点，所以我们是完全可以不利用栈或者是递归的。实际上这个问题本身就是可以迭代的，我们只需要找到分割点就可以了。这个分割点就是能让节点 p和节点 q 不能在同一颗子树上的那个节点，或者是节点 p 和节点 q 中的一个，这种情况下其中一个节点是另一个节点的父亲节点。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        // Value of p
        int pVal = p.val;

        // Value of q;
        int qVal = q.val;

        // Start from the root node of the tree
        TreeNode node = root;

        // Traverse the tree
        while (node != null) {

            // Value of ancestor/parent node.
            int parentVal = node.val;

            if (pVal > parentVal && qVal > parentVal) {
                // If both p and q are greater than parent
                node = node.right;
            } else if (pVal < parentVal && qVal < parentVal) {
                // If both p and q are lesser than parent
                node = node.left;
            } else {
                // We have found the split point, i.e. the LCA node.
                return node;
            }
        }
        return null;
    }
}

复杂度分析

• 时间复杂度：O(N)，在最坏的情况下我们可能需要遍历 BST 中所有的节点。

• 空间复杂度：O(1)

---

-问题9: Nim 游戏

你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头，每次你们轮流拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。你作为先手。

你们是聪明人，每一步都是最优解。 编写一个函数，来判断你是否可以在给定石头数量的情况下赢得游戏。

示例:
输入: 4 输出: false 解释:如果堆中有 4 块石头，那么你永远不会赢得比赛； 因为无论你拿走 1 块、2 块 还是 3 块石头，最后一块石头总是会被你的朋友拿走。

-tags: 算法,极小化极大,脑筋急转弯

-解答:
如果堆中石头的数量 n不能被 4整除，那么你总是可以赢得 Nim 游戏的胜利。

推理

让我们考虑一些小例子。显而易见的是，如果石头堆中只有一块、两块、或是三块石头，那么在你的回合，你就可以把全部石子拿走，从而在游戏中取胜。而如果就像题目描述那样，堆中恰好有四块石头，你就会失败。因为在这种情况下不管你取走多少石头，总会为你的对手留下几块，使得他可以在游戏中打败你。因此，要想获胜，在你的回合中，必须避免石头堆中的石子数为 4 的情况。

同样地，如果有五块、六块、或是七块石头，你可以控制自己拿取的石头数，总是恰好给你的对手留下四块石头，使他输掉这场比赛。但是如果石头堆里有八块石头，你就不可避免地会输掉，因为不管你从一堆石头中挑出一块、两块还是三块，你的对手都可以选择三块、两块或一块，以确保在再一次轮到你的时候，你会面对四块石头。

显然，它以相同的模式不断重复 n=4,8,12,16...，基本可以看出是 4 的倍数。

public boolean canWinNim(int n) {
    return (n % 4 != 0);
}

复杂度分析

• 时间复杂度：O(1)，只进行了一次检查。
• 空间复杂度：O(1)，没有使用额外的空间。

---

-问题10: 路径总和 III

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

返回 3。和等于 8 的路径有: 1. 5 -> 3 2. 5 -> 2 -> 1 3. -3 -> 11

-tags: 树,算法

-解答:
利用栈对二叉树进行遍历，用一个额外的数组保存所有二叉树路径的节点和，判断每个保存节点和的数组里有多少个和sum相等的数即可。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def pathSum(self, root: TreeNode, sum: int) -> int:
        if not root:
            return 0
        
        stack = [(root,[root.val])]
        res = 0

        while stack:
            node,temp = stack.pop()
            res += temp.count(sum)
            temp += [0]
            if node.left:
                arr = [i+node.left.val for i in temp]
                stack.append((node.left,arr))
            
            if node.right:
                arr = [i+node.right.val for i in temp]
                stack.append((node.right,arr))
        
        return res

---

-问题11: 找到字符串中所有字母异位词

给定一个字符串 s和一个非空字符串 p，找到 s中所有是 p的字母异位词的子串，返回这些子串的起始索引。

字符串只包含小写英文字母，并且字符串 s和 p的长度都不超过 20100。

说明：

• 字母异位词指字母相同，但排列不同的字符串。
• 不考虑答案输出的顺序。

示例 1:

输入: s: "cbaebabacd" p: "abc" 输出: [0, 6]

解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。

示例 2:

输入: s: "abab" p: "ab" 输出: [0, 1, 2]

解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的字母异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的字母异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的字母异位词。

-tags: 算法,哈希表

-解答:

滑动窗口

思路

1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。

2、我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

那么，如何判断 window 即子串 s[left...right] 是否符合要求，是否包含 t 的所有字符呢？

可以用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数，用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数，如果 window 包含所有 needs 中的键，且这些键对应的值都大于等于 needs 中的值，那么就可以知道当前「窗口」符合要求了，可以开始移动 left 指针了。

string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;

// 相当于两个计数器
unordered_map window;
unordered_map needs;
for (char c : t) needs[c]++;

// 记录 window 中已经有多少字符符合要求了
int match = 0; 

while (right < s.size()) {
    char c1 = s[right];
    if (needs.count(c1)) {
        window[c1]++; // 加入 window
        if (window[c1] == needs[c1])
            // 字符 c1 的出现次数符合要求了
            match++;
    }
    right++;

    // window 中的字符串已符合 needs 的要求了
    while (match == needs.size()) {
        // 更新结果 res
        res = minLen(res, window);
        char c2 = s[left];
        if (needs.count(c2)) {
            window[c2]--; // 移出 window
            if (window[c2] < needs[c2])
                // 字符 c2 出现次数不再符合要求
                match--;
        }
        left++;
    }
}
return res;

这个算法的时间复杂度是 O(M + N)，M 和 N 分别是字符串 S 和 T 的长度。因为我们先用 for 循环遍历了字符串 T 来初始化 needs，时间 O(N)，之后的两个 while 循环最多执行 2M 次，时间 O(M)。

读者也许认为嵌套的 while 循环复杂度应该是平方级，但是你这样想，while 执行的次数就是双指针 left 和 right 走的总路程，最多是 2M 嘛。

具体应用到这道题上：

vector findAnagrams(string s, string t) {
    // 用数组记录答案
    vector res;
    int left = 0, right = 0;
    unordered_map needs;
    unordered_map window;
    for (char c : t) needs[c]++;
    int match = 0;
    
    while (right < s.size()) {
        char c1 = s[right];
        if (needs.count(c1)) {
            window[c1]++;
            if (window[c1] == needs[c1])
                match++;
        }
        right++;

        while (match == needs.size()) {
            // 如果 window 的大小合适
            // 就把起始索引 left 加入结果
            if (right - left == t.size()) {
                res.push_back(left);
            }
            char c2 = s[left];
            if (needs.count(c2)) {
                window[c2]--;
                if (window[c2] < needs[c2])
                    match--;
            }
            left++;
        }
    }
    return res;
}

---

-问题12: 找到所有数组中消失的数字

给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。

找到所有在 [1, n] 范围之间没有出现在数组中的数字。

您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:
输入: [4,3,2,7,8,2,3,1] 输出: [5,6]

-tags: 算法,数组

-解答:
关键是用好条件： 1 ≤ a[i] ≤ n （n为数组长度） 。

a[1]-1在[0,n-1]中。将a[i]放在位置a[i]-1是可行的。

遍历元素时，当 a[i] != i+1的，就将其交换到正确的位置a[i]-1。

此时，当 a[i] == a[a[i]-1]时，表示a[i]有重复。

遍历完后，再遍历一次。所有 a[i] != i+1 的i+1就是结果。

i=0;
while(i < n){
    while(i < n 且 a[i] != i+1){
        if(a[i] == a[a[i]-1]){
            ++i;
            下一个;
        }
        交换a[i],a[a[i]-1];
    }
}
i=0;
while(i < n){
    if(a[i] == a[a[i]-1]){
        i+1是结果;
    }
    ++i;
}

代码:

    vector findDisappearedNumbers(vector& nums) {
        vector ans;
        int i=0;
        while(i < nums.size()){
            while(i < nums.size() && nums[i] != i+1){
                if(nums[i] == nums[nums[i]-1]){
                    i++;
                    continue;
                }
                swap(nums[i],nums[nums[i]-1]);
            }
            ++i;
        }
        i=0;
        while(i < nums.size()){
            if(nums[i] != i+1){
                ans.push_back(i+1);
            }        
            ++i;
        }
        
        return ans;
    }

---

-问题13: 最小移动次数使数组元素相等

给定一个长度为 n 的非空整数数组，找到让数组所有元素相等的最小移动次数。每次移动可以使 n - 1 个元素增加 1。

示例:
输入: [1,2,3] 输出: 3 解释: 只需要3次移动（注意每次移动会增加两个元素的值）： [1,2,3] => [2,3,3] => [3,4,3] => [4,4,4]

-tags: 数学,算法

-解答:

利用排序

算法

如果对数组进行排序得到有序数列 a，可以有效地简化问题。类似于方法二，我们用 diff=max-min 更新数列。但不同的是，我们不需要每次都遍历整个数组来得到最大和最小值，而是可以利用数组的有序性在 O(1) 时间内找到更新后的最大值和最小值。此外，我们也不需要真的更新数组的值。

为了便于理解，下面逐步讲解该算法。

首先，假设我们在每一步计算 diff 之后正在更新有序数组的元素。下面展示如何在不遍历数组的情况下找到最大最小值。在第一步中，最后的元素即为最大值，因此 diff=a[n-1]-a[0]。我们对除了最后一个元素以外所有元素增加 diff。

现在，更新后的数组开头元素 a'[0] 变成了 a[0]+diff=a[n-1]。因此，a'[0] 等于上一步中最大的元素 a[n-1]。由于数组排过序，直到 i-2 的元素都满足 a[j]>=a[j-1]。因此，更新之后，a'[n-2] 即为最大元素。而 a[0] 依然是最小元素。

于是，在第二次更新时，diff=a[n-2]-a[0]。更新后 a''[0] 会成为 a'[n-2]，与上一次迭代类似。

然后，由于 a'[0] 和 a'[n-1] 相等，在第二次更新后，a''[0]=a''[n-1]=a'[n-2]。于是，最大的元素为 a[n-3]。

于是，我们可以继续这样，在每一步用最大最小值差更新数组。

下面进入第二步。第一步中，我们假设每一步会更新数组 a 中的元素。但事实上，我们不需要这么做。这是因为，即使是在更新元素之后，我们要登记的 diff 差值也不变，因为 max 和 min 增加的数字相同。

于是，我们可以简单的将数组排序一次， moves=sum_{i=1}^{n-1} (a[i]-a[0])。

public class Solution {
    public int minMoves(int[] nums) {
        Arrays.sort(nums);
        int count = 0;
        for (int i = nums.length - 1; i > 0; i--) {
            count += nums[i] - nums[0];
        }
        return count;
    }
}

复杂度分析

• 时间复杂度：O(n log(n) )。 排序需要 的时间。

• 空间复杂度：O(1)。不需要额外空间。

---

动态规划

算法

如果对数组进行排序得到有序数列 a，可以有效地简化问题。考虑有序数组 a，我们不考虑整个问题，而是将问题分解。假设，**直到 i-1位置的元素都已经相等，我们只需要考虑 i 位的元素，将差值 diff=a[i]-a[i-1] 加到总移动次数上**，使得第i` 位也相等。

moves=moves+diff。

但当我们想要继续这一步时，a[i] 之后的元素也会被增加 diff，亦即 a[j]=a[j]+diff，其中 j>i。

但当实现本方法时，我们不需要对这样的 a[j] 进行增加。相反，我们把 moves 的数量增加到当前元素（a[i]）中，a'[i]=a[i]+moves。

简而言之，我们对数列进行排序，一直更新 moves 以使得直到当前的元素相等，而不改变除了当前元素之外的元素。在整个数组扫描完毕后，moves 即为答案。

public class Solution {
    public int minMoves(int[] nums) {
        Arrays.sort(nums);
        int moves = 0;
        for (int i = 1; i < nums.length; i++) {
            int diff = (moves + nums[i]) - nums[i - 1];
            nums[i] += moves;
            moves += diff;
        }
        return moves;
    }
}

复杂度分析

• 时间复杂度：O(n log(n) )。 排序需要 的时间。

• 空间复杂度：O(1)。只使用了一个变量。

---

数学法

算法

该方法基于以下思路：将除了一个元素之外的全部元素+1，等价于将该元素-1，因为我们只对元素的相对大小感兴趣。因此，该问题简化为需要进行的减法次数。

显然，我们只需要将所有的数都减到最小的数即可。为了找到答案，我们不需要真的操作这些元素。

public class Solution {
    public int minMoves(int[] nums) {
        int moves = 0, min = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            moves += nums[i];
            min = Math.min(min, nums[i]);
        }
        return moves - min * nums.length;
    }
}

复杂度分析

• 时间复杂度：O(n)。对数组进行了一次遍历。

• 空间复杂度：O(1)。不需要额外空间。

---

改进的数学法

算法

上一个方法可能存在整数越界，改进如下。

public class Solution {
    public int minMoves(int[] nums) {
        int moves = 0, min = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            min = Math.min(min, nums[i]);
        }
        for (int i = 0; i < nums.length; i++) {
            moves += nums[i] - min;
        }
        return moves;
    }
}

复杂度分析

• 时间复杂度：O(n)。一次遍历寻找最小值，一次遍历计算次数。

• 空间复杂度：O(1)。不需要额外空间。

---

-问题14: 重复的子字符串

给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过10000。

示例 1:
输入: "abab" 输出: True 解释: 可由子字符串 "ab" 重复两次构成。
示例 2:
输入: "aba" 输出: False
示例 3:
输入: "abcabcabcabc" 输出: True 解释: 可由子字符串 "abc" 重复四次构成。 (或者子字符串 "abcabc" 重复两次构成。)

-tags: 算法,字符串

-解答:
1.将原字符串给出拷贝一遍组成新字符串；
2.掐头去尾留中间；
3.如果还包含原字符串，则满足题意。

public boolean repeatedSubstringPattern(String s) {
\t\t
\tString str = s + s;
\treturn str.substring(1, str.length() - 1).contains(s);;
\t}

---

-问题15: 最大回文数乘积

你需要找到由两个 n 位数的乘积组成的最大回文数。

由于结果会很大，你只需返回最大回文数 mod 1337得到的结果。

示例:

输入: 2

输出: 987

解释: 99 x 91 = 9009, 9009 % 1337 = 987

说明:

n 的取值范围为 [1,8]。

-tags: 算法

-解答:

object Solution {
    def largestPalindrome(n: Int): Int = {
         Array(9, 987, 123, 597, 677, 1218, 877, 475)(n-1)
    }
}

---

-问题16: 下一个更大元素 I

给定两个没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x大的元素。如果不存在，对应位置输出-1。

示例 1:

输入: nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出: [-1,3,-1]

解释: 对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。 对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。 对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。

示例 2:

输入: nums1 = [2,4], nums2 = [1,2,3,4]. 输出: [3,-1]

解释: 对于num1中的数字2，第二个数组中的下一个较大数字是3。 对于num1中的数字4，第二个数组中没有下一个更大的数字，因此输出 -1。

注意:

2. nums1和nums2中所有元素是唯一的。
3. nums1和nums2 的数组大小都不超过1000。

-tags: 算法,栈

-解答:

方法一：单调栈

我们可以忽略数组 nums1，先对将 nums2 中的每一个元素，求出其下一个更大的元素。随后对于将这些答案放入哈希映射（HashMap）中，再遍历数组 nums1，并直接找出答案。对于 nums2，我们可以使用单调栈来解决这个问题。

我们首先把第一个元素 nums2[1] 放入栈，随后对于第二个元素 nums2[2]，

• 如果 nums2[2] > nums2[1]，那么我们就找到了nums2[1] 的下一个更大元素 nums2[2]，此时就可以把 nums2[1] 出栈并把 nums2[2] 入栈；
• 如果 nums2[2] <= nums2[1]，我们就仅把 nums2[2] 入栈。对于第三个元素 nums2[3]，此时栈中有若干个元素，那么所有比nums2[3]小的元素都找到了下一个更大元素（即 nums2[3]），因此可以出栈，在这之后，我们将 nums2[3] 入栈，以此类推。

可以发现，我们维护了一个单调栈，栈中的元素从栈顶到栈底是单调不降的。当我们遇到一个新的元素 nums2[i] 时，我们判断栈顶元素是否小于 nums2[i]，如果是，那么栈顶元素的下一个更大元素即为 nums2[i]，我们将栈顶元素出栈。重复这一操作，直到栈为空或者栈顶元素大于 nums2[i]。此时我们将 nums2[i] 入栈，保持栈的单调性，并对接下来的 nums2[i + 1], nums2[i + 2] ... 执行同样的操作。

public class Solution {
    public int[] nextGreaterElement(int[] findNums, int[] nums) {
        Stack < Integer > stack = new Stack < > ();
        HashMap < Integer, Integer > map = new HashMap < > ();
        int[] res = new int[findNums.length];
        for (int i = 0; i < nums.length; i++) {
            while (!stack.empty() && nums[i] > stack.peek())
                map.put(stack.pop(), nums[i]);
            stack.push(nums[i]);
        }
        while (!stack.empty())
            map.put(stack.pop(), -1);
        for (int i = 0; i < findNums.length; i++) {
            res[i] = map.get(findNums[i]);
        }
        return res;
    }
}

复杂度分析

• 时间复杂度：O(M+N)，其中 M 和 N 分别是数组 nums1 和 nums2 的长度。

• 空间复杂度：O(N)。我们在遍历 nums2 时，需要使用栈，以及哈希映射用来临时存储答案。

---

-问题17: 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。

示例 :
给定二叉树
1 / \ 2 3 / \ 4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

-tags: 树,算法

-解答:

方法 1：深度优先搜索

任意一条路径可以被写成两个 箭头（不同方向），每个箭头代表一条从某些点向下遍历到孩子节点的路径。

假设我们知道对于每个节点最长箭头距离分别为 L, R，那么最优路径经过 L + R + 1 个节点。

算法

按照常用方法计算一个节点的深度：

max(depth of node.left, depth of node.right) + 1。

在计算的同时，经过这个节点的路径长度为 1 + (depth of node.left) + (depth of node.right) 。搜索每个节点并记录这些路径经过的点数最大值，期望长度是结果 - 1。

class Solution(object):
    def diameterOfBinaryTree(self, root):
        self.ans = 1
        def depth(node):
            if not node: return 0
            L = depth(node.left)
            R = depth(node.right)
            self.ans = max(self.ans, L+R+1)
            return max(L, R) + 1

        depth(root)
        return self.ans - 1

复杂度分析

• 时间复杂度：O(N)，每个节点只访问一次。
• 空间复杂度：O(N)，深度优先搜索的栈开销。

---

-问题18: 最短无序连续子数组

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

示例 1:
输入: [2, 6, 4, 8, 10, 9, 15] 输出: 5 解释: 你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。
说明 :

2. 输入的数组长度范围在 [1, 10,000]。
3. 输入的数组可能包含重复元素 ，所以升序的意思是<=。

-tags: 算法,数组

-解答:

方法 1：暴力

算法

在暴力方法中，我们考虑 nums 数组中每一个可能的子序列。对于每一个子序列 nums[i:j] ，我们检查它是否是最小的无序子序列。因此对于每一个子序列，我们求出这个子序列中的最大和最小值，并分别用 max 和 min 表示。

如果子序列 nums[0:i-1] 和 nums[j:n-1] 是升序的，那么仅有 nums[i:j] 是可能的子序列。更进一步， nums[0:i-1] 中所有的元素都要比 min 小且 nums[j:n-1] 中所有的元素都要比 max 大。我们对于枚举的每一对 i 和 j 都做这样的检查。

接下来，我们需要检查 nums[0:i-1] 和 nums[j:n-1] 是否是升序的。如果上述所有条件都满足，我们通过枚举所有的 i 和 j 并计算 j-i 来找到最短的无序子数组。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int res = nums.length;
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j <= nums.length; j++) {
                int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE, prev = Integer.MIN_VALUE;
                for (int k = i; k < j; k++) {
                    min = Math.min(min, nums[k]);
                    max = Math.max(max, nums[k]);
                }
                if ((i > 0 && nums[i - 1] > min) || (j < nums.length && nums[j] < max))
                    continue;
                int k = 0;
                while (k < i && prev <= nums[k]) {
                    prev = nums[k];
                    k++;
                }
                if (k != i)
                    continue;
                k = j;
                while (k < nums.length && prev <= nums[k]) {
                    prev = nums[k];
                    k++;
                }
                if (k == nums.length) {
                    res = Math.min(res, j - i);

                }
            }
        }
        return res;
    }
}

复杂度分析

• 时间复杂度：O(n^3) 。使用了三重循环。

• 空间复杂度：O(1) 。只使用了常数空间。

方法 2：更好的暴力

算法

在这种方法中，我们基于选择排序使用如下想法：我们遍历 nums 数组中的每一个元素 nums[i] 。对于每一个元素，我们尝试找到它在正确顺序数组中的位置，即将它与每一个满足 i < j < n 的 nums[j] 做比较，这里 n 是 nums 数组的长度。

如果存在 nums[j] 比 nums[i] 小，这意味着 nums[i] 和 nums[j] 都不在排序后数组中的正确位置。因此我们需要交换这两个元素使它们到正确的位置上。但这里我们并不需要真的交换两个元素，我们只需要标记两个元素在原数组中的位置 i 和 j 。这两个元素标记着目前无序数组的边界。

因此，在所有的 nums[i] 中，我们找到最左边不在正确位置的 nums[i] ，这标记了最短无序子数组的左边界（l）。类似的，我们找到最右边不在正确位置的边界 nums[j] ，它标记了最短无序子数组的右边界 (r) 。

因此，我们可以求得最短无序子数组的长度为 r - l + 1 。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int l = nums.length, r = 0;
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] < nums[i]) {
                    r = Math.max(r, j);
                    l = Math.min(l, i);
                }
            }
        }
        return r - l < 0 ? 0 : r - l + 1;
    }
}

复杂度分析

• 时间复杂度：O(n^2) 。使用了两重循环。

• 空间复杂度：O(1) 。只使用了常数空间。

方法 3：排序

算法

另一个简单的想法是：我们将数组 nums 进行排序，记为 nums_sorted 。然后我们比较 nums 和 nums_sorted 的元素来决定最左边和最右边不匹配的元素。它们之间的子数组就是要求的最短无序子数组。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] snums = nums.clone();
        Arrays.sort(snums);
        int start = snums.length, end = 0;
        for (int i = 0; i < snums.length; i++) {
            if (snums[i] != nums[i]) {
                start = Math.min(start, i);
                end = Math.max(end, i);
            }
        }
        return (end - start >= 0 ? end - start + 1 : 0);
    }
}

复杂度分析

• 时间复杂度：O(n log n) 。排序消耗 n log n 的时间。

• 空间复杂度：O(n) 。我们拷贝了一份原数组来进行排序。

方法 4：使用栈

算法

这个方法背后的想法仍然是选择排序。我们需要找到无序子数组中最小元素和最大元素分别对应的正确位置，来求得我们想要的无序子数组的边界。

为了达到这一目的，此方法中，我们使用 栈 。我们从头遍历 nums 数组，如果遇到的数字大小一直是升序的，我们就不断把对应的下标压入栈中，这么做的目的是因为这些元素在目前都是处于正确的位置上。一旦我们遇到前面的数比后面的数大，也就是 nums[j] 比栈顶元素小，我们可以知道 nums[j] 一定不在正确的位置上。

为了找到 nums[j] 的正确位置，我们不断将栈顶元素弹出，直到栈顶元素比 nums[j] 小，我们假设栈顶元素对应的下标为 k ，那么我们知道 nums[j] 的正确位置下标应该是 k + 1 。

我们重复这一过程并遍历完整个数组，这样我们可以找到最小的 k， 它也是无序子数组的左边界。

类似的，我们逆序遍历一遍 nums 数组来找到无序子数组的右边界。这一次我们将降序的元素压入栈中，如果遇到一个升序的元素，我们像上面所述的方法一样不断将栈顶元素弹出，直到找到一个更大的元素，以此找到无序子数组的右边界。

我们可以看下图作为参考。我们观察到上升还是下降决定了相对顺序，我们还可以观察到指针 b 在下标 0 后面标记着无序子数组的左边界，指针 a 在下标 7 前面标记着无序子数组的右边界。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        Stack < Integer > stack = new Stack < Integer > ();
        int l = nums.length, r = 0;
        for (int i = 0; i < nums.length; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] > nums[i])
                l = Math.min(l, stack.pop());
            stack.push(i);
        }
        stack.clear();
        for (int i = nums.length - 1; i >= 0; i--) {
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i])
                r = Math.max(r, stack.pop());
            stack.push(i);
        }
        return r - l > 0 ? r - l + 1 : 0;
    }
}

复杂度分析

• 时间复杂度：O(n)。需要遍历数组一遍，栈的时间复杂度也为 O(n)。

• 空间复杂度：O(n)。栈的大小最大达到 n。

方法 5：不使用额外空间

算法

这个算法背后的思想是无序子数组中最小元素的正确位置可以决定左边界，最大元素的正确位置可以决定右边界。

因此，首先我们需要找到原数组在哪个位置开始不是升序的。我们从头开始遍历数组，一旦遇到降序的元素，我们记录最小元素为 min 。

类似的，我们逆序扫描数组 nums，当数组出现升序的时候，我们记录最大元素为 max。

然后，我们再次遍历 nums 数组并通过与其他元素进行比较，来找到 min 和 max 在原数组中的正确位置。我们只需要从头开始找到第一个大于 min 的元素，从尾开始找到第一个小于 max 的元素，它们之间就是最短无序子数组。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        boolean flag = false;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] < nums[i - 1])
                flag = true;
            if (flag)
                min = Math.min(min, nums[i]);
        }
        flag = false;
        for (int i = nums.length - 2; i >= 0; i--) {
            if (nums[i] > nums[i + 1])
                flag = true;
            if (flag)
                max = Math.max(max, nums[i]);
        }
        int l, r;
        for (l = 0; l < nums.length; l++) {
            if (min < nums[l])
                break;
        }
        for (r = nums.length - 1; r >= 0; r--) {
            if (max > nums[r])
                break;
        }
        return r - l < 0 ? 0 : r - l + 1;
    }
}

复杂度分析

• 时间复杂度：O(n)。使用了4个 O(n) 的循环。

• 空间复杂度：O(1)。使用了常数空间。

---

-问题19: 两数之和 IV - 输入 BST

给定一个二叉搜索树和一个目标结果，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

案例 1:
输入: 5 / \ 3 6 / \ \ 2 4 7 Target = 9 输出: True
案例 2:
输入: 5 / \ 3 6 / \ \ 2 4 7 Target = 28 输出: False

-tags: 树,算法

-解答:

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def findTarget(self, root: TreeNode, k: int) -> bool:
        def inorder(root):
            if not root:
                return []
            return inorder(root.left)+[root.val]+inorder(root.right)
        numbers = sorted(inorder(root))
        n = len(numbers)
           
        i = 0
        j = n-1
        while i < j:
             if numbers[i] + numbers[j] > k:
                j -= 1
             elif numbers[i] + numbers[j] < k:
                i +=1
             else:
                return True
        return False

---

-问题20: 最长同值路径

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

注意：两个节点之间的路径长度由它们之间的边数表示。

示例 1:

输入:
5 / \ 4 5 / \ \ 1 1 5
输出:
2
示例 2:

输入:
1 / \ 4 5 / \ \ 4 4 5
输出:
2
注意: 给定的二叉树不超过10000个结点。 树的高度不超过1000。

-tags: 树,递归,算法

-解答:

方法：递归

思路

我们可以将任何路径（具有相同值的节点）看作是最多两个从其根延伸出的箭头。

具体地说，路径的根将是唯一节点，因此该节点的父节点不会出现在该路径中，而箭头将是根在该路径中只有一个子节点的路径。

然后，对于每个节点，我们想知道向左延伸的最长箭头和向右延伸的最长箭头是什么？我们可以用递归来解决这个问题。

算法

令 arrow_length(node) 为从节点 node 延伸出的最长箭头的长度。如果 node.Left 存在且与节点 node 具有相同的值，则该值就会是 1 + arrow_length(node.left)。在 node.right 存在的情况下也是一样。

当我们计算箭头长度时，候选答案将是该节点在两个方向上的箭头之和。我们将这些候选答案记录下来，并返回最佳答案。

class Solution {
    int ans;
    public int longestUnivaluePath(TreeNode root) {
        ans = 0;
        arrowLength(root);
        return ans;
    }
    public int arrowLength(TreeNode node) {
        if (node == null) return 0;
        int left = arrowLength(node.left);
        int right = arrowLength(node.right);
        int arrowLeft = 0, arrowRight = 0;
        if (node.left != null && node.left.val == node.val) {
            arrowLeft += left + 1;
        }
        if (node.right != null && node.right.val == node.val) {
            arrowRight += right + 1;
        }
        ans = Math.max(ans, arrowLeft + arrowRight);
        return Math.max(arrowLeft, arrowRight);
    }
}

复杂度分析

• 时间复杂度：O(N)，其中 N 是树中节点数。我们处理每个节点一次。

• 空间复杂度：O(H)，其中 H 是树的高度。我们的递归调用栈可以达到 H 层的深度。

---

-问题21: 计数二进制子串

给定一个字符串 s，计算具有相同数量0和1的非空(连续)子字符串的数量，并且这些子字符串中的所有0和所有1都是组合在一起的。

重复出现的子串要计算它们出现的次数。

示例 1 :
输入: "00110011" 输出: 6 解释: 有6个子串具有相同数量的连续1和0：“0011”，“01”，“1100”，“10”，“0011” 和 “01”。 请注意，一些重复出现的子串要计算它们出现的次数。 另外，“00110011”不是有效的子串，因为所有的0（和1）没有组合在一起。
示例 2 :
输入: "10101" 输出: 4 解释: 有4个子串：“10”，“01”，“10”，“01”，它们具有相同数量的连续1和0。
注意：

• s.length 在1到50,000之间。
• s 只包含“0”或“1”字符。

-tags: 算法,字符串

-解答:

方法一：按字符分组

我们可以将字符串 s 转换为 groups 数组表示字符串中相同字符连续块的长度。例如，如果 s=“11000111000000”，则 groups=[2，3，4，6]。

对于 '0' * k + '1' * k 或 '1' * k + '0' * k 形式的每个二进制字符串，此字符串的中间部分必须出现在两个组之间。

让我们尝试计算 groups[i] 和 groups[i+1] 之间的有效二进制字符串数。如果我们有 groups[i] = 2, groups[i+1] = 3，那么它表示 “00111” 或 “11000”。显然，我们可以在此字符串中生成 min(groups[i], groups[i+1]) 有效的二进制字符串。

算法：

• 让我们创建上面定义的 groups。s 的第一个元素属于它自己的组。每个元素要么与前一个元素不匹配，从而开始一个大小为 1 的新组；要么匹配，从而使最近一个组的大小增加 1。
• 然后，我们将取 min(groups[i-1], groups[i]) 的和。

class Solution(object):
    def countBinarySubstrings(self, s):
        groups = [1]
        for i in xrange(1, len(s)):
            if s[i-1] != s[i]:
                groups.append(1)
            else:
                groups[-1] += 1

        ans = 0
        for i in xrange(1, len(groups)):
            ans += min(groups[i-1], groups[i])
        return ans

复杂度分析

• 时间复杂度：O(N)。其中 N 是 s 的长度。每个循环都是 O(N)。
• 空间复杂度：O(N)，groups 使用的空间。

方法二：线性扫描

我们可以修改我们的方法 1 来实时计算答案。我们将只记住 prev = groups[-2] 和 cur=groups[-1] 来代替 groups。然后，答案是我们看到的每个不同的 (prev, cur) 的 min(prev, cur) 之和。

class Solution(object):
    def countBinarySubstrings(self, s):
        ans, prev, cur = 0, 0, 1
        for i in xrange(1, len(s)):
            if s[i-1] != s[i]:
                ans += min(prev, cur)
                prev, cur = cur, 1
            else:
                cur += 1

        return ans + min(prev, cur)

复杂度分析

• 时间复杂度：O(N)。其中 N 是 s 的长度。每个循环都是 O(N)。
• 空间复杂度：O(1)。

---

-问题22: 1比特与2比特字符

有两种特殊字符。第一种字符可以用一比特0来表示。第二种字符可以用两比特(10 或 11)来表示。

现给一个由若干比特组成的字符串。问最后一个字符是否必定为一个一比特字符。给定的字符串总是由0结束。

示例 1:
输入: bits = [1, 0, 0] 输出: True 解释: 唯一的编码方式是一个两比特字符和一个一比特字符。所以最后一个字符是一比特字符。
示例 2:
输入: bits = [1, 1, 1, 0] 输出: False 解释: 唯一的编码方式是两比特字符和两比特字符。所以最后一个字符不是一比特字符。
注意:

• 1 <= len(bits) <= 1000.
• bits[i] 总是0 或 1.

-tags: 算法,数组

-解答:

方法一：线性扫描

我们可以对 bits 数组从左到右扫描来判断最后一位是否为一比特字符。当扫描到第 i 位时，如果 bits[i]=1，那么说明这是一个两比特字符，将 i 的值增加 2。如果 bits[i]=0，那么说明这是一个一比特字符，将 i 的值增加 1。

如果 i 最终落在了 bits[length-1] 的位置，那么说明最后一位一定是一比特字符。

class Solution(object):
    def isOneBitCharacter(self, bits):
        i = 0
        while i < len(bits) - 1:
            i += bits[i] + 1
        return i == len(bits) - 1

复杂度分析

• 时间复杂度：O(n)，其中 n 是 bits 数组的长度。
• 空间复杂度：O(1)。

方法二：贪心

三种字符分别为 0，10 和 11，那么 bits 数组中出现的所有 0 都表示一个字符的结束位置（无论其为一比特还是两比特）。因此最后一位是否为一比特字符，只和他左侧出现的连续的 1 的个数（即它与倒数第二个 0 出现的位置之间的 1 的个数，如果bits数组中只有 1 个 0，那么就是整个数组的长度减一）有关。如果 1 的个数为偶数个，那么最后一位是一比特字符，如果 1 的个数为奇数个，那么最后一位不是一比特字符。

class Solution(object):
    def isOneBitCharacter(self, bits):
        parity = bits.pop()
        while bits and bits.pop(): parity ^= 1
        return parity == 0

复杂度分析

• 时间复杂度：O(n)，其中 N 是 bits 数组的长度。
• 空间复杂度：O(1)。

---

-问题23: 词典中最长的单词

给出一个字符串数组words组成的一本英语词典。从中找出最长的一个单词，该单词是由words词典中其他单词逐步添加一个字母组成。若其中有多个可行的答案，则返回答案中字典序最小的单词。

若无答案，则返回空字符串。

示例 1:

输入: words = ["w","wo","wor","worl", "world"] 输出: "world"

解释: 单词"world"可由"w", "wo", "wor", 和 "worl"添加一个字母组成。

示例 2:

输入: words = ["a", "banana", "app", "appl", "ap", "apply", "apple"] 输出: "apple"

解释: "apply"和"apple"都能由词典中的单词组成。但是"apple"得字典序小于"apply"。

注意:

• 所有输入的字符串都只包含小写字母。
• words数组长度范围为[1,1000]。
  -words[i]的长度范围为[1,30]。

-tags: 算法,字典树,哈希表

-解答:

方法一：暴力法

对于每个单词，我们可以检查它的全部前缀是否存在，可以通过 Set 数据结构来加快查找

算法：

• 当我们找到一个单词它的长度更长且它的全部前缀都存在，我们将更改答案。
• 或者，我们可以事先将单词排序，这样当我们找到一个符合条件的单词就可以认定它是答案。

class Solution(object):
    def longestWord(self, words):
    ans = ""
    wordset = set(words)
    for word in words:
        if len(word) > len(ans) or len(word) == len(ans) and word < ans:
            if all(word[:k] in wordset for k in xrange(1, len(word))):
                ans = word

    return ans

复杂度分析

• 时间复杂度：O(sum w_i^2)。w_i 指的是 words[i] 的长度，在 Set 中检查 words[i] 全部前缀是否均存在的时间复杂度是 O(sum w_i^2)。
• 空间复杂度：O(sum w_i^2) 用来存放子串的空间。

方法二：前缀树 + 深度优先搜索

由于涉及到字符串的前缀，通常可以使用 trie（前缀树）来解决。

算法：

• 将所有单词插入 trie，然后从 trie 进行深度优先搜索，每找到一个单词表示该单词的全部前缀均存在，我们选取长度最长的单词。
• 在 python 中，我们使用了 defaultdict 的方法。而在 java 中，我们使用了更通用的面向对象方法。

class Solution(object):
    def longestWord(self, words):
        Trie = lambda: collections.defaultdict(Trie)
        trie = Trie()
        END = True

        for i, word in enumerate(words):
            reduce(dict.__getitem__, word, trie)[END] = i

        stack = trie.values()
        ans = ""
        while stack:
            cur = stack.pop()
            if END in cur:
                word = words[cur[END]]
                if len(word) > len(ans) or len(word) == len(ans) and word < ans:
                    ans = word
                stack.extend([cur[letter] for letter in cur if letter != END])

        return ans

复杂度分析

• 时间复杂度：O(sum w_i)。w_i 指的是 words[i] 的长度。该时间复杂度用于创建前缀树和查找单词。

如果我们使用一个 BFS 代替 DFS，并在数组中对子节点进行排序，我们就可以不必检查每个节点上的候选词是否比答案好，最佳答案将是最后访问的节点。

• 空间复杂度：O(sum w_i)，前缀树所使用的空间。

---

-问题24: 寻找比目标字母大的最小字母

给定一个只包含小写字母的有序数组letters 和一个目标字母 target，寻找有序数组里面比目标字母大的最小字母。

数组里字母的顺序是循环的。举个例子，如果目标字母target = 'z' 并且有序数组为 letters = ['a', 'b']，则答案返回 'a'。

示例:

输入: letters = ["c", "f", "j"] target = "a" 输出: "c"

输入: letters = ["c", "f", "j"] target = "c" 输出: "f"

输入: letters = ["c", "f", "j"] target = "d" 输出: "f"

输入: letters = ["c", "f", "j"] target = "g" 输出: "j"

输入: letters = ["c", "f", "j"] target = "j" 输出: "c"

输入: letters = ["c", "f", "j"] target = "k" 输出: "c"

注:

2. letters长度范围在[2, 10000]区间内。

3. letters 仅由小写字母组成，最少包含两个不同的字母。

4. 目标字母target 是一个小写字母。

-tags: 二分查找,算法

-解答:

方法一：记录存在的字母

算法

• 我们可以扫描 letters 记录字母是否存在。我们可以用大小为 26 的数组或者 Set 来实现。
• 然后，从下一个字母（从比目标大一个的字母开始）开始检查一下是否存在。如果有的话则是答案。

class Solution(object):
    def nextGreatestLetter(self, letters, target):
        seen = set(letters)
        for i in xrange(1, 26):
            cand = chr((ord(target) - ord('a') + i) % 26 + ord('a'))
            if cand in seen:
                return cand

复杂度分析

• 时间复杂度：O(N)。N 指的是 letters 的长度，我们扫描数组的每个元素。
• 空间复杂度：O(1)。seen 最大的空间为 26。

方法二：线性扫描

算法：
由于 letters 已经有序，当我们从左往右扫描找到比目标字母大字母则该字母就是答案。否则(letters 不为空)答案将是 letters[0]。

class Solution(object):
    def nextGreatestLetter(self, letters, target):
        for c in letters:
            if c > target:
                return c
        return letters[0]

复杂度分析

• 时间复杂度：O(N)。N 指的是 letters 的长度，我们扫描数组的每个元素。
• 空间复杂度：O(1)。只使用了指针。

方法三：二分查找

算法：

• 如方法二一样，我们想要在有序数组中查找比目标字母大的最小字母，可以使用二分查找：让我们找到最右边的位置将 target 插入 letters 中，以便它保持排序。
• 二分查找分几轮进行，在每一轮中我们保持循环始终在区间 [lo，hi]。让 mi = (lo + hi) / 2。若 letters[mi] <= target，则我们修改查找区间为 [mi + 1, hi]，否则，我们修改为 [lo, mi]
• 最后，如果插入位置是最后一个位置 letters.length，则返回 letters[0]。这就是模运算的运用。

class Solution(object):
    def nextGreatestLetter(self, letters, target):
        index = bisect.bisect(letters, target)
        return letters[index % len(letters)]

复杂度分析

• 时间复杂度：O(log N)。N 指的是 letters 的长度，我们只查看数组中的 log n个元素。
• 空间复杂度：O(1)。只使用了指针。

---

-问题25: 二叉搜索树中的众数

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

• 结点左子树中所含结点的值小于等于当前结点的值
• 结点右子树中所含结点的值大于等于当前结点的值
• 左子树和右子树都是二叉搜索树

例如：
给定 BST [1,null,2,2],
1 \ 2 / 2
返回[2].

提示：如果众数超过1个，不需考虑输出顺序

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

-tags: 树,算法

-解答:

    int maxTimes = 0;
    int thisTimes = 0;
    List res = new LinkedList();
    TreeNode pre = null;
    public int[] findMode(TreeNode root) {
        inOrder(root);
        int length = res.size();
        int[] rr = new int[length];
        for(int i = 0; i < length; i++) {
            rr[i] = res.get(i);
        } 
        return rr;
    }
    public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        if(pre != null && pre.val == root.val) {
            thisTimes++;
        } else {
            thisTimes = 1;
        }
        if(thisTimes == maxTimes) {
            res.add(root.val);
        } else if(thisTimes > maxTimes) {
            maxTimes = thisTimes;
            res.clear();
            res.add(root.val);
        }
        pre = root;
        inOrder(root.right);
    }

---

-问题26: N叉树的后序遍历

给定一个 N 叉树，返回其节点值的后序遍历。

例如，给定一个 3叉树 :

image

返回其后序遍历: [5,6,3,2,4,1].

说明: 递归法很简单，你可以使用迭代法完成此题吗?

-tags: 树,算法

-解答:
由于递归实现 N 叉树的后序遍历较为简单，因此我们只讲解如何使用迭代的方法得到 N 叉树的后序遍历。

在后序遍历中，我们会先遍历一个节点的所有子节点，再遍历这个节点本身。例如当前的节点为 u，它的子节点为 v1, v2, v3 时，那么后序遍历的结果为

[children of v1], v1, [children of v2], v2, [children of v3], v3, u，

其中 [children of vk] 表示以 vk 为根节点的子树的后序遍历结果（不包括 vk 本身）。我们将这个结果反转，可以得到

u, v3, [children of v3]', v2, [children of v2]', v1, [children of v1]'，

其中 [a]' 表示 [a] 的反转。此时我们发现，结果和前序遍历非常类似，只不过前序遍历中对子节点的遍历顺序是 v1, v2, v3，而这里是 v3, v2, v1。

因此我们可以使用和 N叉树的前序遍历 相同的方法，使用一个栈来得到后序遍历。我们首先把根节点入栈。

当每次我们从栈顶取出一个节点 u 时，就把 u 的所有子节点顺序推入栈中。例如 u 的子节点从左到右为 v1, v2, v3，那么推入栈的顺序应当为 v1, v2, v3，这样就保证了下一个遍历到的节点（即 u 的第一个子节点 v3）出现在栈顶的位置。在遍历结束之后，我们把遍历结果反转，就可以得到后序遍历。

class Solution(object):
    def postorder(self, root):
        """
        :type root: Node
        :rtype: List[int]
        """
        if root is None:
            return []
        
        stack, output = [root, ], []
        while stack:
            root = stack.pop()
            if root is not None:
                output.append(root.val)
            for c in root.children:
                stack.append(c)
                
        return output[::-1]

class Solution {
    public List postorder(Node root) {
        LinkedList stack = new LinkedList<>();
        LinkedList output = new LinkedList<>();
        if (root == null) {
            return output;
        }

      stack.add(root);
      while (!stack.isEmpty()) {
          Node node = stack.pollLast();
          output.addFirst(node.val);
          for (Node item : node.children) {
              if (item != null) {
                  stack.add(item);    
              } 
          }
      }
      return output;
    }
}

复杂度分析

• 时间复杂度：时间复杂度：O(M)，其中 M 是 N 叉树中的节点个数。每个节点只会入栈和出栈各一次。

• 空间复杂度：O(M)。在最坏的情况下，这棵 N 叉树只有2层，所有第2层的节点都是根节点的孩子。将根节点推出栈后，需要将这些节点都放入栈，共有M - 1个节点，因此栈的大小为O(M)。

---

-问题27: 比较含退格的字符串

给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。 # 代表退格字符。

示例 1：
输入：S = "ab#c", T = "ad#c" 输出：true 解释：S 和 T 都会变成 “ac”。
示例 2：
输入：S = "ab##", T = "c#d#" 输出：true 解释：S 和 T 都会变成 “”。
示例 3：
输入：S = "a##c", T = "#a#c" 输出：true 解释：S 和 T 都会变成 “c”。
示例 4：
输入：S = "a#c", T = "b" 输出：false 解释：S 会变成 “c”，但 T 仍然是 “b”。
提示：

2. 1 <= S.length <= 200
3. 1 <= T.length <= 200
4. S 和 T 只含有小写字母以及字符 '#'。

-tags: 算法,栈,双指针

-解答:

class Solution {
    public boolean backspaceCompare(String S, String T) {
        int i, j, k;
        char[] charS, charT;

        i = 0;
        j = 0;
        charS = new char[S.length()];
        charT = new char[T.length()];
        for(k = 0; k < S.length(); k++){
            if(S.charAt(k) == '#'){
                if(i > 0)
                    i--;
            }
            else
                charS[i++] = S.charAt(k);
        } 
        for(k = 0; k < T.length(); k++){
            if(T.charAt(k) == '#'){
                if(j > 0)
                    j--;
            }
            else{
                charT[j++] = T.charAt(k);
            }
        } 
        if(i != j)
            return false;
        for(k = 0; k < i; k++)
            if(charS[k] != charT[k])
                return false;
        return true;
    }
}

---

-问题28: 递增顺序查找树

给定一个树，按中序遍历重新排列树，使树中最左边的结点现在是树的根，并且每个结点没有左子结点，只有一个右子结点。

示例 ：

输入：

[5,3,6,2,4,null,8,1,null,null,null,7,9]

输出：

[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

提示：

2. 给定树中的结点数介于 1 和 100 之间。

3. 每个结点都有一个从 0 到 1000 范围内的唯一整数值。

-tags: 树,算法,深度优先搜索

-解答:

方法一：中序遍历 + 构造新的树

我们在树上进行中序遍历，就可以从小到大得到树上的节点。我们把这些节点的对应的值存放在数组中，它们已经有序。接着我们直接根据数组构件题目要求的树即可。

class Solution {    
    public TreeNode increasingBST(TreeNode root) {
        List vals = new ArrayList();
        inorder(root, vals);
        TreeNode ans = new TreeNode(0), cur = ans;
        for (int v: vals) {
            cur.right = new TreeNode(v);
            cur = cur.right;
        }
        return ans.right;
    }

    public void inorder(TreeNode node, List vals) {
        if (node == null) return;
        inorder(node.left, vals);
        vals.add(node.val);
        inorder(node.right, vals);
    }
}

class Solution:
    def increasingBST(self, root):
        def inorder(node):
            if node:
                yield from inorder(node.left)
                yield node.val
                yield from inorder(node.right)

        ans = cur = TreeNode(None)
        for v in inorder(root):
            cur.right = TreeNode(v)
            cur = cur.right
        return ans.right

复杂度分析

• 时间复杂度：O(N)，其中 N 是树上的节点个数。

• 空间复杂度：O(N)。

方法二：中序遍历 + 更改树的连接方式

和方法一类似，我们在树上进行中序遍历，但会将树中的节点之间重新连接而不使用额外的空间。具体地，当我们遍历到一个节点时，把它的左孩子设为空，并将其本身作为上一个遍历到的节点的右孩子。

class Solution {
    TreeNode cur;
    public TreeNode increasingBST(TreeNode root) {
        TreeNode ans = new TreeNode(0);
        cur = ans;
        inorder(root);
        return ans.right;
    }

    public void inorder(TreeNode node) {
        if (node == null) return;
        inorder(node.left);
        node.left = null;
        cur.right = node;
        cur = node;
        inorder(node.right);
    }
}

class Solution:
    def increasingBST(self, root):
        def inorder(node):
            if node:
                inorder(node.left)
                node.left = None
                self.cur.right = node
                self.cur = node
                inorder(node.right)

        ans = self.cur = TreeNode(None)
        inorder(root)
        return ans.right

复杂度分析

• 时间复杂度：O(N)，其中 N 是树上的节点个数。

• 空间复杂度：O(H)，其中 H 是数的高度。

---