OpenCV基于Python霍夫圆检测—标准霍夫圆检测
标准霍夫圆检测
- 1. 简介
- 2. 标准霍夫圆检测
-
- 2.1 情形一
- 2.2 情形二
- 2.3 情形三
- 3. 程序演示
- 4. 结尾
- 参考资料
1. 简介
1972年,R. D. Duda和P. E. Hart1提出了直线的检测方法,而且还推广到了霍夫圆的检测方法,通常称为标准的霍夫圆检测。
2. 标准霍夫圆检测
2.1 情形一
已知圆的圆心坐标为 ( a , b ) (a, b) (a,b),半径为 r r r,则圆在 x o y xoy xoy平面内的方程可表示为: ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2。那么反过来考虑一个简单的问题:已知 x o y xoy xoy平面内的点 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) 、 ( x 3 , y 3 ) 、 . . . (x_1, y_1)、(x_2, y_2)、(x_3, y_3)、... (x1,y1)、(x2,y2)、(x3,y3)、...,且已知这些点在一个半径为 r r r的圆上,如何求这个圆的圆心?
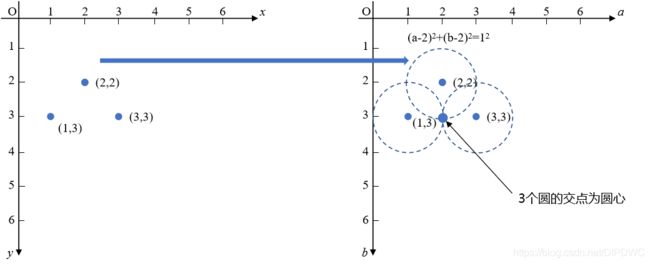
下面通过一个简单的示例来理解上述问题的求解过程。如下图1所示,假设在 x o y xoy xoy平面内有三个点 ( 1 , 3 ) 、 ( 2 , 2 ) 、 ( 3 , 3 ) (1, 3)、(2, 2)、(3, 3) (1,3)、(2,2)、(3,3),且知道这三个点在一个半径为1的圆上,可以通过中学知识尺规作图法找到圆心,以每个点为圆心、1为半径分别画圆,则这三个圆的交点及即为圆心。
现从另一个角度来理解尺规作图的过程。将 ( 1 , 3 ) (1, 3) (1,3)代入圆方程得 ( 1 − a ) 2 + ( 3 − b ) 2 = 1 2 (1-a)^2+(3-b)^2=1^2 (1−a)2+(3−b)2=12,所以可以理解为一个点对应到 a o b aob aob平面内的一个圆;同理,通过其他两个点也可以得到两个圆,那么这三个圆在 a o b aob aob平面内共同的交点即为三个点共圆的圆心。
2.2 情形二
在上面问题的基础上,提出一个稍微复杂一点的问题:已知 x o y xoy xoy平面内的点 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) 、 ( x 3 , y 3 ) 、 . . . (x_1, y_1)、(x_2, y_2)、(x_3, y_3)、... (x1,y1)、(x2,y2)、(x3,y3)、...,且已知这些点在多个圆上,这些圆的半径均为 r r r,那么哪些点在同一个圆上,并计算出圆心的坐标。
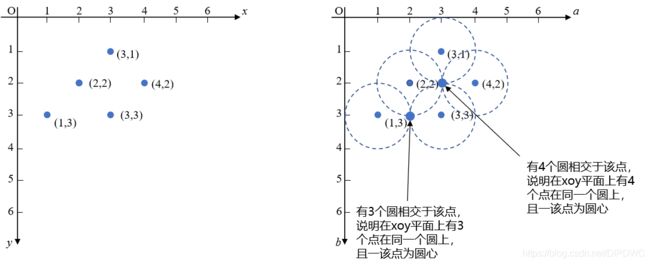
例如已知在 x o y xoy xoy平面内有5个点 ( 1 , 3 ) 、 ( 2 , 2 ) 、 ( 3 , 3 ) 、 ( 3 , 1 ) 、 ( 4 , 3 ) (1, 3)、(2, 2)、(3, 3)、(3, 1)、(4, 3) (1,3)、(2,2)、(3,3)、(3,1)、(4,3),且知道这些点可能位于不同的圆上,这些圆的半径均为1,求出哪些点在同一个圆上。这里也用尺规作图法,首先分别以5个点为圆心、1为半径作出5个圆,圆的交点即为圆心,如下图2所示。
2.3 情形三
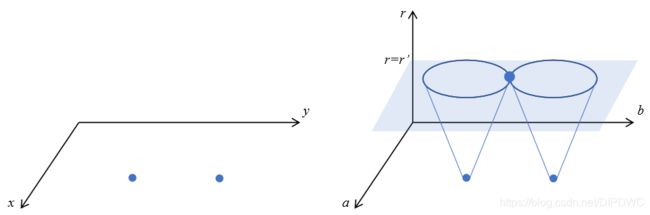
以上碰到的两种情况均是在已知半径的情况下,现引入一个更复杂的问题:已知 x o y xoy xoy平面内的点 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) 、 ( x 3 , y 3 ) 、 . . . (x_1, y_1)、(x_2, y_2)、(x_3, y_3)、... (x1,y1)、(x2,y2)、(x3,y3)、...,求出哪些点在同一个圆上且半径为多少,以及圆心的坐标。由于多了一个参数,所以需要第三维的坐标 r r r,即需要在三维空间 a b r abr abr中讨论该问题。任意一个点 ( x i , y i ) (x_i, y_i) (xi,yi)对应到 a b r abr abr空间中的锥面 ( x i − a ) 2 + ( y i − b ) 2 = r 2 (x_i-a)^2+(y_i-b)^2=r^2 (xi−a)2+(yi−b)2=r2,那么如果多个锥面相交于一点 ( a ′ , b ′ , r ′ ) (a', b', r') (a′,b′,r′),则说明这些锥面对应的 x o y xoy xoy平面内的点是共圆的且圆心为 ( a ′ , b ′ ) (a', b') (a′,b′),半径为 r ′ r' r′,如下图3所示。
该过程相当于先固定 r r r,然后转换为以上讨论的已知 r r r的情况,即第二个问题是第三个问题的一种特殊情况。
3. 程序演示
与霍夫直线检测类似,图像的霍夫圆检测就是检测哪些前景或边缘像素点在同一个圆上,并给出对应圆的圆心坐标及圆的半径;而且仍然需要计数器来完成该过程,只是这里的计数器从二维变成了三维,下面利用Python来详细描述构造三维计数器的过程,并对下图进行霍夫圆检测。
# -*- coding: utf-8 -*-
import sys
import numpy as np
import cv2
import math
# 标准霍夫圆检测
def HTCircle(I, minR, maxR, voteThresh=100):
# 宽、高
H, W = I.shape
# 归为整数
minr = round(minR) + 1
maxr = round(maxR) + 1
# 初始化三维的计数器
r_num = int(maxr - minr + 1)
a_num = int(W - 1 + maxr + maxr + 1)
b_num = int(H - 1 + maxr + maxr + 1)
accumulator = np.zeros((r_num, b_num, a_num), np.int32)
# 投票计数
for y in range(H):
for x in range(W):
if (I[y][x] == 255): # 只对边缘点做霍夫变换
for k in range(r_num): # r 变化的步长为 1
for theta in np.linspace(0, 360, 360):
# 计算对应的 a 和 b
a = x - (minr + k) * math.cos(theta / 180.0 * math.pi)
b = y - (minr + k) * math.sin(theta / 180.0 * math.pi)
# 取整
a = int(round(a))
b = int(round(b))
# 投票
accumulator[k, b, a] += 1
# 筛选投票数 大于 voteThresh的圆
circles = []
for k in range(r_num):
for b in range(b_num):
for a in range(a_num):
if (accumulator[k, b, a] > voteThresh):
circles.append((k + minr, b, a))
return circles
# 主函数
if __name__ == "__main__":
# if len(sys.argv) > 1:
# 输入图像
I = cv2.imread('../data/coins.jpg', 1)
# print(I.shape)
# canny 边缘检测
edge = cv2.Canny(I, 50, 200)
cv2.imshow("edge", edge)
cv2.waitKey()
# 霍夫圆检测
circles = HTCircle(edge, 30, 60, 80)
# 画圆
for i in range(len(circles)):
cv2.circle(I, (int(circles[i][2]), int(circles[i][1])), int(circles[i][0]), (0, 0, 255), 2)
# 绘制圆心
cv2.circle(I, (int(circles[i][2]), int(circles[i][1])), 2, (0, 0, 255), 3)
cv2.imshow("detected circles", I)
cv2.waitKey(0)
cv2.destroyAllWindows()
上述代码单纯从原理出发进行描述构造三维计数器的过程,目的是加深对标准霍夫圆检测原理的理解。由于其计算量较大运行效率较低,下一讲基于梯度霍夫圆检测函数HoughCircles将会在这些方面有较大的改进。
4. 结尾
在这一讲中,我们对标准霍夫圆检测由浅入深地分三种情形进行了讨论,从检测原理的角度出发给出了程序演示代码,描述构造三维计数器的过程,在下一讲将讲解基于梯度的霍夫圆检测函数。
参考资料
- 《OpenCV算法精解:基于Python和C++》(张平 编著),电子工业出版社,2017
- Duda R O , Hart P E . Use of the Hough Transform to Detect Lines and Curves in Pictures. 1975.
![]()
Duda R O , Hart P E . Use of the Hough Transform to Detect Lines and Curves in Pictures. 1975. ↩︎