最新的学习笔记—《信息安全数学基础》

《信息安全数学基础》最新学习笔记（BUAA本科生教材）

摘要

这里是关于《信息安全数学基础》书的个人笔记和总结，包括将一些概念（整除、同余、群、环、域、多项式等代数学基础）重点记录下来，这样容易快速记忆一些重点，建立信息安全需要掌握的数学基础。然而，这里没有相应的证明，需要详细的证明可以翻书查阅。若有错误的地方，欢迎指正，本人将不断完善。(本人耗时一整天码字不易，不喜勿喷，希望对你有所帮助，仅供参考)

参考书籍《信息安全数学基础教程》(第2版)，许春香 周俊辉等人编著。

附：也可直接下载PDF学习，可能里面对应的标注和内容更直观、清晰和完整。

一、整除与同余

定义1.1：假设$a、b$ 是任意两个整数，其中 $b$ 非零，若存在一个整数$q$，使得
$$a=qb$$
则称为$b$能整除$a$，或称$a$能被$b$整除，记为$b|a$，且$b$是$a$的因子，$a$是$b$的倍数。

• 设$c>0$是两个不全为零的整数$a、b$的公因子，若$a、b$的任何公因子都整除c，则称为$a、b$的最大公因子。记为$c=(a,b)$，或者$c=gcd(a,b)$。假设$a、b$是两个非零的整数，则存在两个整数$u、v$使得 $(a,b)=ua+vb$。
• 设$m>0$是两个整数$a、b$的公倍数，若$m$整除$a、b$的任何公倍数，则$m$称为$a、b$的最小公倍数，记为$m=[a,b]$，或者$m=lcm(a,b)$。有$[a,b]=\frac{|ab|}{(a,b)}$，若$(a,b)=1$，则$[a,b]=|ab|$。

元素$a、b$互素的充要条件是，存在$u、v$使$ua+vb=1$，则由$(a,b)|(ua+vb)$，得$(a,b)|1$，所以$(a,b)=1$。

• 对于正整数$n$和整数$a$，$a^{-1}modn$存在的充分必要条件为$(a,n)=1$

如：$a^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}n)\Rightarrow$存在整数 $b$ 使得$ab(\mathrm{m}\mathrm{o}\mathrm{d}n)=1$。

• 例1：$7^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}13)=？$解：因为$7\ast 2(\mathrm{m}\mathrm{o}\mathrm{d}13)=1$，所以$7^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}13)=2$。

定义1.2：设$x\in R$，$\le x$的最大整数称为$x$的整数部分，记为$\lfloor x\rfloor$。其中$\lfloor x\rfloor \le x\le \lfloor x\rfloor +1$。

定义1.3：给定称为模的正整数$m$，若$m$除整数$a、b$得相同的余数，即存在整数$q_1$和$q_2$使得
$$a=q_{1}m+r，b=q_{2}m+r$$
则称$a$和$b$关于模$m$同余，记为
$$a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$$
$a$和$b$关于模$m$同余的充分必要条件为：$m|(a-b)$，即$a=b+mt$，$t$是整数。

• 第一章小结：（1) 重点记住”整除“和”被整除“的关系，通常为小的数整除大的数，大的数被小的数整除；(2) 注意$gcd=(a,b)$表示最大公因子(greatest common divisor, gcd），$lcm=[a,b]$表示最小公倍数(least common multiple, lcm)；（3）需要注意定义1.2中是$\lfloor x\rfloor$不是$[x]$。

二、群

2.1 群

定义2.1：设$S$是一个非空集合，如果在$S$上定义了一个代数运算，称为乘法 ·，记为$a\cdot b$。对于乘法，根据习惯可省略乘号写成$ab$ ，且满足下列条件，则称$(S,\cdot )$ 为一个半群。

• $S$关于乘法 · 是封闭的，即对于$S$中任意元素$a、b$，有$a\cdot b$ 属于$S$。
• $S$对于乘法 ·，结合律成立，即对于$S$中任意元素$a、b、c$ ，有$a\cdot (b\cdot c)=(a\cdot b)\cdot c$。

则用”乘法“定义的群称为乘法半群；用”加法“定义的群称为加法半群。

• 半群必须满足封闭性和结合律；
• 另外群还要满足左单元元$e\cdot (e\cdot a=a)$和左逆元$b\cdot (b\cdot a=e)$；
• 若群中的运算满足交换律，则这个群称为交换群或阿贝尔(Abel)群；
• 若群$G$中元素的个数是无限多个，称为$G$是无限群，若有限个，称为有限群，$G$中元素的个数称为群的阶，记为$|G|$。

2.2 子群

定义2.2：一个群$G$的一个子集$H$如果对于$G$的乘法构成一个群，则称为$G$的子群。

• (1) 对于任意群$G$都至少有两个子群：一个是群$G$本身，另一个是包含单位元的子集$e$，它们称为平凡子群，其他称为真子群。
  • $G$的单位元和子集H的单位元是同一的；
  • 若$a\in H$，且$a^{-1}$是$a$ 在$G$ 中的逆元，则$a^{-1}\in H$。
• (2) 非空子集H构成一个子群的充分必要条件是：
  • 对于任意的$a，b\in H$，有$ab\in H$；（封闭性）
  • 对于任意的$a\in H$，有$a^{-1}\in H$。（逆元）
• (3)一个集合$A$到另一个集合$B$的映射$f$是对于任意$a\in A$，都有唯一确定的
  $$b=f(a)\in B$$
  与之对应。$b$称为$a$在$f$下的像，而$a$称为$b$在$f$下的原像，如下图。

对于任意$a，b\in A$ ，如果$a\ne b$ ，有$f(a)\ne f(b)$，则称为$f$为单射。对于任意$b\in B$ ，总有$a\in A$，使$f(a)=b$，则称$f$为满射。既是满射又是单射的映射称为一一映射。单射的含义是$A$中的不同的元素在B中有不同的像。满射是$B$中的每个元素都成为$A$中元素的一个像。

• 第二章小结：(1) 要理解半群和群G的区别，半群要满足结合律和封闭性，群则是不仅要满足结合律和封闭性，而且需要满足存在左(右)单位元和左(右)逆元；(2) 理解封闭性、逆元的含义，以及”像“和”原像“等概念。

三、循环群与群的结构

3.1 循环群

定义3.1：如果一个群$G$里的元素都是某一个元素$g$的幂，则$G$称为循环群，$g$称为$G$的一个生成元。由$g$生成的循环群记为$(g)$或$⟨g⟩$。

• 无限循环群可表示为：{ $...,g^{-2},g^{-1},g^0,g^1,g^2,...$}，其中 $g^0=e$。
• 有限n阶循环群可表示为：{ $g^0,g^1,g^2,...,g^n$}, 其中$g^0=e$。

循环群的几个性质：

• （1）循环群是交换群；
• （2）在$n$阶循环群中，有$g^n=e$；
• （3）由于$n$阶循环群中$g^n=e$，则可以得到：设$i、j$是任意整数，如果$i=j(\mathrm{m}\mathrm{o}\mathrm{d}n)$，则
  $$g^i=g^j$$
  $g^i$的逆元为$g^{-i}=g^{n-i}$。

3.2 剩余类群

特殊的循环群——剩余类群。

由同余概念，将全体整数$Z$进行分类，设$m$是正整数，把模$m$同余的整数归为一类，即可表示为
$$a=qm+r，0⩽r<m，q=0,\pm 1,\pm 2,...$$
的整数是一个模$m$为一类，称为剩余类，剩余类中的每个数都称为该类的剩余或代表，$r$称为该类的最小非负剩余。

• 例如模8的剩余类为
  $\overline{0}=${ $0,\pm 8,\pm 2\times 8,\pm 3\times 8,...$ }
  $\overline{1}=${ $1,1\pm 8,1\pm 2\times 8,1\pm 3\times 8,...$ }
  $\overline{2}=${ $2,2\pm 8,2\pm 2\times 8,2\pm 3\times 8,...$ }
  …
  $\overline{7}=${ $7,7\pm 8,7\pm 2\times 8,7\pm 3\times 8,...$ }

定理3.1：模$m$的全体剩余类集合对于剩余类加法构成$m$阶循环群。注意对于加法，元素的“幂”就是元素的连加。

• 第三章小结：（1）需要记住循环群的几个性质；（2）剩余类往往在其上方加一横杠，即 $\overline{0}、\overline{1}、\overline{2}$这种方式。

四、环

定义4.1：设$R$是一非空集合，在$R$上定义了加法和乘法两种代数运算，分别记为“$+$”和“ $\cdot$ ”，如果R具有如下性质：

• (1) $R$ 对于加法$+$是一个交换群；
• (2) $R$ 对于乘法 $\cdot$ 是封闭的；
• (3) 乘法满足结合律，即对于任意$a、b、c\in R$，有$a\cdot (b\cdot c)=(a\cdot b)\cdot c$；
• (4) 分配律成立，即对于任意$a、b、c\in R$，有$a\cdot (b+c）=a\cdot b+a\cdot c$，(b+c)·a=b·a+c·a。

则称$(R,+,\cdot )$为一个环。环对于加法构成交换群，对于乘法满足封闭性和结合律，又对加法和乘法满足分配律。如果环$R$关于乘法还满足交换律，即对于任意，总有，则称$R$为交换环。

全体整数集合$Z$构成的环是交换环。

由于环里存在两种运算，因此把加法群的单位元称为零元，记为$0$，元素的加法逆元称为负元，记为$-a$。而继续把乘法单位元和乘法逆元分别称为单位元和逆元，用$1$和$a^{-1}$表示。

定义4.2：如果在一个环$R$里$a\ne 0$，$b\ne 0$，但
$$ab=0$$

则称$a$是这个环的一个左零因子，$b$是这个环的一个右零因子。显然交换环里每个左零因子同时是右零因子。若左右零因子同时存在，则称为零因子。

4.1 整环、除环与域

定义4.3：如果一个环$R$满足下列条件：

• (1) $R$是交换环；
• (2) 存在单位元，且$1\ne 0$；
• (3) 没有零因子。

则$R$称为整环。整数环、全体有理数、全体实数和全体复数都是整环。
条件(2)中$1\ne 0$意味着环中不止一个元素，或存在非零元。

定义4.4：若一个环$R$存在非零元，而且全体非零元构成一个乘法群，则$R$称为除环。全体**有理数$Q$、全体实数$R$和全体复数$C$**对于普通的加法和乘法都是除环。

定义4.5：一个交换除环称为一个域 。如果一个环$F$存在非零元，而且全体非零元构成一个乘法交换群，则$F$称为一个域。全体有理数$Q$、全体实数$R$和全体复数$C$对于普通的加法和乘法都是域。

当$p$ 是素数时，模$p$剩余类集合对于剩余类加法和乘法构成一个域，记为$GF(p)$。

从群的角度出发，则一个集合$F$是一个域应该满足以下3个条件：

• (1) 构成加法交换群；
• (2) 非零元构成乘法交换群；
• (3) 满足分配律。

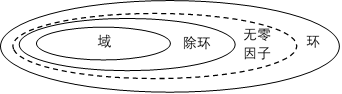
从域、除环、无零因子环和环的定义，可以知道域一定是除环，除环一定是无零因子环。

4.2 环的同态与理想

定义4.6：$(R,+,\cdot )$和 $(R^{{}^{\prime }},\oplus ,\otimes )$是两个环，如果存在$R$到$R^{{}^{\prime }}$的一个映射 $f$，加法和乘法都在$f$ 下得到保持，即对任意
$$f(ab)=f(a)f(b)$$
$$f(a+b)=f(a)+f(b)$$

则称$f$是$R$到$R^{{}^{\prime }}$同态映射，或简称同态。如果$f$ 是单射，则称为$f$是单同态。如果$f$ 是满射，则称为$f$是满同态。如果$f$ 是一一映射，则称$f$ 是同构(映射)，此时称$(R,+,\cdot )$和 $(R^{{}^{\prime }},\oplus ,\otimes )$是同构，并用$R\cong R^{{}^{\prime }}$表示。

• 第四章小结：(1) 整环与除环的区别：除环少了交换性，增加了乘法群。相同处：都有单位元，都是无零因子环；不同处：前者可以是零环，而后者不行；(2) 整环的优点（可换性）与除环的优点（可逆性）凑合在一起，就成了——域；(3) 集合F是一个域需要满足三个条件：构成加法交换群、非零元构成乘法交换群和满足分配律；(4）域一定是除环，除环包含了域。

五、多项式环与有限域

5.1 多项式环

定义5.1：设$F$是一个域，设$a\ne 0$。则称
$$f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_0（a_i\in F,n是非负整数)$$

• (1) $f(x)$是$F$上的一元$n$次多项式，其中$x$是一个未定元。
• (2) 称$a_n{x}^n$为$f(x)$的首项，$n$是多项式$f(x)$的次数，记为$deg(f(x))=n$。
• (3) 如果$a_n=1$，则称$f(x)$为首一多项式。
• (4) 如果$f(x)=a_n\ne 0$，则约定$deg(f(x))=0$，为零次多项式。
• (5) $F$上的全体一元多项式的集合用$F(x)$表示。
• (6) 当$a_i$全为$0$时，即$f(x)=0$，称为零多项式。

域$GF(2)$上的两个多项式$(GF(2)$的两个元素表示为$0$和$1$)

定理5.1：$F[x]$是具有单位元的整环。

定义5.2：对于$f(x)、g(x)\in F[x]$，$f(x)\ne 0$。如果存在$q(x)\in F[X]$，使得$g(x)=q(x)f(x)$，则称$f(x)$整除$g(x)$，记为$f(x)|g(x)$，$f(x)$称为$g(x)$的因式。如果$(f(x){)}^k|g(x)$，但$(f(x){)}^{k+1}|g(x)$不能整除g(x)，则称$f(x)$是$g(x)$的$k$重因式。

定理5.2：欧几里得算法。对于多项式$f(x)、g(x)$，其中$deg(f(x))⩽deg(g(x))$。反复进行欧几里得算法，得到下列方程式：
$g(x)=q_1(x)f(x)+r_1(x),deg(r_1(x))<deg(f(x))$
$f(x)=q_2(x)r_1(x)+r_2(x),deg(r_2(x))<deg(r_1(x))$
$r_1(x)=q_3(x)r_2(x)+r_3(x),deg(r_3(x))<deg(r_2(x))$
…
$r_{m-2}(x)=q_m(x)r_{m-1}(x)+r_m(x),deg(r_m(x))<deg(r_{m-1}(x))$
$r_{m-1}(x)=q_{m+1}(x)r_m(x)+r_3(x)$于是有$r_m(x)=(f(x),g(x))$
定义5.3：设$p(x)\in F[x]$为一多项式，且$deg(p(x))\ge 1$，如果$p(x)$在 $F[x]$内的因式仅有零次多项式及$cp(x)(c\ne 0\in F)$ ，则称$p(x)$是$F[x]$内的一个不可约多项式，否则称为可约多项式。

$GF(2)[x]$（二元域上，判断一次因式，只需把$0$和$1$代入，判断是否为$0$，为$0$则为可约，不为$0$不可约）四次以内的不可约多项式。

• (1) 0次，多项式为1；
• (2) 1次，多项式为$x,x+1$；
• (3) 2次，多项式为$x^2+x+1$；
• (4) 3次，多项式为$x^3+x^2+1,x^3+x+1$；
• (5) 4次，多项式为$x^4+x+1,x^4+x^3+1,x^4+x^3+x^2+x+1$；

在$GF(2)[x]$上有$(f(x)+g(x){)}^2=(f(x){)}^2+(g(x){)}^2$

5.2 多项式剩余类环

定义5.4：设$f(x)\in F[x]$是首一多项式。对于$a(x)、b(x)\in F[x]$，如果$f(x)$除$a(x)、b(x)$ 得相同的余式，即
$$a(x)=q_1(x)f(x)+r(x)$$
$$b(x)=q_2(x)f(x)+r(x)$$

则称$a(x)$和$b(x)$关于$f(x)$模同余，记为
$$a(x)\equiv b(x)(\mathrm{m}\mathrm{o}\mathrm{d}f(x))$$
定理5.3：设$f(x)\in F[x]$是一个首一多项式，且$deg(f(x))>0$，则$F[x](\mathrm{m}\mathrm{o}\mathrm{d}f(x))$构成具有单位元的交换环，称为多项式剩余类环。

定理5.4：如果$f(x)$是$F$上的首一不可约多项式，则$F[x](\mathrm{m}\mathrm{o}\mathrm{d}f)(x)$构成有限域。

5.3 有限域

定义5.5：有限个元素构成的域称为有限域或$Galois$(伽罗瓦)域。域中元素的个数称为有限域的阶。

• 例：当$p$是素数时，模$p$剩余类集合
  $$\{\overline{0},\overline{1},\overline{2},...,\overline{p-1}\}$$
  构成$p$阶有限域$GF(p)$。

定义5.6：$q$阶有限域中阶为$q-1$的元素称为本原域元素，简称本原元。

定理5.5：有限域中一定含有本原元。在一个无零因子环$R$里所有非零元的加法阶都相同。当加法阶有限时，它是一个素数。

定义5.7：域中非零元的加法阶称为环的特征，当加法阶为无限大时，称特征为$0$。如果一个域F不再含有真子集作为$F$的子域，则称$F$为素域。

定理5.6：阶为素数的有限域必为素域。

• (1) 素数$p$阶域的特征为$p$。
• (2) 任何素数$p$阶域与$GF(2)$同构。

定理5.7：有限域的阶必为其特征之幂。一般有限域记为$GF(p^m)$，其中$p$是域的特征，$m$是正整数。由于特征总是素数，则有限域的阶总为素数的幂。

• 第五章小结：（1）要注意零次多项式是只有常数项的多项式，零多项式是等于0；（2) 欧几里得和不可约多项式非常重要，需要多加深理解；（3）有限域则是必须掌握的知识点。

六、同余式

6.1 剩余系

回顾剩余类：设$m$是正整数，模$m$同余的全体整数是一个模$m$剩余类，即可表示为
$$a=qm+r，0⩽r<m，q=0,\pm 1,\pm 2,...$$

的整数是一个模$m$为一类，称为剩余类，剩余类中的每个数都称为该类的剩余或代表，$r$称为该类的最小非负剩余。

定义6.1：从模$m$剩余类中各取一个代表，则称这些代表的集合为模$m$的一个完全剩余系。

定义6.2：如果一个模$m$的剩余类里面的数与m互素，则称它为与模$m$互素的剩余类。从与模$m$互素的每个剩余类中各取一个数构成的集合称为模$m$的一个简化剩余系。

定理6.1：模$m$剩余类环中与$m$互素的剩余类构成乘法群。

欧拉函数$\phi (m)$表示小于或等于$m$的正整数中与$m$互质的数的数量。例如$\phi (8)=4$ ，因为$1、3、5、7$均和$8$互质(互素)。当$m$为质数时$\phi (m)=m-1$ ，以及 $\phi (p^k)=p^k(1-\frac{1}{p})$。

(欧拉定理)：设$m$是正整数，如果$(r,m)=1$ ，则
$$r^{\phi (m)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)$$

(费马定理)：如果$p$是素数，则
$$r^p\equiv r(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

6.2 中国剩余定理

通常中国剩余定理是求解同余式组的解，例
$$x\equiv b_1(\mathrm{m}\mathrm{o}\mathrm{d}m{)}_1$$
$$x\equiv b_2(\mathrm{m}\mathrm{o}\mathrm{d}m{)}_2$$
$$⋮$$
$$x\equiv b_k(\mathrm{m}\mathrm{o}\mathrm{d}m{)}_k$$

(中国剩余定理)：设$m_1,m_2,\dots ,m_k$两两互素，则上面的同余式组有唯一解。
$$x\equiv M_1^{-1}{M}_1{b}_1+M_2^{-1}{M}_2{b}_2+⋮+M_k^{-1}{M}_k{b}_k(\mathrm{m}\mathrm{o}\mathrm{d}m)$$
其中$m=m_1{m}_2\dots m_k$, $M_1={\frac{m}{m}}_i$，$M_1^{-1}{M}_1\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}{m}_i)$，$i=1,2,...,k$。

• 例：求解以下同余式组的解
  $$x\equiv 2(\mathrm{m}\mathrm{o}\mathrm{d}3)$$
  $$x\equiv 3(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  $$x\equiv 2(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  解答过程如下：
  $$m_1=3,m_2=5,m_3=7,m=3\times 5\times 7=105$$
  $$M_1=5\times 7=35,M_1^{-1}=2(\mathrm{m}\mathrm{o}\mathrm{d}3)$$
  $$M_2=3\times 7=21,M_2^{-1}=1(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  $$M_3=3\times 5=15,M_3^{-1}=1(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$x\equiv M_1^{-1}{M}_1{b}_1+M_2^{-1}{M}_2{b}_2+M_3^{-1}{M}_3{b}_3\equiv 2\times 35\times 2+1\times 21\times 3+1\times 15\times 2\equiv 23(\mathrm{m}\mathrm{o}\mathrm{d}15)$$
• 第六章小结：相同剩余的一个剩余类中有一个元素与$m$互素，则其中所有元素都与$m$互素。

七、平方剩余

定义7.1：设$p$是奇素数，即大于2的素数，如果二次同余式

有解，则$a$称为模$p$的平方剩余，否则$a$称为模$p$的平方非剩余。有些也将平方剩余和平方非剩余分别称为二次剩余和二次非剩余。

• 例：求出$p=5、7$时的平方剩余和平方非剩余。
  解：$p=5$时，由于
  $$1^2\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  $$2^2\equiv 4(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  $$3^2\equiv 4(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  $$4^2\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}5)$$
  所以$1、4$是模$5$的平方剩余，而$2、3$是模$5$的平方非剩余
  $p=7$时，由于
  $$1^2\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$2^2\equiv 4(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$3^2\equiv 2(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$4^2\equiv 2(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$5^2\equiv 4(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  $$6^2\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}7)$$
  所以$1、2、4$是模$7$的平方剩余，而$3、5、6$是模$7$的平方非剩余。

定理7.1：设$p$是奇素数。在模$p$的简化剩余系中，有 $\frac{p-1}{2}$个平方剩余， $\frac{p-1}{2}$个平方非剩余。

(欧拉判别式)：设$p$是奇素数，$(a,p)=1$ 。$a$是模$p$平方剩余的充分必要条件是
$$a^{\frac{p-1}{2}}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$$
$a$是模$p$平方非剩余的充分必要条件是
$$a^{\frac{p-1}{2}}\equiv -1(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

7.1 勒让德符号

由于在模乘法的计算过程中需要反复的模乘运算，上节平方剩余与平方非剩余的欧拉判别法当$p$比较大时并不方便，例如判别286在模563下是否是平方剩余，计算量非常大。而勒让德符号判别是否是平方剩余是非常有效。

定义7.2：设$p$是奇素数 ，$a$是整数。勒让德(Legendre)符号($\frac{a}{p}$)定义如下：
$$(\frac{a}{p})=\{\begin{array}{ll}1,& \text{a是模p的平方剩余}\\ -1,& \text{a是模p的非平方剩余}\\ 0,& \text{a能够被p整除，即p∣a}\end{array}$$
定理7.2：设$p$是奇素数，$a$是整数，则
$$(\frac{a}{p})=a^{\frac{p-1}{2}}(\mathrm{m}\mathrm{o}\mathrm{d}p)$$
勒让德符号具有下列性质：

• (1) $(\frac{1}{p})=1,(\frac{-1}{p})=(-1{)}^{\frac{p-1}{2}}$
• (2) 如果$a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}p)$，则$(\frac{a}{p})=(\frac{b}{p})$
• (3) $(\frac{a+p}{p})=(\frac{a}{p})$
• (4) 如果$(a,p)=1$，则$(\frac{a^2}{p})=1$
• (5) $(\frac{a_1{a}_2...a_n}{p})=(\frac{a_1}{p})(\frac{a_2}{p})...(\frac{a_n}{p})$

定理7.3：（二次互反律）如果$p、q$都是奇素数，$(p,q)=1$ ，则$(\frac{q}{p})=(-1{)}^{\frac{p-1}{2}\frac{q-1}{2}}(\frac{p}{q})$

• 第七章小结：使用勒让德符号的计算过程中，一定要注意$p$是奇素数。

八、总结

基本感念比较多，而且特别多的定义和定理，需要先记住慢慢理解，并结合书本上的证明加深理解。