Dijkstra 路径规划算法在二维仿真环境中的应用 -- Python代码实现
在上一节中,介绍了 Dijkstra 算法的原理以及在图中的应用,这一节将一步步实现 Dijkstra 路径规划算法在二维环境中的路径规划,来进一步加深对 Dijkstra 算法的理解。
所需要用到的 python 库为 matplotlib 和 math。
二维环境的搭建
我们将搭建下图所示的二维环境,其中黑色原点围成的为墙壁障碍物,绿色点为起点(30, 30),红色点为目标点(70,70)。后面需要将所示环境地图转换为栅格地图,所以在此设置栅格地图中栅格的大小为:1.0, 设置移动机器人的半径为: 2.0。
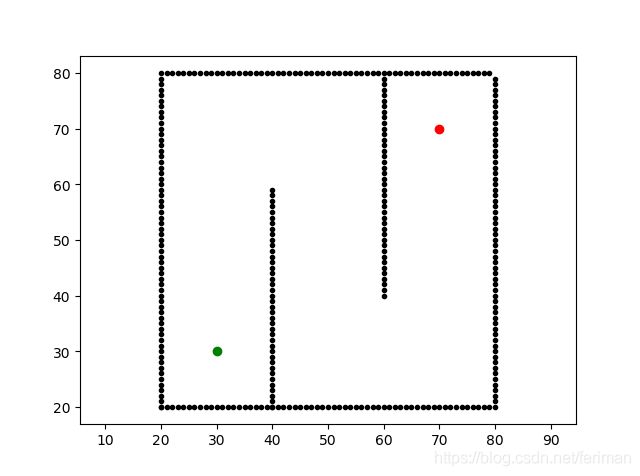
实现上述环境的代码如下:
# 设置起点,终点
sx, sy = 30, 30
gx, gy = 70, 70
gird_size = 1.0 # 栅格的大小
robot_radius = 2.0 # 机器人的半径
# 设置环境地图
ox, oy = [], []
# 设置四条边
for i in range(20, 80): # 下边
ox.append(i)
oy.append(20.0)
for i in range(20, 80): # 右边
ox.append(80.0)
oy.append(i)
for i in range(20, 80): # 上边
ox.append(i)
oy.append(80.0)
for i in range(20, 80): # 左边
ox.append(20)
oy.append(i)
# 设置内部的障碍物
for i in range(20, 60):
ox.append(40)
oy.append(i)
for i in range(40, 80):
ox.append(60)
oy.append(i)
if show:
plt.plot(ox, oy, '.k')
plt.plot(sx, sy, 'og')
plt.plot(gx, gy, 'or')
plt.axis('equal')
plt.show()
根据二维环境地图构建栅格地图
根据二维环境地图构建栅格地图的思路是:
- 由二维环境地图的数据,可以得到地图的四条边界值,左边界:
min_x,右边界:max_x,上边界:max_y,下边界:min_y。 - 根据四条边界值以及我们设置的栅格的大小,可以的栅格地图中栅格的行数和列数,即每一行栅格的数量:
y_grid_num,每一列栅格的数量:x_grid_num。 - 有了栅格的行数以及列数,可以将栅格地图初始化为一个二维数组,初始化每个栅格的占据状态都为
False,即没有被占据。 - 扫描二维环境,将障碍物占据的栅格设置为
True,表示该栅格被障碍物占据,机器人无法到达。栅格化后,机器人一步一个栅格,即一个栅格就表示机器人可能到达的一个位置,通过计算障碍物到栅格的距离(即障碍物到机器人的距离)与机器人的半径作比较,从而判断该栅格机器人能否到达。到达不了的栅格,将设置为True。
def calc_obstacle_grid_map(self, ox, oy):
""" 构建环境栅格地图 """
# 1. 获取环境的 上、 下、 左、 右 四个边界值
self.min_x = round(min(ox))
self.max_x = round(max(ox))
self.min_y = round(min(oy))
self.max_y = round(max(oy))
# 2. 根据四个边界值和栅格的大小计算 x, y 方向上 栅格的数量
self.x_grid_num = round((self.max_x - self.min_x) / self.grid_size)
self.y_grid_num = round((self.max_y - self.min_y) / self.grid_size)
# 3. 初始化环境栅格地图
self.obstacle_map = [[False for _ in range(self.x_grid_num)] for _ in range(self.y_grid_num)]
# 4. 将障碍物占据栅格
"""
遍历每一个 栅格(前两个 for 循环)以及 遍历每一个障碍物(后两个循环), 并计算障碍物到栅格的距离
比较该距离和机器人半径的大小,判断该栅格是否应该被障碍物占据
"""
for ix in range(self.x_grid_num):
for iy in range(self.y_grid_num):
x = self.calc_position(ix, self.min_x)
y = self.calc_position(iy, self.min_y)
for iox, ioy in zip(ox, oy):
d = math.sqrt((iox - x)**2 + (ioy - y)**2)
if d <= self.robot_radius:
self.obstacle_map[ix][iy] = True
break
其中 ,calc_position() 函数计算的栅格在二维环境中的坐标,其代码如下:
def calc_position(self, index, min_p):
""" 将栅格转化成在二维环境中的坐标 """
pos = min_p + index * self.grid_size
return pos
机器人运动模式
有了栅格地图,接着设置机器人的运动模式,即机器人如何在栅格地图中运动以及运动的消耗是多少。在此设置机器人可以朝着 8 个方向运动,即 上、下、左、右、右上、右下、左上、左下。代码实现如下:
def get_motion_model():
# dx, dy, cost
model = [
[0, 1, 1], # 上
[0, -1, 1], # 下
[-1, 0, 1], # 左
[1, 0, 1], # 右
[1, 1, math.sqrt(2)], # 右上
[1, -1, math.sqrt(2)], # 右下
[-1, -1, math.sqrt(2)], # 左下
[-1, 1, math.sqrt(2)] # 左上
]
return model
至此,环境的搭建以及机器人的属性都已设置完毕。为了方便后序进行路径规划,将每一个栅格表示为一个结点,代码实现如下:
class Node:
def __init__(self, x, y, cost, parent_index):
self.x = x # 栅格的 x 轴索引
self.y = y # 栅格的 y 轴索引
self.cost = cost # g(n)
self.parent_index = parent_index # 当前节点的父节点
接下来就可以进行 Dijkstra 路径规划了。
Dijkstra 路径规划
在此回顾上节中所说的代码框架。
实现代码如下:
def planning(self, sx, sy, gx, gy):
""" 进行路径规划 """
# 1. 将机器人的坐标进行结点化
sx_index = self.calc_xy_index(sx, self.min_x)
sy_index = self.calc_xy_index(sy, self.min_y)
gx_index = self.calc_xy_index(gx, self.min_x)
gy_index = self.calc_xy_index(gy, self.min_y)
start_node = self.Node(sx_index, sy_index, 0.0, -1)
goal_node = self.Node(gx_index, gy_index, 0.0, -1)
# 2. 初始化 open_set, close_set,并将起点放进 open_set 中
open_set, close_set = dict(), dict()
open_set[self.calc_index(start_node)] = start_node
# 3.开始循环
while True:
# (1). 取 open_set 中 cost 最小的结点
c_id = min(open_set, key=lambda o: open_set[o].cost)
current = open_set[c_id]
if show: # 展现路径规划的过程
plt.plot(self.calc_position(current.x, self.min_x),
self.calc_position(current.y, self.min_y), "xc")
if len(close_set.keys()) % 10 == 0:
plt.pause(0.001)
# (2). 判断该节点是否为终点
if current.x == goal_node.x and current.y == goal_node.y:
print('Find Goal!')
goal_node.parent_index = current.parent_index
goal_node.cost = current.cost
break
# (3). 将该节点从 open_set 中取出,并加入到 close_set 中
del open_set[c_id]
close_set[c_id] = current
# (4). 根据机器人的运动模式,在栅格地图中探索当前位置出发到达的下一可能位置
for move_x, move_y, move_cost in self.robot_motion:
node = self.Node(current.x + move_x,
current.y + move_y,
current.cost + move_cost, c_id)
n_id = self.calc_index(node)
if n_id in close_set:
continue
if not self.verify_node(node):
continue
if n_id not in open_set:
open_set[n_id] = node # 发现新的结点
else:
if open_set[n_id].cost >= node.cost:
# 当前节点的路径到目前来说是最优的,进行更新
open_set[n_id] = node
rx, ry = self.calc_final_path(goal_node, close_set)
return rx, ry
-
路径规划是在结点的基础上进行的,而机器人的起点给的是在二维环境中的坐标,所以首先需要将机器人在二维环境中的坐标转化为栅格地图中坐标,然后再转化成结点表示。其中,二维环境的坐标转化为栅格地图中的坐标的函数为:
calc_xy_index(),其代码实现如下:def calc_xy_index(self, pos, min_p): """ 将机器人在二维环境地图中的坐标转化成栅格地图中的坐标 """ index = round((pos - min_p) / self.grid_size) return index -
初始化
open_set,closed_set,并将起点放入到open_set中。第一步中已经得到了栅格结点化后的起点,为了方便在open_set以及closed_set中索引查找,在此再次对栅格结点进行标号索引,标号方式为从左下角向右一行一行进行编号索引。实现函数为:calc_index(),具体实现代码如下:def calc_index(self, node): """ 将栅格结点化后的地图进行编号索引,从左下角向右一行一行进行编号索引,如下面示例共 9 个节点,编号方式为: [7, 8, 9] [4, 5, 6] [1, 2, 3] """ index = node.y * self.x_grid_num + node.x return index -
开始循环查找路径。
-
取出
open_set中 cost 最小的结点。 -
判断该结点是否为终点。如果是,则说明找到目标点,退出循环。
-
将第一步从
open_set中取出的结点加入到closed_set中。 -
根据机器人的运动模式,在栅格地图中探索当前位置出发到达的下一可能位置,并更新
open_set。其中,在探索可能到达的下一位置时,需要判断下一位置是否有效,即是否在所给的环境当中以及是否处在障碍物上。这个验证函数为:verify_node(),实现代码如下:def verify_node(self, node): """ 验证机器人的当前位置是否合理 """ px = self.calc_position(node.x, self.min_x) py = self.calc_position(node.y, self.min_y) # 检查当前位置是否在环境内 if px < self.min_x or px > self.max_x: return False if py < self.min_x or py > self.max_y: return False # 检查当前位置是否处于障碍物中 if self.obstacle_map[node.x][node.y]: return False return True
-
-
找到目标点后,进行路径回溯。从目标点开始向前回溯,直到回溯到起点。回溯函数为:
calc_final_path(),实现代码如下:def calc_final_path(self, goal_node, close_set): """ 从终点开始进行回溯,生成从起点到终点的最优路径 """ rx = [self.calc_position(goal_node.x, self.min_x)] ry = [self.calc_position(goal_node.y, self.min_y)] parent_index = goal_node.parent_index while parent_index != -1: n = close_set[parent_index] rx.append(self.calc_position(n.x, self.min_x)) ry.append(self.calc_position(n.y, self.min_y)) parent_index = n.parent_index return rx, ry
各个地图之间坐标的转化关系为:
地图表示示例如下:
完整代码如下:
import matplotlib.pyplot as plt
import math
class Dijkstra:
def __init__(self, ox, oy, grid_size, robot_radius):
# 初始化地图的情况
self.min_x = None
self.max_x = None
self.min_y = None
self.max_y = None
self.x_grid_num = None
self.y_grid_num = None
self.obstacle_map = None
self.grid_size = grid_size
self.robot_radius = robot_radius
self.calc_obstacle_grid_map(ox, oy) # 构建环境栅格地图
self.robot_motion = self.get_motion_model()
def calc_obstacle_grid_map(self, ox, oy):
""" 构建环境栅格地图 """
# 1. 获取环境的 上、 下、 左、 右 四个边界值
self.min_x = round(min(ox))
self.max_x = round(max(ox))
self.min_y = round(min(oy))
self.max_y = round(max(oy))
# 2. 根据四个边界值和栅格的大小计算 x, y 方向上 栅格的数量
self.x_grid_num = round((self.max_x - self.min_x) / self.grid_size)
self.y_grid_num = round((self.max_y - self.min_y) / self.grid_size)
# 3. 初始化环境栅格地图
self.obstacle_map = [[False for _ in range(self.x_grid_num)] for _ in range(self.y_grid_num)]
# 4. 将障碍物占据栅格
"""
遍历每一个 栅格(前两个 for 循环)以及 遍历每一个障碍物(后两个循环), 并计算障碍物到栅格的距离
比较该距离和机器人半径的大小,判断该栅格是否应该被障碍物占据
"""
for ix in range(self.x_grid_num):
for iy in range(self.y_grid_num):
x = self.calc_position(ix, self.min_x)
y = self.calc_position(iy, self.min_y)
for iox, ioy in zip(ox, oy):
d = math.sqrt((iox - x)**2 + (ioy - y)**2)
if d <= self.robot_radius:
self.obstacle_map[ix][iy] = True
break
def planning(self, sx, sy, gx, gy):
""" 进行路径规划 """
#
# 1. 将机器人的坐标进行结点化
sx_index = self.calc_xy_index(sx, self.min_x)
sy_index = self.calc_xy_index(sy, self.min_y)
gx_index = self.calc_xy_index(gx, self.min_x)
gy_index = self.calc_xy_index(gy, self.min_y)
start_node = self.Node(sx_index, sy_index, 0.0, -1)
goal_node = self.Node(gx_index, gy_index, 0.0, -1)
# 2. 初始化 open_set, close_set,并将起点放进 open_set 中
open_set, close_set = dict(), dict()
open_set[self.calc_index(start_node)] = start_node
# 3.开始循环
while True:
# (1). 取 open_set 中 cost 最小的结点
c_id = min(open_set, key=lambda o: open_set[o].cost)
current = open_set[c_id]
if show: # pragma: no cover
plt.plot(self.calc_position(current.x, self.min_x),
self.calc_position(current.y, self.min_y), "xc")
# for stopping simulation with the esc key.
# plt.gcf().canvas.mpl_connect(
# 'key_release_event',
# lambda event: [exit(0) if event.key == 'escape' else None])
if len(close_set.keys()) % 10 == 0:
plt.pause(0.001)
# (2). 判断该节点是否为终点
if current.x == goal_node.x and current.y == goal_node.y:
print('Find Goal!')
goal_node.parent_index = current.parent_index
goal_node.cost = current.cost
break
# (3). 将该节点从 open_set 中取出,并加入到 close_set 中
del open_set[c_id]
close_set[c_id] = current
# (4). 根据机器人的运动模式,在栅格地图中探索当前位置出发到达的下一可能位置
for move_x, move_y, move_cost in self.robot_motion:
node = self.Node(current.x + move_x,
current.y + move_y,
current.cost + move_cost, c_id)
n_id = self.calc_index(node)
if n_id in close_set:
continue
if not self.verify_node(node):
continue
if n_id not in open_set:
open_set[n_id] = node # 发现新的结点
else:
if open_set[n_id].cost >= node.cost:
# 当前节点的路径到目前来说是最优的,进行更新
open_set[n_id] = node
rx, ry = self.calc_final_path(goal_node, close_set)
return rx, ry
def calc_final_path(self, goal_node, close_set):
""" 从终点开始进行回溯,生成从起点到终点的最优路径 """
rx = [self.calc_position(goal_node.x, self.min_x)]
ry = [self.calc_position(goal_node.y, self.min_y)]
parent_index = goal_node.parent_index
while parent_index != -1:
n = close_set[parent_index]
rx.append(self.calc_position(n.x, self.min_x))
ry.append(self.calc_position(n.y, self.min_y))
parent_index = n.parent_index
return rx, ry
class Node:
def __init__(self, x, y, cost, parent_index):
self.x = x # 栅格的 x 轴索引
self.y = y # 栅格的 y 轴索引
self.cost = cost # g(n)
self.parent_index = parent_index # 当前节点的父节点
#
# def __str__(self):
# return str(self.x) + "," + str(self.y) + "," + str(self.cost) + "," + str(self.parent_index)
def calc_index(self, node):
"""
将栅格化后的地图进行编号索引,从左下角向右一行一行进行编号索引,如下面示例
[7, 8, 9]
[4, 5, 6]
[1, 2, 3]
"""
index = node.y * self.x_grid_num + node.x
return index
def calc_xy_index(self, pos, min_p):
""" 将机器人在二维环境地图中的坐标转化成栅格地图中的坐标 """
index = round((pos - min_p) / self.grid_size)
return index
def calc_position(self, index, min_p):
""" 将栅格地图的坐标转化成在真实环境中的坐标 """
pos = min_p + index * self.grid_size
return pos
def verify_node(self, node):
""" 验证机器人的当前位置是否合理 """
px = self.calc_position(node.x, self.min_x)
py = self.calc_position(node.y, self.min_y)
# 检查当前位置是否在环境内
if px < self.min_x or px > self.max_x:
return False
if py < self.min_x or py > self.max_y:
return False
# 检查当前位置是否处于障碍物中
if self.obstacle_map[node.x][node.y]:
return False
return True
@staticmethod
def get_motion_model():
# dx, dy, cost
model = [
[0, 1, 1], # 上
[0, -1, 1], # 下
[-1, 0, 1], # 左
[1, 0, 1], # 右
[1, 1, math.sqrt(2)], # 右上
[1, -1, math.sqrt(2)], # 右下
[-1, -1, math.sqrt(2)], # 左下
[-1, 1, math.sqrt(2)] # 左上
]
return model
def main():
# 设置起点,终点
sx, sy = 30, 30
gx, gy = 70, 70
gird_size = 1.0 # 栅格的大小
robot_radius = 2.0 # 机器人的半径
# 设置环境地图
ox, oy = [], []
# 设置四条边
for i in range(20, 80): # 下边
ox.append(i)
oy.append(20.0)
for i in range(20, 80): # 右边
ox.append(80.0)
oy.append(i)
for i in range(20, 80): # 上边
ox.append(i)
oy.append(80.0)
for i in range(20, 80): # 左边
ox.append(20)
oy.append(i)
# 设置内部的障碍物
for i in range(20, 60):
ox.append(40)
oy.append(i)
for i in range(40, 80):
ox.append(60)
oy.append(i)
if show:
plt.plot(ox, oy, '.k')
plt.plot(sx, sy, 'og')
plt.plot(gx, gy, 'or')
# plt.grid('True')
plt.axis('equal')
# plt.show()
dijkstra = Dijkstra(ox, oy, gird_size, robot_radius)
rx, ry = dijkstra.planning(sx, sy, gx, gy)
if show:
plt.plot(rx, ry, '-r')
plt.pause(0.01)
plt.show()
if __name__ == '__main__':
show = True
main()
如果本文对您有帮助,记得在下方点赞呦!欢迎在评论区留言讨论!
