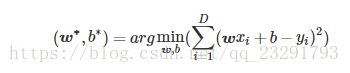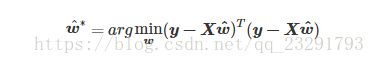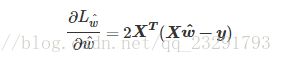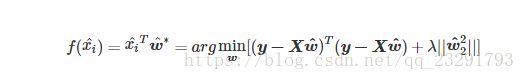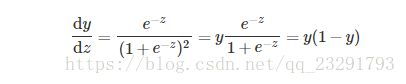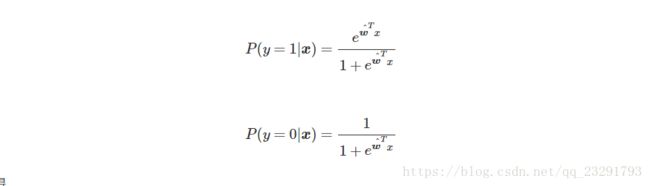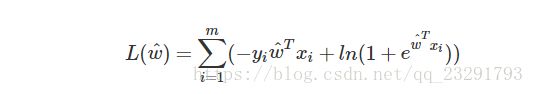《机器学习》 线性模型

        线性模型的形式很简洁，而且易于建模。线性模型蕴含着机器学习中一些重要的基本思想.许多功能更为强大的非线性模型可在线性模型的基础上通过引入层次结构或高维映射而得。线性模型还有多种推广形式,常见的有广义线性模型：逻辑回归、岭回归等。

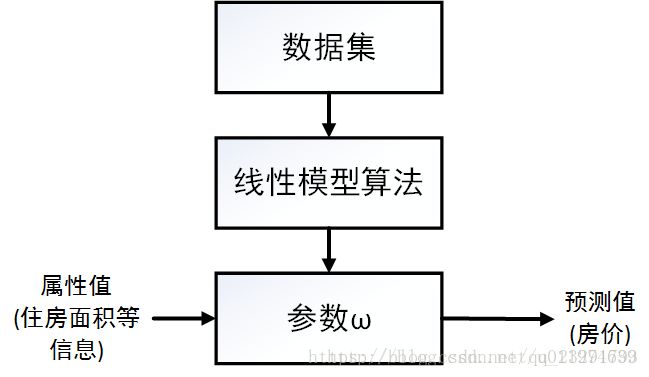
1.线性回归模型

（1）问题的求解目标

        线性回归(linear regression)是一种回归分析技术，例如在给定数据集 D 。 线性回归试图学习到一个线性模型以尽可能准确地预测实值输出标记 。通过在数据集上建立线性模型， 建立代价函数 (loss function),最终以优化代价函数为目标确定模型参数

w和b,从而得到模型用以后续的预测。整个线性回归算法流程如下:

                                       

       那么问题的核心就转换为求目标参数w和b,根据已知的数据集D ：

                          

        来计算参数w和b，对于给定的样本数据xi，其预测值为，这时候我们需要一个可以衡量预测值与数据集真实值之间差距的函数，我们称之为代价函数，可想而知如果代价函数在整个数据集上的值越小，就代表的预测值与真实值越接近，而这就是我们想要的，所以我们的优化目标就是让代价函数的值最小。

        这里代价函数我们选用均方误差(square loss)，则在整个数据集D上，模型的代价函数为：

                                    

        我们的要确定的参数为，使得: 

                                                    

        这样的基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method,LSM)。

（2）如何去求解w与b

        优化目标由上面可以确定，接下来就是如何对参数w和b进行求解。求解w 和b使L（f）最小化的的过程，称为线性回归模型的最小二乘“参数估计”(parameter estimation)。由凸优化知识可知，L(w,b)是关于w 和b的凸函数(证明略过)，在数学上我们可知，在凸函数上当函数在导数为0处取极值，同时极值就是函数的最值。故当L(w,b)关于w 和b的导数均为零时，得到ww和b的最优解。

        我们考虑更为一般的情况，在数据集D上，样本由d个属性描述，此时线性回归又称为“多元线性回归”。为了便于讨论，我们把w和b统一记为w=(w;b)。与之对应的，数据集D表示为一个m⋅(d+1)大小的矩阵X,表示为：

                                                 

        可以得到新的优化目标表达式为: 

                                                                          

        新的代价函数为：

                                                                               

        我们进行相应求导：

                                                                                

         令上式为零，可以得到最优闭式解，此时需要分类讨论：

                      
① 如果XTX为满秩矩阵或正定矩阵时，可得：

                                                  

                        此时，线性回归模型为：

                                                                    

                           ②如果XTX不是满秩矩阵时(样本数量小于属性数量)，X的行数大于列数，必然不满秩，存在多个解析解，它们都能使得损失函数最小化，选择哪一个解析解作为输出，由学习算法的归纳偏好决定，这时候常常引入正则化(regularization)项.常见的正则化项如L1正则化或L2正则化，我们以L2正则化为例:

                            

                       则线性回归模型为: 

                                                      

（3）线性回归总结

                                                                           

2.广义线性模型

        当我们希望线性模型的预测值逼近真实标记值yy时，就得到了线性回归模型.为了便于观察，我们简写线性回归模型为y=wTx+b ，此时我们可以让线性回归模型去逼近y的其他目标，例如lny。照着这个想法，我们可以更一般地，考虑单调可导函数h(⋅),令h(y)=wTx+bh(·)，这样wTx+bw可以逼近一个h(⋅)，如果我们选好的h(⋅)就可以使用线性模型去逼近不同的函数了，我们称这样的模型为广义线性模型(generalized linear model). 上述表达式可以记为:

                                                                

        有一个典型的例子，当h(⋅)=ln(⋅)h(·)=ln(·) 时广义线性模型就是对数线性回归，即：

                                                                            

       可以看到，虽然是叫广义线性模型，其实大部分时候变换函数都是非线性变换，即实质上已经是非线性的。

3.对数几率回归

（1）如何用线性回归进行分类

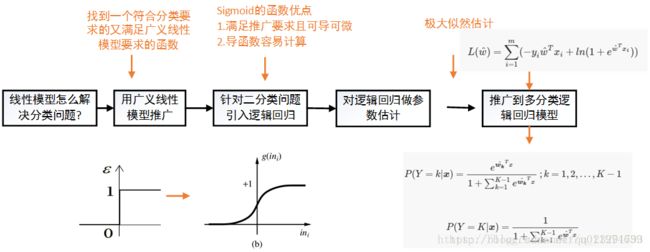
        在一开始我们说到，回归分析本质上是一个函数估计问题，就是找出因变量和自变量之间的因果关系。如果因变量是连续值那就叫回归，如果因变量是离散值那就叫分类。前面说的都是使用线性模型进行回归学习，下面我们就说说怎么用线性模型做分类。其实用线性模型做分类的办法已经在上一节介绍，就是广义线性模型,考虑到在广义线性模型中，如果我们找到一个单调可微函数h(⋅)h(·)可以将分类任务和线性回归联系到一起，那就可以用线性模型完成分类任务了。

（2）什么样的函数能讲线性回归转换成分类函数

    这里，我们先简化分类任务，考虑二分类问题，即预测值为y=0或y=1,考虑到z=wTx+b的取值z为(−∞,+∞),如果我们有这样一个理想函数(信号分析里面的阶跃函数):

                       

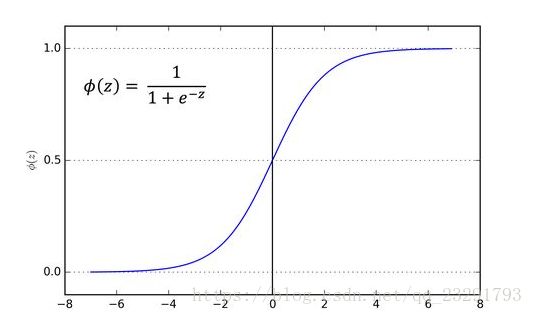
        当z<0取值为0时即取负例，z>0时取值为1时即取正例，可以看到，这样的函数能够很好的解决分类问题。这样的函数能作为广义线性模型里面的h(⋅)吗？答案是不能。这是因为这样的函数有一个问题：函数不连续故不可导。那我们能不能找到一个类似这样的函数，并且连续可导?答案当然是有的，例如对数概率函数(logistic function)，下图为对数概率函数的示意图:

                                            

    由图可以看出对数概率函数将自变量zz转化为一个接近0或者1的y值，且输出值在z=0处变化剧烈，重要的是对数概率函数满足连续可微的条件，故我们可将对数概率函数和广义线性模型结合到一起:

                                                                    

        为什么我们非要选用这样的一个函数，难道就是因为它连续可微和阶跃函数很像就足够了吗? 那么下面这些函数也有类似的性质： 

        为啥不选它们，这个其实是考虑到对数概率函数的导函数，我们看一下它的导函数形式: 

                                                                 

        对数概率函数的导函数可以直接通过原函数很方便的计算出来，我们做参数估计时是需要作求导操作的，函数有这样的特性是非常方便的。也就是它在众多函数中脱颖而出的原因之一。

（3）怎么计算参数

        在进行分类的时候，对应类别的概率：

        上面我们说了可以通过极大似然法来估计w^，在给定数据集{(xi,yi)}，逻辑回归模型的对数似然函数为: 

        而因为有 ：

        带入可求得：

                                        

        上式关于w^的高阶可导连续凸函数，可用梯度下降法或者拟牛顿法求解。

（4）总结

4.线性判别分析（LDA）

    线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的线性学习方法，思想是:

• 训练时:设法将训练样本投影到一条直线上，使得同类样本的投影点尽可能地接近、异类的样本投影点尽可能的远
• 预测时:将待预测样本投影到学到的直线上，根据它的投影点的位置判断类别

    两类样本的线性判别分析示意图如下: 

        这里你可能会想，为什么非要投影搞来搞去的这么麻烦， 为啥不是在两类样本中找到一条直线分开两类样本就好 ，，这样的方法就是 支持向量机 (support vector machine,SVM)的思想。后面会再介绍SVM.

(转载地址：https://blog.csdn.net/u011974639/article/details/77102663点击打开链接)