循序渐进，深入理解KMP算法

KMP算法是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。其中第一位就是《计算机程序设计艺术》的作者！

KMP算法要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。说白了，就是关键字搜索。模式串就是关键字（接下来称它为P），如果它在一个主串（接下来称为T）中出现，就返回它的具体位置，否则返回-1（常用手段）。

常规的暴力匹配算法时间复杂度：O(m*n)，而KMP算法目的是尽快解决字符串匹配问题，时间复杂度为O(m+n)。

1、暴力匹配算法（脑补一下就好，不用看的）

首先，对于这个问题有一个很单纯的想法：从左到右一个个匹配，如果这个过程中有某个字符不匹配，就跳回去，将模式串向右移动一位。这有什么难的？

我们可以这样初始化：

之后我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动，如果不一致，如下图：

A和E不相等，那就把i指针移回第1位（假设下标从0开始），j移动到模式串的第0位，然后又重新开始这个步骤：

代码：

public class Demo{
	public static int bf(String ts,String ps) {
		char[] t = ts.toCharArray();
		char[] p = ps.toCharArray();
		int i = 0; // 主串的位置
		int j = 0; // 模式串的位置
		while (i < t.length && j < p.length) {
		    if (t[i] == p[j]) { // 当两个字符相同，就比较下一个
		    		i++;
		    		j++;
		    }else {
		    		i = i - j + 1; // 一旦不匹配，i后退
		    		j = 0; // j归0
		    }
	    }
		if (j == p.length) {
			return i - j;
	     }else {
	        return -1;
	     } 
	    }
}

2、KMP算法（重点）

算法的改进之处在于：每当一趟匹配过程中出现字符比较不相等时，指向主串的指针 i 不倒退，而是利用已经得到的“部分匹配”的结果，将模式串向右滑动尽可能远的一段距离后，继续比较。

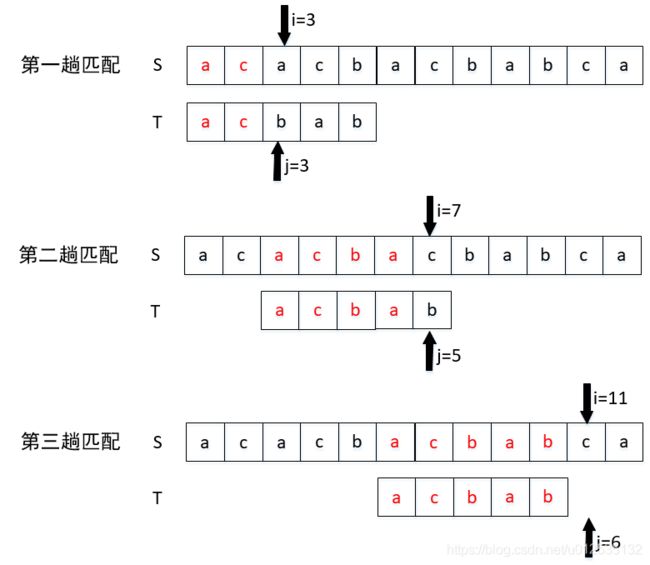
例如：主串S："acacbacbabca"，模式串P："acbab"

只进行了三趟比较，就匹配上了，是不是很厉害。我们可以注意到整个过程 i 是不往回走的，所以时间复杂度为O(n+m)。

使用这个算法，需要解决两个问题：

1. 比较不成功时，模式串T向右滑动多少距离
2. 滑动之后，模式串T的工作指针 j 的值

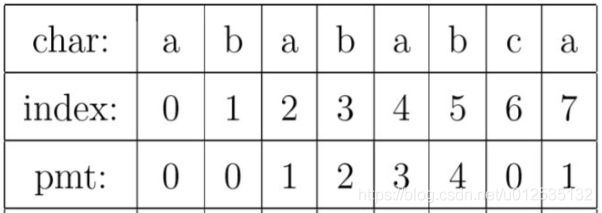
为了解决这两个问题，我们需要引入一个数组PMT：

我先解释一下字符串的前缀和后缀。如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。同样可以定义后缀A=SB， 其中S是任意的非空字符串，那就称B为A的后缀，例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。要注意的是，字符串本身并不是自己的后缀。

有了这个定义，就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长 度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。再比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。

例如index=4时，考察字符串”ababa”的最大相等k前缀和k后缀，最大值为3：

前缀串	后缀串
a	a
ab	ba
aba	aba
abab	baba

但是一般在编程中不用PMT，而是用next数组计算。

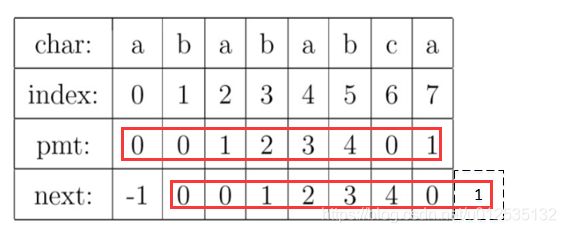
为了编程的方便， 我们不直接使用PMT数组，而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是，在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。

则next[j]表示： 前j-1位，字符串的前缀集合与后缀集合的交集中最长元素的长度。

 

我们来通过例子，观察next数组是如何解决，之前的两个问题的：

1. 比较不成功时，模式串T向右滑动多少距离
2. 滑动之后，模式串T的工作指针 j 的值

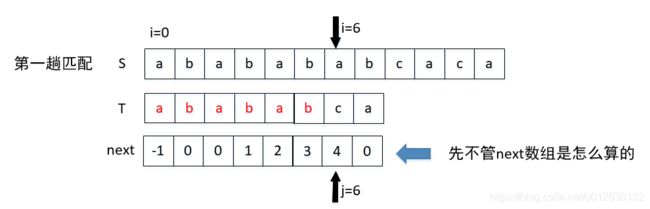
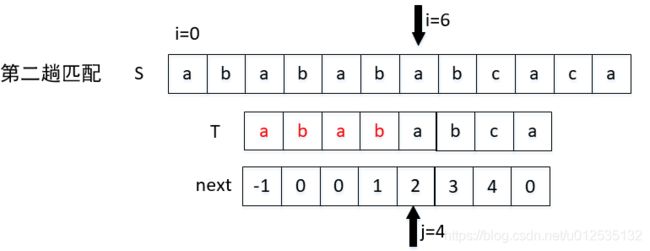
当发生不相等的情况时( S[i] != T[j] )：此时next[6]=4，这个时候让 S[6]要和T[4]比较（j = next[j]）：

 KMP代码：

	//返回第一个匹配上的起始位置
	public  static int KMP(String text, String pattern) {
		int i = 0,j = 0;
		while(i=pattern.length())return i-pattern.length();//return i-j;
		return -1;
	}

 

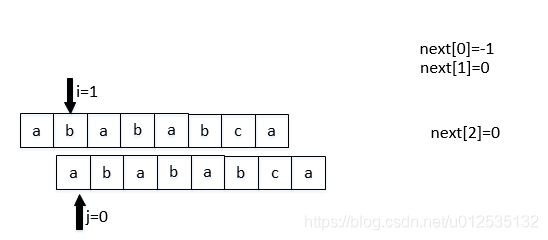
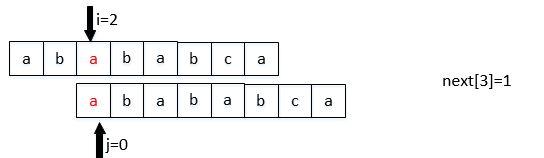
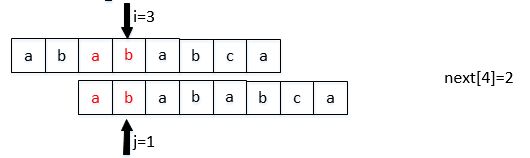
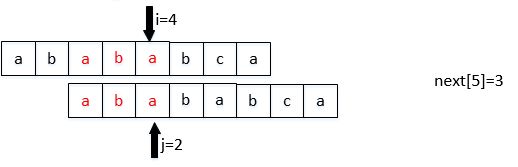
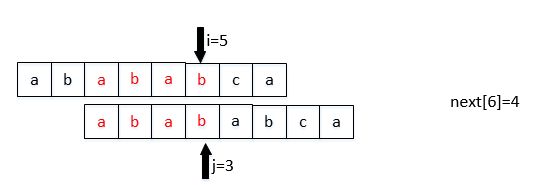
那么next数组如何计算呢？我们可以将它看成是两个相同串的匹配，初始位置差1位

next[j]表示： 前j-1位，字符串的前缀集合与后缀集合的交集中最长元素的长度。

next[2]算的是第0,1位，前缀集合与后缀集合的交集中最长元素的长度。

next数组计算代码，和KMP代码很像：

	public  static void getNext(String p, int []next)
	{
		next[0] = -1;
		int i = 0, j = -1;
		while (i < p.length())
		{
			if (j == -1 || p.charAt(i) == p.charAt(j))
			{
				++i;
				++j;
				next[i] = j;
			}	
			else
				j = next[j];
		}
	}

汇总两部分的代码：

public class KMP {
	public  static void getNext(String p, int []next)
	{
		next[0] = -1;
		int i = 0, j = -1;
		while (i < p.length())
		{
			if (j == -1 || p.charAt(i) == p.charAt(j))
			{
				++i;
				++j;
				next[i] = j;
			}	
			else
				j = next[j];
		}
	}
	//返回第一个匹配上的起始位置
	public  static int KMP(String text, String pattern , int next[]) {
		int i = 0,j = 0;
		while(i=pattern.length())return i-pattern.length();//return i-j;
		return -1;
	}
	
	
	public static void print(int []a) {
		for(int i = 0 ; i < a.length ; i++) {
			System.out.print(a[i]+" ");
		}
	}
	public static void main(String[] args) {
		String s = "abcabcabdabba";
		String t = "abcabd";
		int a[] = new int[s.length()+1];
		getNext(s ,  a);
		int index = KMP(s,t,a);//返回第一个匹配的位置
		System.out.print(index);
	}
}

如有看不懂的地方，肯定是我没表达清楚，请留言，我会进一步修正。

 

参考资料：

• https://www.zhihu.com/question/21923021
• https://blog.csdn.net/v_july_v/article/details/7041827