Deep learning：三十三(ICA模型)

 

　   基础知识：

　　在sparse coding（可参考Deep learning：二十六(Sparse coding简单理解)，Deep learning：二十九(Sparse coding练习)）模型中，学习到的基是超完备集的，也就是说基集中基的个数比数据的维数还要大，那么对一个数据而言，将其分解为基的线性组合时，这些基之间本身就是线性相关的。如果我们想要得到线性无关的基集，那么基集中元素的个数必须小于或等于样本的维数，本节所讲的ICA（Independent Component Analysis，独立成分分析）模型就可以完成这一要求，它学习到的基之间不仅保证线性无关，还保证了相互正交。本节主要参考的资料见：Independent Component Analysis

　　ICA模型中的目标函数非常简单，如下所示：

 　　

　　它只有一项，也就是数据x经过W线性变换后的系数的1范数（这里的1范数是对向量而言的，此时当x是向量时，Wx也就是个向量了，注意矩阵的1范数和向量的1范数定义和思想不完全相同，具体可以参考前面一篇文章介绍的范数问题Deep learning：二十七(Sparse coding中关于矩阵的范数求导)），这一项也相当于sparse coding中对特征的稀疏性惩罚项。于系数性不同的是，这里的基W是直接将输入数据映射为特征值，而在sparse coding中的W是将特征系数映射重构出原始数据。

　　当对基矩阵W加入正交化约束后，其表达式变为：

 　　

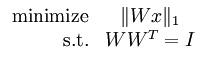
　　所以针对上面的目标函数和约束条件，如果要用梯度下降的方法去优化权值的话，则需要执行下面2个步骤：

 　　 

　　首先给定的学习率alpha是可以变化的（可以使用线性搜索算法来加速梯度下降过程，具体的每研究过，不了解），而Wx的1范数关于W的导数可以利用BP算法思想将其转换成一个神经网络模型求得，具体可以参考文章Deriving gradients using the backpropagation idea。此时的目标函数为：

　　

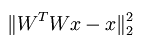
　　最后的导数结果为：

 　　

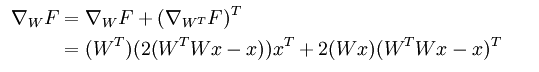
　　另外每次用梯度下降法迭代权值W后，需要对该W进行正交化约束，即上面的步骤2。而用具体的数学表达式来表示其更新方式描述为：

 　　

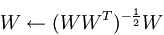
　　由于权值矩阵为正交矩阵，就意味着：

1. 矩阵W中基的个数比输入数据的维数要低。这个可以这么理解：因为权值矩阵W是正交的，当然也就是线性无关的了，而线性相关的基的个数不可能大于输入数据的维数。
2. 在使用ICA模型时，对输入数据进行ZCA白化时，需要将分母参数eplison设置为0，原因是上面W权值正交化更新公式已经代表了ZCA Whitening。这是网页教程中所讲的，真心没看懂。

　　另外，PCA Whitening和ZCA Whitening都是白化操作，即去掉数据维度之间的相关性，且保证特征间的协方差矩阵为单位矩阵。

 

 

　　参考资料：

     Deep learning：二十六(Sparse coding简单理解)

     Deep learning：二十九(Sparse coding练习)

     Independent Component Analysis

     Deep learning：二十七(Sparse coding中关于矩阵的范数求导)

     Deriving gradients using the backpropagation idea