蓝桥杯练习赛5--全解析
文章目录
- JAM计数法
-
- 解题思路
- 解题代码
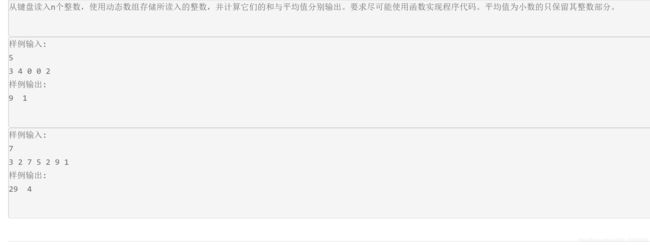
- 动态数组使用
- 输出米字型
-
- 解题思路
- 解题代码
- 排队打水问题
-
- 解题思路
- 解题代码
- 王、后传说
-
- 解题思路
- 解题代码
- 理财计划
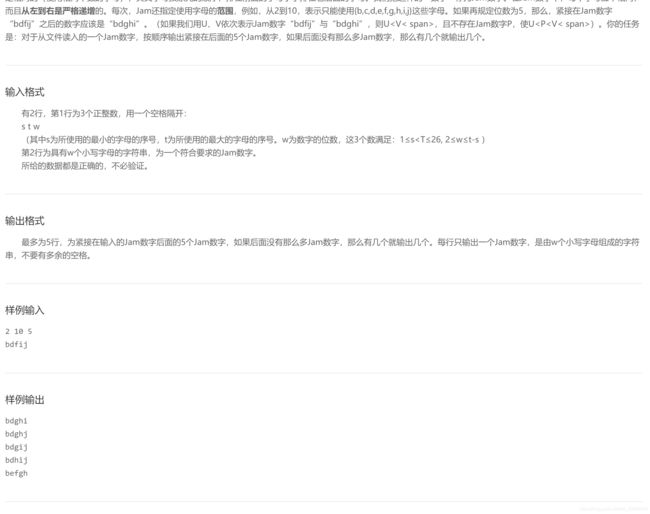
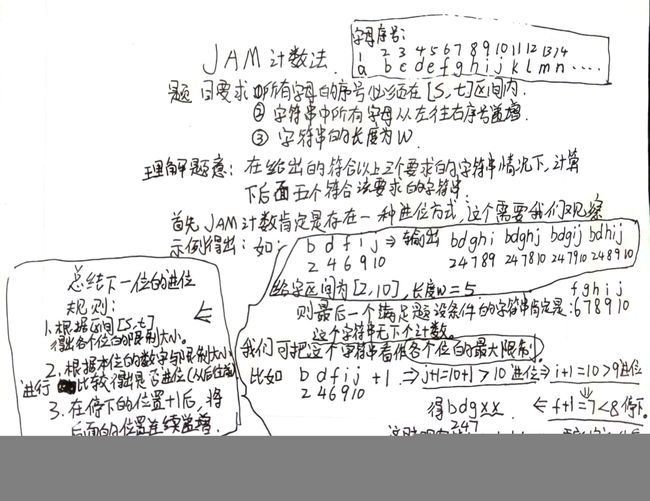
JAM计数法
解题思路
解题代码
#include动态数组使用
这题就不详解了。。
#include输出米字型
解题思路
建立用于遍历八个方向的方向数组,通过中间的数不断循环向外扩散。
解题代码
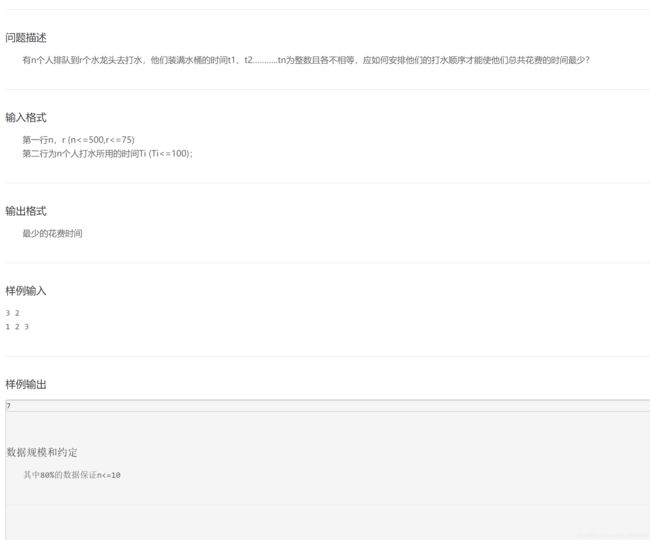
#include排队打水问题
解题思路
这题乍一看说输出最短时间,结果看测试示例就明白,是每个人的等待最短时间相加。。。
这个等待时间相加很明显,先排个序,然后以水龙头的个数进行数据分组,比如水龙头有3个,则第一组是前三个最快时间的人,第二组是后三个…一直往后,但是对于每一个人来说它的等待时间是连续的,所以需要连续继承的相加,说太多浪费时间,建议这个时候自己思考,然后再看代码,不然可能不会的永远不会,会的永远都会。。。
解题代码
#include王、后传说
解题思路
这就是标准的n皇后问题,需要用到回溯法
我的解题过程
- 创建棋盘,更新国王的位置,并且根据八个方向把边上的位置也标记。
- 以
行为基准,以回溯为方式向下放置皇后。 - 放置皇后之前需要判断是否可以放置皇后,可以通过check函数检查该位置的前面几行是否在
上、左上、右上三个方向出现过皇后'Q',一旦出现则该位置不能放置(由于是以行为方式放置,所以左右不可能出现’Q’),当然这题还需要检查是否为国王位。 - 只要到达了最后一行的下一行(
由于我是以0为初始,所以是row==n即可判断),则视为一次正确的棋盘皇后放置,答案更新一次。
可以看看之前的n皇后问题
n皇后问题
解题代码
#include理财计划
题目就是找出数学迭代关系,通过循环迭代多次即可得到最终的存款,而后减去本金,便得到利益。
#include