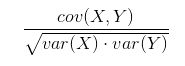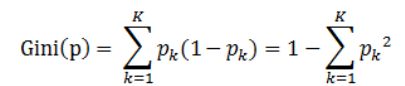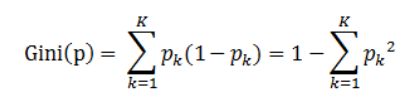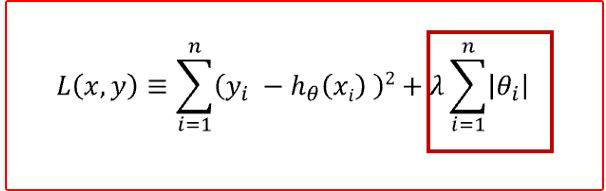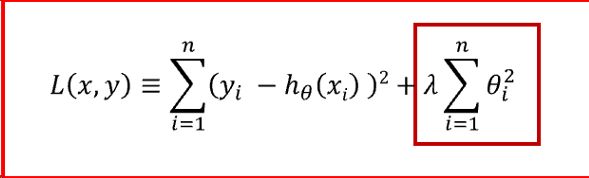多特征
多特征的情况可以分为两大类,一个是特征压缩或降维,一类是特征选择,当然业务模型来说广义上也可以都视为降维,减少了特征维度的数量,只是一种用的是模型来转换,一种是用特征选择来做。特征选择是基于原有的特征选择需要的,不改变原有特征,也即是维度空间没变化,而降维是基于PCA或SVD等,对特征空间进行了转变重构,形成了新的特征空间。
特征选择又分为三类,filter 过滤,wrapper包裹,embeding嵌入
压缩降维
PCA
PCA叫主成分分析,正如通俗叫压缩,浓缩的意思,就像我们说的浓缩洗衣液,浓缩果汁,这里都是精华啊,比如我们要榨个果汁,就可能要很多水果,但是我们如果分析了主要的元素,比如酸味,甜味的,还有主要营养,那么我们就可以浓缩出需要的味道,减少不必要的一些东西。
PCA就是这个道理,如果不降维,将导致数据分布在一个极小的区域内。也叫维度灾难。
那么PCA就是利用线性映射将数据投射到低维度的空间里,可以数据从原来的坐标系转换到新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,我们可以忽略余下的坐标轴,即对数据进行降维处理。
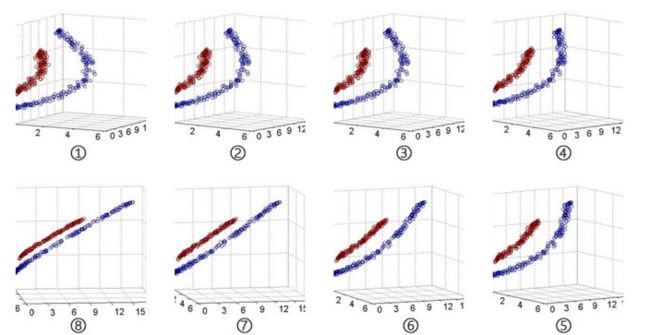
可以形象的看下图,从图①到图⑧的序列中可以看出,原始数据的分布呈现明显的曲线分布特征,而旋转后的数据样本则呈现直线分布特征
数学上就是利用线性代数的特征矩阵和特征根来求解,将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
PCA算法实现一般流程:
(1)对数据进行归一化处理;
(2)计算归一化后的数据集的协方差矩阵;
(3)计算协方差矩阵的特征值和特征向量;
(4)保留最重要的k个特征(通常k要小于n);
(5)找出k个特征值相应的特征向量
(6)将m * n的数据集乘以k个n维的特征向量的特征向量(n * k),得到最后降维的数据,由矩阵乘法知道数据行数没有变化,列数转为k。
PCA降维准则:
(1) 最近重构性:样本集中所有点,重构后的点距离原来的点的误差之和最小。
(2) 最大可分性:样本在低维空间的投影尽可能分开。
PCA算法优点:
(1)使得数据集更易使用;
(2)降低算法的计算开销;
(3)去除噪声;
(4)使得结果容易理解;
(5)完全无参数限制。
PCA算法缺点:
(1)如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高;
(2) 特征值分解有一些局限性,比如变换的矩阵必须是方阵;
(3) 在非高斯分布情况下,PCA方法得出的主元可能并不是最优的。
PCA的主要应用
(1)高维数据集的探索与可视化。
(2)数据压缩。
(3)数据预处理。
(4)图象、语音、通信的分析处理。
(5)降维(最主要),去除数据冗余与噪声。
from sklearn.decomposition import PCA
# 使用sklearn的PCA进行维度转换
x = [[3,2,5],[3,5,1]]
model_pca = PCA() # 建立PCA模型对象
model_pca.fit(x) # 将数据集输入模型
model_pca.transform(x) # 对数据集进行转换映射
components = model_pca.components_ # 获得转换后的所有主成分
components_var = model_pca.explained_variance_ # 获得各主成分的方差
components_var_ratio = model_pca.explained_variance_ratio_ # 获得各主成分的方差占比
print(components[:2]) # 打印输出前2个主成分
print(components_var[:2]) # 打印输出前2个主成分的方差
print(components_var_ratio) # 打印输出所有主成分的方差占比
[[ 2.66453526e-17 -6.00000000e-01 8.00000000e-01]
[-6.00000000e-01 -6.40000000e-01 -4.80000000e-01]]
[1.25000000e+01 2.46519033e-32]
[1.00000000e+00 1.97215226e-33]
svd
SVD叫奇异值分解,也是一种矩阵求解特征的方法,SVD算法不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。
我们对任意实数矩阵 的奇异分解过程,可以表示为:
其中 为对角矩阵,而它对角线上的元素就被称之为奇异值。矩阵 的列向量被称之为「左奇异向量」,矩阵 的列向量被称之为「右奇异向量」。当我们需要对矩阵的行数进行压缩时,我们使用到的组合就是:左奇异向量 + 奇异值。当我们是对矩阵的列数进行压缩降维时,我们使用到的就是:右奇异向量 + 奇异值。
同样,已知 ,求取 、、 的数学推导公式非常复杂,这里我们直接使用 NumPy 对其进行接求解。
我们使用 np.linalg.svd(a) 函数 对矩阵 A 进行奇异值分解,得到下面三个返回值:
- 第一个返回值:矩阵 的左奇异向量 。
- 第二个返回值:对角矩阵 的对角线上的值(对角矩阵除了对角线,其他位置的值都为 0 )。
- 第三个返回值,矩阵 的右奇异向量 的转置 。
import numpy as np
a = np.array([[1, 2, 3, 4], [5, 8, 6, 7], [1, 1, 1, 2]])
u, s, vh = np.linalg.svd(a) # vh 表示 v 的转置
print(u.shape, s.shape, vh.shape)
(3, 3) (3,) (4, 4)
def pca_svd(data):
# 进行svd 分解
u, s, v = np.linalg.svd(data)
# 这里选取前两个特征v[0:2]
# 然后计算低维空间数据
pc_svd = np.dot(data, v[:, 0:2])
return pc_svd
我们可以对比PCA和SVD,
PCA求解关键在于求解协方差矩阵的特征值分解
SVD关键在于的特征值分解。
通过数据维度变换进行降维是非常重要的降维方法,这种降维方法分为线性降维和非线性降维两种,
其中常用的代表算法包括独立成分分析(ICA)、主成分分析(PCA)、因子分析(Factor Analysis,FA)、
线性判别分析(LDA,也叫Fisher线性判别FLD)、局部线性嵌入(LLE)、核主成分分析(Kernel PCA)等。
PCA适用场合
1、非监督式类型的数据集。它是一种非监督式的降维方法,因此适用于不带有标签的数据集;而对于带有标签的数据集则可以采用LDA。
2、根据方差自主控制特征数量。最大的主成分的数量会<=特征的数量,这意味着,PCA也可以输出完全相同数量的特征,具体取决于选择特征中解释的方差比例。
3、更少的正则化处理。选择较多的主成分将导致较少的平滑,因为我们将能够保留更多的数据特征,从而减少正则化。
4、数据量较大的数据集。数据量大包括数据记录多和数据维度多两种情况,PCA对大型数据集的处理效率较高。
5、数据分布是位于相同平面上(非曲面),数据中存在线性结构。
接下来是特征选择的方法
经验法
这是一般适合变量较少或是开始探索的时候,我们一般可以先根据变量的方差进行初步筛选,当然这是初步探索的,简单说就是如果值都是一个,或大多数都是一样的,那这列的影响其实可以忽略。主要通过业务专家、数据专家的以往经验、实际数据情况、业务理解程度等综合考虑选择。业务经验依靠的是业务背景,从众多维度特征中选择对结果影响较大的特征。
filter过滤
这主要是基于数据,一般是看某个变量和目标变量之间的关联关系,主要通过统计学和信息学的方法来选择
卡方检验
这就是应用了统计学的思想,比如用卡方检测两个变量是否独立,例如性别和收入是否相关,做假设检验。做0假设是独立的,然后检测统计量的显著性,得到小于阈值则认为是可信就是独立。
但是这是统计里小样本的方式,做个表然后一般是0.05作为显著性水平,而对于机器学习是非常多的特征的,如果按照这个0假设,就是错误的选择是独立但是选择作为特征,如果有1000个变量就会有50个被错选可能,一般是不能只是用一个阈值,而是选择前k个,然后进入模型去看训练结果来评判。
这里就用了selectKBest库
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2 #卡方检验
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
model1 = SelectKBest(chi2, k=2)#选择k个最佳特征
model1.fit_transform(iris.data, iris.target)#iris.data是特征数据,iris.target是标签数据,该函数可以选择出k个特征
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[1.7, 0.4],
[1.4, 0.3],
[1.5, 0.2],
[1.4, 0.2],
[1.5, 0.1],
[1.5, 0.2],
[1.6, 0.2],
[1.4, 0.1],
[1.1, 0.1],
[1.2, 0.2],
[1.5, 0.4],
[1.3, 0.4],
[1.4, 0.3],
[1.7, 0.3],
[1.5, 0.3],
[1.7, 0.2],
[1.5, 0.4],
[1. , 0.2],
[1.7, 0.5],
[1.9, 0.2],
[1.6, 0.2],
[1.6, 0.4],
[1.5, 0.2],
[1.4, 0.2],
[1.6, 0.2],
[1.6, 0.2],
[1.5, 0.4],
[1.5, 0.1],
[1.4, 0.2],
[1.5, 0.2],
[1.2, 0.2],
[1.3, 0.2],
[1.4, 0.1],
[1.3, 0.2],
[1.5, 0.2],
[1.3, 0.3],
[1.3, 0.3],
[1.3, 0.2],
[1.6, 0.6],
[1.9, 0.4],
[1.4, 0.3],
[1.6, 0.2],
[1.4, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[4.7, 1.4],
[4.5, 1.5],
[4.9, 1.5],
[4. , 1.3],
[4.6, 1.5],
[4.5, 1.3],
[4.7, 1.6],
[3.3, 1. ],
[4.6, 1.3],
[3.9, 1.4],
[3.5, 1. ],
[4.2, 1.5],
[4. , 1. ],
[4.7, 1.4],
[3.6, 1.3],
[4.4, 1.4],
[4.5, 1.5],
[4.1, 1. ],
[4.5, 1.5],
[3.9, 1.1],
[4.8, 1.8],
[4. , 1.3],
[4.9, 1.5],
[4.7, 1.2],
[4.3, 1.3],
[4.4, 1.4],
[4.8, 1.4],
[5. , 1.7],
[4.5, 1.5],
[3.5, 1. ],
[3.8, 1.1],
[3.7, 1. ],
[3.9, 1.2],
[5.1, 1.6],
[4.5, 1.5],
[4.5, 1.6],
[4.7, 1.5],
[4.4, 1.3],
[4.1, 1.3],
[4. , 1.3],
[4.4, 1.2],
[4.6, 1.4],
[4. , 1.2],
[3.3, 1. ],
[4.2, 1.3],
[4.2, 1.2],
[4.2, 1.3],
[4.3, 1.3],
[3. , 1.1],
[4.1, 1.3],
[6. , 2.5],
[5.1, 1.9],
[5.9, 2.1],
[5.6, 1.8],
[5.8, 2.2],
[6.6, 2.1],
[4.5, 1.7],
[6.3, 1.8],
[5.8, 1.8],
[6.1, 2.5],
[5.1, 2. ],
[5.3, 1.9],
[5.5, 2.1],
[5. , 2. ],
[5.1, 2.4],
[5.3, 2.3],
[5.5, 1.8],
[6.7, 2.2],
[6.9, 2.3],
[5. , 1.5],
[5.7, 2.3],
[4.9, 2. ],
[6.7, 2. ],
[4.9, 1.8],
[5.7, 2.1],
[6. , 1.8],
[4.8, 1.8],
[4.9, 1.8],
[5.6, 2.1],
[5.8, 1.6],
[6.1, 1.9],
[6.4, 2. ],
[5.6, 2.2],
[5.1, 1.5],
[5.6, 1.4],
[6.1, 2.3],
[5.6, 2.4],
[5.5, 1.8],
[4.8, 1.8],
[5.4, 2.1],
[5.6, 2.4],
[5.1, 2.3],
[5.1, 1.9],
[5.9, 2.3],
[5.7, 2.5],
[5.2, 2.3],
[5. , 1.9],
[5.2, 2. ],
[5.4, 2.3],
[5.1, 1.8]])
# 查看p值和得分
model1.scores_ #得分
model1.pvalues_ #p
array([4.47651499e-03, 1.56395980e-01, 5.53397228e-26, 2.75824965e-15])
相关系数
统计学有很多相关系数,比较著名的是Pearson,spearman,kendall等
假设两个变量列,pearson相关系数的计算公式为:
cov(X,Y)表示两个变量的协方差,var(x)和var(y)表示的是方差,而从线性映射角度,上面是两个向量的乘,而下面是各自的长度,也就是相关系数就是当做一个夹角余弦
值在-1到1之间,负是负相关,这里注意是线性关系,也就是不线性相关并不代表不相关,因为可能是非线性相关。
pandas的corr函数可以计算,method中,有三种相关系数的计算方式,包括 —— 'pearson', 'kendall', 'spearman',常用的是线性相关pearson。
cc_pd = pd.DataFrame(cc_zscore.T, columns=['c1', 'c2'])
cc_corr = cc_pd.corr(method='spearman') #相关系数矩阵
计算积距pearson相关系数,连续性变量才可采用;
计算Spearman秩相关系数,适合于定序变量或不满足正态分布假设的等间隔数据;
计算Kendall秩相关系数,适合于定序变量或不满足正态分布假设的等间隔数据。
互信息
这里用到到了信息学的方法,信息熵来自信息系统,就是一个系统的不确定性程度,
具体说我们一个变量带来的不确定性就是取值的可能越多,那么信息量也越大,
最直观的一个特征,系统有它没它都差不多,也就是我们说的这列数据都很一致,那么对于你区分最终的目标其实就没有多少用,那这个有多少用就可以用信息熵来定量表达,有它时候和没它时候的信息量差别就是信息熵,系统越乱,信息熵就越高,如果一个是单选,一个是多选,前者的差别就可能比较小,所以,信息熵也可以说是系统有序化程度的一个衡量。
随机变量的不确定性也可以叫不纯度,
对于每一个可能的取值xi,其概率 P(X=xi) = pi , ( i = 1,2, ... , n)
因此随机变量X的熵:
信息增益
是指期望信息或者信息熵的有效减少量。
对于一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量。有它即信息熵,无它则是条件熵。
条件熵:计算当一个特征t不能变化时,系统的信息量是多少。
对于一个特征X,它可能的取值有n多种(x1,x2,……,xn),计算每个值的条件熵,再取平均值。
在决策树类模型里通常就是用信息增益的计算来划分选择特征
ID3算法使用的是信息增益
定义: 以某特征划分数据集前后的熵的差值
在熵的理解那部分提到了,熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
划分前样本集合D的熵是一定的 ,entroy(前),
使用某个特征A划分数据集D,计算划分后的数据子集的熵 entroy(后)
所以直观的说,
信息增益 = entroy(前) - entroy(后)
但是信息增益有偏向取值多的特征
所以有了C4.5算法
使用的是信息增益比
意为,信息增益比 = 惩罚参数 * 信息增益,
在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。所以信息增益比偏向取值较少的特征
所以就有了 基尼指数
这里是Cart算法使用,可以做分类和回归
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
说明:
pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
当为二分类是,Gini(P) = 2p(1-p)
基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率。
这样,我们在特征选择的时候可以从两个维度进行,一个是相关系数的判断,另一个就是信息增益的角度。相关系数侧重的是相关性,而信息增益和基尼指数可以挖掘深度的相关性,比如某个特征在一定其他特征划分之后才起到比较好的划分作用。
#sklearn计算互信息(信息增益),用metric的mutual_info_score
# 现计算样本label与样本特征之间一一的互信息
tf_idf_matrix_T = tf_idf_matrix.T
X_MI = {} # 用于存储tf_idf_matrix_T特征与label之间的互信息值
from sklearn import metrics as mr
import numpy as np
X_labels = np.array(X_labelnum)
for i in range(tf_idf_matrix_T.shape[0]):
X_MI[i] = mr.mutual_info_score(X_labels,tf_idf_matrix_T[i])
封装法(Wrapper)
主要思想就是类似启发式空间搜索,定义一个目标函数(AUC或是MSE),然后一个个特征加入,最终看是否加入这个变量。
递归消除特征法:递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,移除平方值最小的那个序号i对应的特征,再基于新的特征集进行下一轮训练。以此类推,直到剩下的特征数满足我们的要求为止。
优点: 直接面向算法优化, 不需要太多知识。缺点: 庞大的搜索空间, 需要定义启发式策略。
也可以是完全搜索,启发式搜索或是随机搜索
嵌入法(Embedded)
所谓正则化Regularization, 指的是在回归模型代价函数后面添加一个约束项, 在线性回归模型中,有两种不同的正则化项
- 所有参数绝对值之和,即L1范数,对应的回归方法叫做Lasso回归
-
所有参数的平方和,即L2范数,对应的回归方法叫做Ridge回归,岭回归
可以使用正则化的模型进行特征选择:L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,L2则鲁棒性稍差,但是要注意,L1没有选到的特征不代表不重要,原因是两个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验。
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X, y = iris.data, iris.target
X.shape
(150, 4)
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X, y)
model = SelectFromModel(lsvc, prefit=True)
X_new = model.transform(X)
X_new.shape
/usr/local/python37/lib/python3.7/site-packages/sklearn/svm/base.py:931: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
"the number of iterations.", ConvergenceWarning)
(150, 3)
树模型的特征选择(随机森林、决策树):训练能够对特征打分的预选模型:RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型。
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X, y = iris.data, iris.target
X.shape
(150, 4)
clf = ExtraTreesClassifier()
clf = clf.fit(X, y)
clf.feature_importances_
/usr/local/python37/lib/python3.7/site-packages/sklearn/ensemble/forest.py:246: FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22.
"10 in version 0.20 to 100 in 0.22.", FutureWarning)
array([0.12711344, 0.06636865, 0.32727393, 0.47924398])
model = SelectFromModel(clf, prefit=True)
X_new = model.transform(X)
X_new.shape
(150, 2)
另外还有很多嵌入的方式比如 GBDT,梯度提升树。
以及很多文本,图片的高维数据需要使用深度学习的特征抽取方式,一般图片或文字直接放入深度学习结构网络,不需要人为再去做特征工程。
特征构建
或叫做特征衍生,用现有的特征计算组合成新的特征;其实在图片和文本处理上更为需要,因为机器学习最后都是处理数值矩阵,而半结构化和非结构化的数据都需要经过转换才能被模型处理,另外这些在文本和图片有各自更多的方法,也有叫特征抽取或是预训练
这里主要举例结构化数据,例如天池二手车里,我们肯定关注二手车用了多久,但是里面只有买车时间和上架时间,所以要进行估算得出使用时间
import datetime as dt
# 使用时间:data['creatDate'] - data['regDate'],反应汽车使用时间,一般来说价格与使用时间成反比
# 不过要注意,数据里有时间出错的格式,所以我们需要 errors='coerce'
data['used_time'] = (pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') -
pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days