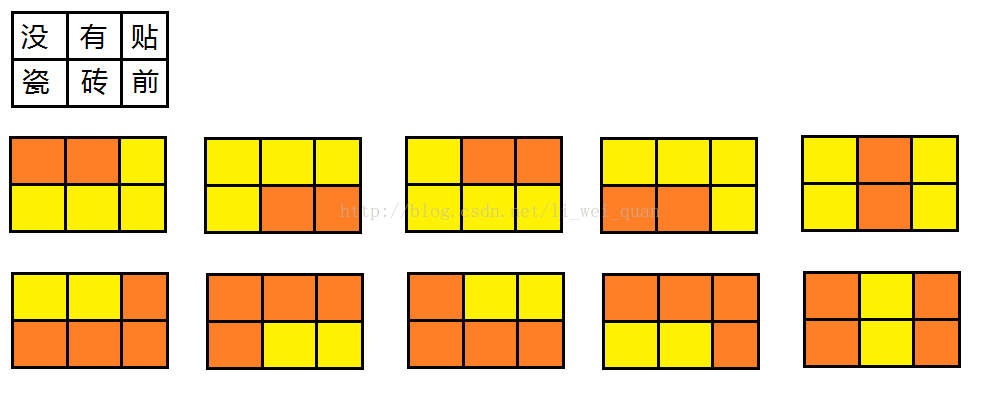2017年第八届“蓝桥杯”国赛B组C/C++ 个人题解
前言:
我参加了今年第八届的蓝桥杯国赛,只拿了个优秀奖,伤心。官方也没有公布试题和答案,在网上搜索了很久都没有找到蓝桥杯国赛的题目。突然有了一个不自量力的想法,趁还有一点记忆,把题目记录下来,并且附上自己的做法。
第一题:36进制
题意:
用类似16进制的表示办法,A表示10,B表示11,……,Y表示25,Z表示26,再加上0到9,就可以表示为36进制。那么请问MANY对应的十进制数是多少?
代码:
#include
int main()
{
char ch[5] = "MANY";
int ans = 0;
for(int i = 0; i < 4; i++)
ans = ans * 36 + (ch[i]-'A'+10);
printf("%d\n", ans);
return 0;
} 参考答案:1040254
第二题:瓷砖样式
题意:
有2种不同颜色规格为1*2的瓷砖,用其来铺设地板,不能重叠和越界。并且,地板中任意2*2的格子不能为同一种颜色。如图,当地板为2*3时,有10种铺设方案。问:当地板为3*10时,问有多少种铺设方案?
参考代码:
#include
#include
#include
using namespace std;
#define maxn 3
#define maxm 10
int a[maxn][maxm];
set ans;
bool check()
{
for(int i = 0; i < maxn-1; i++)
for(int j = 0; j < maxm-1; j++)
{
int p = a[i][j];
if(p == -1) return false; //地板必须全部铺满
if(p == a[i+1][j] && p == a[i][j+1] && p == a[i+1][j+1]) return false;
}
return true;
}
int arr2int(int arr[maxn][maxm])
{
int s = 0;
for(int i = 0; i < maxn; i++)
{
for(int j = 0; j < maxm; j++)
{
s = s * 2 + arr[i][j];
}
}
return s;
}
void dfs(int cur) //准备铺地板第cur格
{
if(cur == maxn * maxm)
{
if(check())
{
ans.insert(arr2int(a)); //把二位数组当作30位的二进制,转换成一个整数,用于去重
}
return;
}
int x = (cur-1) / maxm;
int y = cur - x * maxm -1;
//格子(x,y)已经铺有瓷砖
if(a[x][y] != -1)
dfs(cur+1);
//横着铺
if(y+1 < maxm && a[x][y] == -1 && a[x][y+1] == -1)
{
a[x][y] = a[x][y+1] = 0;
dfs(cur+1);
a[x][y] = a[x][y+1] = 1;
dfs(cur+1);
a[x][y] = a[x][y+1] = -1;
}
//竖着铺
if(x+1 < maxn && a[x][y] == -1 && a[x+1][y] == -1)
{
a[x][y] = a[x+1][y] = 0;
dfs(cur+1);
a[x][y] = a[x+1][y] = 1;
dfs(cur+1);
a[x][y] = a[x+1][y] = -1;
}
}
int main()
{
memset(a, -1, sizeof(a));
ans.clear();
dfs(1);
printf("%d\n", ans.size());
return 0;
} 参考答案:101466
注:此题感谢网友 @隽永啊 的提醒,之前的代码没有考虑到有样式会有重复,已经加入去重了,没有去重之前是105760个样式。
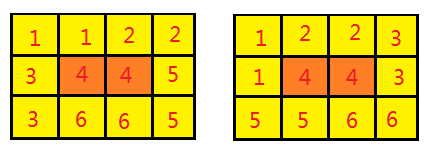
那什么时候会出现重复呢,看下面两个图就知道了,其他重复的样式类似。
相同数字表示同一个瓷砖,数字顺序表示dfs的时候铺瓷砖的顺序,虽然铺的方法不一样,但是最后得到的样式却一样。我是把二维数组转化成一个maxn*maxm位的二进制数,要是样式不一样的话,该二进制数对应的十进制数也肯定不一样,最后利用set容器去重即可。再顺带提一下,因为需要二进制转十进制,所以二维数组中的值用0和1来表示,转化的时候会方便一点。我看见有些人的题解是,用0表示没铺,1和2分别表示两种不同的瓷砖,这样在进制转换时麻烦很多。
第三题:希尔伯特曲线
题意:
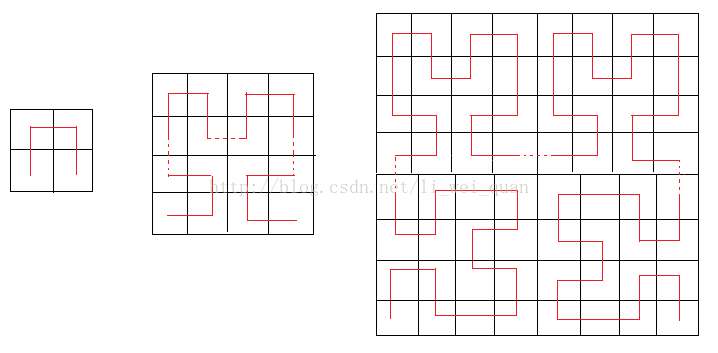
有一个正方形,可以在上面作出一条希尔伯特曲线。左下角坐标为(1,1),右下角坐标为(2^n, 2^n)。该曲线在2^(n+1)*2^(n+1)上的正方形上的图案,可以由2^n * 2^n的情况构造出来。构造方法:左上角和右上角保持不变,左下角顺时针90度,右下角逆时针90度,然后各部分按照虚线相连即可。有n<30,x,y<2^30。输入n和p点坐标(x, y),答案输出曲线上该点覆盖的格子的序号。注:格子的序号是从(1,1)开始沿着曲线所覆盖的第几个格子。
代码:
#include
long long f(int n, int x, int y)
{
if(n == 0) return 1;
long long m = 1LL << (n-1);
if(x <= m && y <= m)
return f(n-1, y, x);
if(x > m && y <= m)
return 3LL * m * m + f(n-1, ,2*m-x+1); //填空
if(x <= m && y > m)
return 1LL * m * m + f(n-1, x, y-m);
if(x > m && y > m)
return 2LL * m * m + f(n-1, x-m, y-m);
}
int main()
{
int n, x, y;
scanf("%d %d %d", &n, &x, &y);
printf("%lld\n", f(n, x, y));
return 0;
} 参考答案:m-y+1
【解释】给出的代码是使用分治法,通过分析给出的4个if语句可以判断出依次是处理左下、右下、左上、右上,需要我们填空的部分是处理右下角的。分治法是将大问题变为相同性质的小问题,因此是要将右下角的图形逆时针90度。
假设正方形是m*m,那么顺时针90度,就是将第1行变为第1列,第2行变为第2列,……第m行变为第m列。而逆时针90度,就是将第1行变为第m列,第2行变为第m-1列,……,第m行变为第1列。右下角的部分需要纵坐标平移m个单位后,再逆时针90度。
顺时针90度:(x, y) ==> (y, x)
逆时针90度:(x, y) ==> (m-y+1, m-x+1)
第四题:找环
题意:
编号为1到n的n个点,以及n-1条边构成一棵树。现在在树上加上一条边,这样就构成了一个含环的图了。请你找出该环上的结点,从小到大输出这些结点编号。
测试数据:
30%数据:n<1000
100%数据:n<100000
输入样例:
5
1 2
2 5
4 2
1 3
5 3
输出样例:
1 2 3 5
【题解】
计算出每个点的度数。明显度数为1的点不可能在环上,那么与该点唯一相连的边也就不在环上了,可以删去。删去这条边后,这边的另一个端点度数减去1,如果因此而导致它的度数变为1了,同样说明该点不在环上,可以去掉,不断重复以上操作,直到没有边可以删去。
参考代码中用一个队列来维护边。由于点数n很大,无法使用邻接矩阵,只能使用邻接表来存储图,代码中使用vector容器来实现。
参考代码:
#include
#include
#include
#include
using namespace std;
#define maxn 100010
int d[maxn];
vector e[maxn];
typedef struct EDGE
{
int u, v;
EDGE(int a=0, int b=0):u(a),v(b){}
}Edge;
queue q;
int n;
void init()
{
memset(d, 0, sizeof(d));
scanf("%d", &n);
int a, b;
for(int i = 1; i <= n; i++)
{
scanf("%d %d", &a, &b);
d[a]++;
d[b]++;
e[a].push_back(b);
e[b].push_back(a);
q.push(Edge(a,b));
}
}
void out()
{
bool flag = false;
for(int i = 1; i <= n; i++)
if(d[i] > 0)
{
if(!flag){ printf("%d", i); flag = true; }
else
printf(" %d", i);
}
putchar('\n');
}
void solve()
{
while(!q.empty())
{
Edge tmp = q.front(); q.pop();
if(d[tmp.u] == 1 || d[tmp.v] == 1) //其中一个端点的度为1时,删去该边
{
d[tmp.u]--;
d[tmp.v]--;
int p;
if(d[tmp.u] == 1)
{
p = tmp.u;
int size = e[p].size();
for(int i = 0; i < size; i++)
{
int t = e[p][i];
if(d[t] > 0) q.push(Edge(p, t));
}
}
if(d[tmp.v] == 1)
{
p = tmp.u;
int size = e[p].size();
for(int i = 0; i < size; i++)
{
int t = e[p][i];
if(d[t] > 0) q.push(Edge(p, t));
}
}
}
}
}
int main()
{
init();
solve();
out();
return 0;
}
第五题:在线匹配
题意:
有n个人在线上玩游戏,每人的积分分别为Ai。如果线上的某两个人的积分恰好相差为k时,他们就会被进行匹配。问线上最多会有多少人,他们任意两人均没法进行匹配?
测试数据:
30%数据:n<10
100%数据:n<100000,Ai<100000,k<100000
输入样例1:
10 0
1 4 2 3 6 7 1 4 2 3
输出样例1:
6
输入样例2:
10 3
1 1 1 1 4 4 1 1 1 1
输出样例2:
8
【题解】
方法一:
30%数据n<10,所以可以用深度搜索,每个数只有选和不选,得到一组待定的数列后,再检查一下是否两两不能匹配,是则用当前数列的个数去尝试更新答案。时间复杂度是O(n*2^n)。
方法二:
将每个数值看作点,把可以匹配的两个数连一条边,那么问题转化为:删去最少的点,使得剩下的点中不存在相连的边。
对于每条边,明显两个端点只能选一个,按照贪心思想,易知应该优先去掉度数多的那个点。
算法步骤:
(1)构图,将积分恰好相差k的两个点相连;
(2)计算出所有点的度数;
(3)找出度数最大的那个点;
(4)把与该点相连的所有点的度数减去1,把该点的度数置为-1表示已经删去该点;
(5)重复(4)(5),直到没有边可以删去;
(6)这时剩余的点的度数均为0,统计出其个数,就是最大不能两两匹配的个数。
时间复杂度为O(n^2)
(n<100000,该方法仍然无法通过所有测试数据,希望有大神能够提供更优秀的方法)
参考代码:
#include
#include
#include
using namespace std;
#define maxn 100010
vector e[maxn];
int a[maxn]; //a[i]表示第i个人的积分
int d[maxn]; //d[i]表示第i个点的度数
bool exist[maxn]; //exist[i]=false表示第i个点删去
int n, k;
void init()
{
scanf("%d %d", &n, &k);
for(int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
}
void out()
{
int ans = 0;
for(int i = 1; i <= n; i++)
if(exist[i]) ans++;
printf("%d\n", ans);
}
void solve()
{
memset(d, 0, sizeof(d));
int i, j;
for(i = 1; i < n; i++)
for(j = i+1; j <= n; j++)
{
if(a[i] - a[j] == k || a[j] - a[i] == k)
{
e[i].push_back(j);
e[j].push_back(i);
d[i]++;
d[j]++;
}
}
memset(exist, true, sizeof(exist));
do{
int maxv = 0, sign = -1;
int i;
for(i = 1; i <= n; i++)
if(exist[i])
{
if(d[i] > maxv) maxv = d[sign = i];
}
if(maxv == 0)
break;
else{
int size = e[sign].size();
for(i = 0; i < size; i++)
{
int p = e[sign][i];
if(exist[p]) d[p]--;
}
exist[sign] = false;
d[sign] = -1;
}
}while(1);
}
int main()
{
init();
solve();
out();
return 0;
} 第六题:观光铁路
跳蚤国正在大力发展旅游业,每个城市都被打造成了旅游景点。
许多跳蚤想去其他城市旅游,但是由于跳得比较慢,它们的愿望难以实现。这时,小C听说有一种叫做火车的交通工具,在铁路上跑得很快,便抓住了商机,创立了一家铁路公司,向跳蚤国王请示在每两个城市之间都修建铁路。
然而,由于小C不会扳道岔,火车到一个城市以后只能保证不原路返回,而会随机等概率地驶向与这个城市有铁路连接的另外一个城市。
跳蚤国王向广大居民征求意见,结果跳蚤们不太满意,因为这样修建铁路以后有可能只游览了3个城市(含出发的城市)以后就回来了,它们希望能多游览几个城市。于是跳蚤国王要求小C提供一个方案,使得每只跳蚤坐上火车后能多游览几个城市才回来。
小C提供了一种方案给跳蚤国王。跳蚤国王想知道这个方案中每个城市的居民旅游的期望时间(设火车经过每段铁路的时间都为1),请你来帮跳蚤国王。
【输入格式】
输入的第一行包含两个正整数n、m,其中n表示城市的数量,m表示方案中的铁路条数。
接下来m行,每行包含两个正整数u、v,表示方案中城市u和城市v之间有一条铁路。
保证方案中无重边无自环,每两个城市之间都能经过铁路直接或间接到达,且火车由任意一条铁路到任意一个城市以后一定有路可走。
【输出格式】
输出n行,第i行包含一个实数ti,表示方案中城市i的居民旅游的期望时间。你应当输出足够多的小数位数,以保证输出的值和真实值之间的绝对或相对误差不超过1e-9。
【样例输入】
4 5
1 2
2 3
3 4
4 1
1 3
【样例输出】
3.333333333333
5.000000000000
3.333333333333
5.000000000000
【样例输入】
10 15
1 2
1 9
1 5
2 3
2 7
3 4
3 10
4 5
4 8
5 6
6 7
6 10
7 8
8 9
9 10
【样例输出】
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
10.000000000000
【数据规模与约定】
对于10%的测试点,n <= 10;
对于20%的测试点,n <= 12;
对于50%的测试点,n <= 16;
对于70%的测试点,n <= 19;
对于100%的测试点,4 <= k <= n <= 21,1 <= u, v <= n。数据有梯度。
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms
【题解】
这题我也没有什么思路,还没想到什么解决方法。