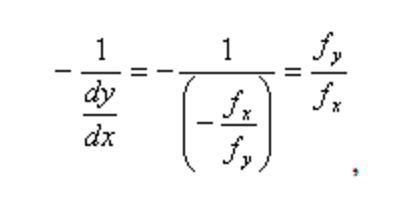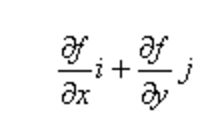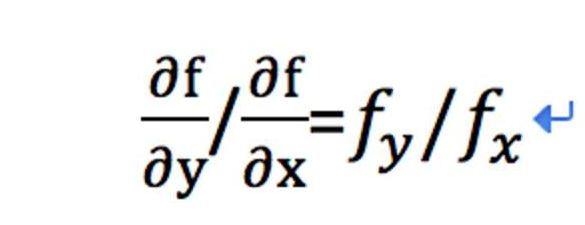- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- OC语言多界面传值五大方式
Magnetic_h
iosui学习objective-c开发语言
前言在完成暑假仿写项目时,遇到了许多需要用到多界面传值的地方,这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值,简单地说就是通过访问后一个视图控制器的属性来为它赋值,通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
- 理解Gunicorn:Python WSGI服务器的基石
范范0825
ipythonlinux运维
理解Gunicorn:PythonWSGI服务器的基石介绍Gunicorn,全称GreenUnicorn,是一个为PythonWSGI(WebServerGatewayInterface)应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具,Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置,帮助初学者快速上手。1.什么是Gunico
- ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
- Python数据分析与可视化实战指南
William数据分析
pythonpython数据
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前,我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
- git常用命令笔记
咩酱-小羊
git笔记
###用习惯了idea总是不记得git的一些常见命令,需要用到的时候总是担心旁边站了人~~~记个笔记@_@,告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"
[email protected]"基本操作克隆远程仓库gitclone查看
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- Git常用命令-修改远程仓库地址
猿大师
LinuxJavagitjava
查看远程仓库地址gitremote-v返回结果originhttps://git.coding.net/*****.git(fetch)originhttps://git.coding.net/*****.git(push)修改远程仓库地址gitremoteset-urloriginhttps://git.coding.net/*****.git先删除后增加远程仓库地址gitremotermori
- Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- mac电脑命令行获取电量
小米人er
我的博客macos命令行
在macOS上,有几个命令行工具可以用来获取电量信息,最常用的是pmset命令。你可以通过以下方式来查看电池状态和电量信息:查看电池状态:pmset-gbatt这个命令会返回类似下面的输出:Nowdrawingfrom'BatteryPower'-InternalBattery-0(id=1234567)95%;discharging;4:02remainingpresent:true输出中包括电
- 数字里的世界17期:2021年全球10大顶级数据中心,中国移动榜首
张三叨
你知道吗?2016年,全球的数据中心共计用电4160亿千瓦时,比整个英国的发电量还多40%!前言每天,我们都会创造超过250万TB的数据。并且随着物联网(IOT)的不断普及,这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代,但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术,比如人工智能和机器学习,已经将我们推向
- nosql数据库技术与应用知识点
皆过客,揽星河
NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- Shell、Bash、Zsh这都是啥啊
小白码上飞
bashlinux开发语言
Zsh和Bash都是我们常用的Shell,那先搞明白啥是shell吧。Shell作为一个单词,他是“壳”的意思,蛋壳坚果壳。之所以叫壳,是为了和计算机的“核”来区分,用它表示“为使用者提供的操作界面”。所以这个命名其实很形象,翻译成中文,直译过来叫“壳层”。个人认为这个叫法很奇怪,意译貌似也没有什么好的词汇来匹配。就还是叫shell吧。维基百科给的定义是:Incomputing,ashellisa
- 一文掌握python常用的list(列表)操作
程序员neil
pythonpython开发语言
目录一、创建列表1.直接创建列表:2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素,索引从0开始:2.还可以使用切片操作访问列表的一部分:三、修改列表元素四、添加元素1.append():在末尾添加元素2.insert():在指定位置插入元素五、删除元素1.del:删除指定位置的元素2.remove():删除指定值的第一个匹配项3.pop():
- 发现荞麦过敏这件事
怪小泊
荞麦在我这里不是常用的谷物。所以前二十年,我以为自己是很正常的,从街头小吃到包装零食到每日三餐,从来没有不能吃的。可是有天我突然病倒了,喉咙火辣辣的肿痛,口水都咽不下去,舌头发麻。当时我以为吃太多零食所致,因为那天我吃了很辣的泡椒凤爪。其实我是不怎么吃辣的。而那个泡椒凤爪真的超辣。当时我以为自己吃多了,并不知道自己对哪个食物过敏。因为不舒服我早早睡了,结果并没有睡着。肚子一阵一阵疼,非常痛苦,终于
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- Linux vi常用命令
fengyehongWorld
Linuxlinux
参考资料viコマンド(vimコマンド)リファレンス目录一.保存系命令二.删除系命令三.移动系命令四.复制粘贴系命令一.保存系命令⏹保存并退出:wq⏹强制保存并退出:wq!⏹退出(文件未编辑):q⏹强制退出(忽略已编辑内容):q!⏹另存为:w新文件名二.删除系命令⏹删除当前行dd⏹清空整个文档gg:移动到文档顶部dG:删除到最后一行ggdG三.移动系命令⏹移动到文档顶部gg⏹移动到文档底部#方式1G
- 语文主题教学学习笔记之87
东哥杂谈
“语文主题教学”学习笔记之八十七(0125)今天继续学习小学语文主题教学的实践样态。板块三:教学中体现“书艺”味道。作为四大名著之一的《水浒传》,堪称我国文学宝库之经典。对从《水浒传》中摘选的单元,教师就要了解其原生态,即评书体特点。这也要求教师要了解一些常用的评书行话术语,然后在教学时适时地加入一些,让学生体味其文本中原有的特色。学生也要尽可能地通过朗读的方式,而不单是分析讲解的方式进行学习。细
- Linux查看服务器日志
TPBoreas
运维linux运维
一、tail这个是我最常用的一种查看方式用法如下:tail-n10test.log查询日志尾部最后10行的日志;tail-n+10test.log查询10行之后的所有日志;tail-fn10test.log循环实时查看最后1000行记录(最常用的)一般还会配合着grep用,(实时抓包)例如:tail-fn1000test.log|grep'关键字'(动态抓包)tail-fn1000test.log
- MongoDB知识概括
GeorgeLin98
持久层mongodb
MongoDB知识概括MongoDB相关概念单机部署基本常用命令索引-IndexSpirngDataMongoDB集成副本集分片集群安全认证MongoDB相关概念业务应用场景:传统的关系型数据库(如MySQL),在数据操作的“三高”需求以及应对Web2.0的网站需求面前,显得力不从心。解释:“三高”需求:①Highperformance-对数据库高并发读写的需求。②HugeStorage-对海量数
- mac 备份android 手机通讯录导入iphone,iphone如何导出通讯录(轻松教你iPhone备份通讯录的方法)...
weixin_39762838
mac备份android手机通讯录导入iphone
在日新月异的手机更替中,换手机已经成为一个非常稀松平常的事情,但将旧手机上面的通讯录导入到新手机还是让不少小伙伴为难,本篇将给大家详细讲解这方面的知识:“苹果手机通讯录怎么导入到新手机”及“安卓手机通讯录导入到新手机”的方法。一、苹果手机通讯录导入到新手机常用方法(SIM卡导入)在苹果手机主频幕上找到“设置”,单击进入设置菜单,下拉菜单列表,点击“邮件、通讯录、日历”,然后找到“导入SIM卡通讯录
- 利用python实现图片格式之间的相互转换
难得北窗高卧
python开发语言
一、概要图片一般有多种格式,常见的图片格式包括:JPEG(.jpg或.jpeg):一种广泛使用的有损压缩格式,适用于摄影图像和网页上的图片。PNG(.png):一种无损压缩格式,支持透明度和更好的图像质量,常用于图标、图形和需要透明背景的图片。该图片是4通道的,外加一个透明通道。如截屏GIF(.gif):一种支持动画和透明度的格式,常用于简单的动画和图标。BMP(.bmp):一种无损格式,存储图像
- 遥感影像的切片处理
sand&wich
计算机视觉python图像处理
在遥感影像分析中,经常需要将大尺寸的影像切分成小片段,以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务,如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程,同时确保每个影像片段保留正确的地理信息。准备环境首先,确保安装了必要的Python库,包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
- 入门MySQL——查询语法练习
K_un
前言:前面几篇文章为大家介绍了DML以及DDL语句的使用方法,本篇文章将主要讲述常用的查询语法。其实MySQL官网给出了多个示例数据库供大家实用查询,下面我们以最常用的员工示例数据库为准,详细介绍各自常用的查询语法。1.员工示例数据库导入官方文档员工示例数据库介绍及下载链接:https://dev.mysql.com/doc/employee/en/employees-installation.h
- 更改npm镜像源为淘宝镜像
骆小骆
基于node.js
npm常用指令后缀*最近复习了一下node.js整理了一下跟node.js相关的指令后缀*--save、-S参数意思是把模块的版本信息保存到dependencies(生产环境依赖)中,即你的package.json文件的dependencies字段中;–--save-dev、-D参数意思是把模块版本信息保存到devDependencies(开发环境依赖)中,即你的package.json文件的de
- 常见的 JVM 调优方法有哪些?
爪哇天下
jvm
常见的JVM调优方法有哪些?可以具体到调整哪个参数,调成什么值?对年轻代的EdenSurvivor的比例进行配置-XX:SurvivorRatio=8:表示设置2个Survivor区:1个Eden区的大小比值为2:8,这意味着Survivor区占整个年轻代的1/5,这个参数默认为8如果经常性的SurvivorTo放不下YGC的剩余的对象时候,可以适当的调整比例常用的CMS收集器:设置回收阈值,需要
- 补充元象二面
Redstone Monstrosity
前端面试
1.请尽可能详细地说明,防抖和节流的区别,应用场景?你的回答中不要写出示例代码。防抖(Debounce)和节流(Throttle)是两种常用的前端性能优化技术,它们的主要区别在于如何处理高频事件的触发。以下是防抖和节流的区别和应用场景的详细说明:防抖和节流的定义防抖:在一段时间内,多次执行变为只执行最后一次。防抖的原理是,当事件被触发后,设置一个延迟定时器。如果在这个延迟时间内事件再次被触发,则重
- pyhon+ffmpeg 常用音视频处理命令
不再游移
ffmpeg音视频python
FFmpeg是多媒体领域的万能工具。只要涉及音视频领域的处理,基本上没有它做不了的事情!通俗点讲,从视频录制、视频编辑再到播放,它都能做!前段时间做了个短视频自动化脚本项目,需要自动处理音视频(包括一些合成、拼接、转场、调色等等),当时做的时候找各种命令还是很痛苦的,因此对用到的所有处理命令做了个汇总,方便以后使用。目录一、获取音频时长二、获取视频信息三、获取视频时长四、多个视频合并五、视频提取视
- 对股票分析时要注意哪些主要因素?
会飞的奇葩猪
股票 分析 云掌股吧
众所周知,对散户投资者来说,股票技术分析是应战股市的核心武器,想学好股票的技术分析一定要知道哪些是重点学习的,其实非常简单,我们只要记住三个要素:成交量、价格趋势、振荡指标。
一、成交量
大盘的成交量状态。成交量大说明市场的获利机会较多,成交量小说明市场的获利机会较少。当沪市的成交量超过150亿时是强市市场状态,运用技术找综合买点较准;
- 【Scala十八】视图界定与上下文界定
bit1129
scala
Context Bound,上下文界定,是Scala为隐式参数引入的一种语法糖,使得隐式转换的编码更加简洁。
隐式参数
首先引入一个泛型函数max,用于取a和b的最大值
def max[T](a: T, b: T) = {
if (a > b) a else b
}
因为T是未知类型,只有运行时才会代入真正的类型,因此调用a >
- C语言的分支——Object-C程序设计阅读有感
darkblue086
applec框架cocoa
自从1972年贝尔实验室Dennis Ritchie开发了C语言,C语言已经有了很多版本和实现,从Borland到microsoft还是GNU、Apple都提供了不同时代的多种选择,我们知道C语言是基于Thompson开发的B语言的,Object-C是以SmallTalk-80为基础的。和C++不同的是,Object C并不是C的超集,因为有很多特性与C是不同的。
Object-C程序设计这本书
- 去除浏览器对表单值的记忆
周凡杨
html记忆autocompleteform浏览
&n
- java的树形通讯录
g21121
java
最近用到企业通讯录,虽然以前也开发过,但是用的是jsf,拼成的树形,及其笨重和难维护。后来就想到直接生成json格式字符串,页面上也好展现。
// 首先取出每个部门的联系人
for (int i = 0; i < depList.size(); i++) {
List<Contacts> list = getContactList(depList.get(i
- Nginx安装部署
510888780
nginxlinux
Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器,也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的,第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证的形式发布,因它的稳定性、丰富的功能集、示例配置文件和低系统资源
- java servelet异步处理请求
墙头上一根草
java异步返回servlet
servlet3.0以后支持异步处理请求,具体是使用AsyncContext ,包装httpservletRequest以及httpservletResponse具有异步的功能,
final AsyncContext ac = request.startAsync(request, response);
ac.s
- 我的spring学习笔记8-Spring中Bean的实例化
aijuans
Spring 3
在Spring中要实例化一个Bean有几种方法:
1、最常用的(普通方法)
<bean id="myBean" class="www.6e6.org.MyBean" />
使用这样方法,按Spring就会使用Bean的默认构造方法,也就是把没有参数的构造方法来建立Bean实例。
(有构造方法的下个文细说)
2、还
- 为Mysql创建最优的索引
annan211
mysql索引
索引对于良好的性能非常关键,尤其是当数据规模越来越大的时候,索引的对性能的影响越发重要。
索引经常会被误解甚至忽略,而且经常被糟糕的设计。
索引优化应该是对查询性能优化最有效的手段了,索引能够轻易将查询性能提高几个数量级,最优的索引会比
较好的索引性能要好2个数量级。
1 索引的类型
(1) B-Tree
不出意外,这里提到的索引都是指 B-
- 日期函数
百合不是茶
oraclesql日期函数查询
ORACLE日期时间函数大全
TO_DATE格式(以时间:2007-11-02 13:45:25为例)
Year:
yy two digits 两位年 显示值:07
yyy three digits 三位年 显示值:007
- 线程优先级
bijian1013
javathread多线程java多线程
多线程运行时需要定义线程运行的先后顺序。
线程优先级是用数字表示,数字越大线程优先级越高,取值在1到10,默认优先级为5。
实例:
package com.bijian.study;
/**
* 因为在代码段当中把线程B的优先级设置高于线程A,所以运行结果先执行线程B的run()方法后再执行线程A的run()方法
* 但在实际中,JAVA的优先级不准,强烈不建议用此方法来控制执
- 适配器模式和代理模式的区别
bijian1013
java设计模式
一.简介 适配器模式:适配器模式(英语:adapter pattern)有时候也称包装样式或者包装。将一个类的接口转接成用户所期待的。一个适配使得因接口不兼容而不能在一起工作的类工作在一起,做法是将类别自己的接口包裹在一个已存在的类中。 &nbs
- 【持久化框架MyBatis3三】MyBatis3 SQL映射配置文件
bit1129
Mybatis3
SQL映射配置文件一方面类似于Hibernate的映射配置文件,通过定义实体与关系表的列之间的对应关系。另一方面使用<select>,<insert>,<delete>,<update>元素定义增删改查的SQL语句,
这些元素包含三方面内容
1. 要执行的SQL语句
2. SQL语句的入参,比如查询条件
3. SQL语句的返回结果
- oracle大数据表复制备份个人经验
bitcarter
oracle大表备份大表数据复制
前提:
数据库仓库A(就拿oracle11g为例)中有两个用户user1和user2,现在有user1中有表ldm_table1,且表ldm_table1有数据5千万以上,ldm_table1中的数据是从其他库B(数据源)中抽取过来的,前期业务理解不够或者需求有变,数据有变动需要重新从B中抽取数据到A库表ldm_table1中。
- HTTP加速器varnish安装小记
ronin47
http varnish 加速
上午共享的那个varnish安装手册,个人看了下,有点不知所云,好吧~看来还是先安装玩玩!
苦逼公司服务器没法连外网,不能用什么wget或yum命令直接下载安装,每每看到别人博客贴出的在线安装代码时,总有一股羡慕嫉妒“恨”冒了出来。。。好吧,既然没法上外网,那只能麻烦点通过下载源码来编译安装了!
Varnish 3.0.4下载地址: http://repo.varnish-cache.org/
- java-73-输入一个字符串,输出该字符串中对称的子字符串的最大长度
bylijinnan
java
public class LongestSymmtricalLength {
/*
* Q75题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
* 比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
*/
public static void main(String[] args) {
Str
- 学习编程的一点感想
Cb123456
编程感想Gis
写点感想,总结一些,也顺便激励一些自己.现在就是复习阶段,也做做项目.
本专业是GIS专业,当初觉得本专业太水,靠这个会活不下去的,所以就报了培训班。学习的时候,进入状态很慢,而且当初进去的时候,已经上到Java高级阶段了,所以.....,呵呵,之后有点感觉了,不过,还是不好好写代码,还眼高手低的,有
- [能源与安全]美国与中国
comsci
能源
现在有一个局面:地球上的石油只剩下N桶,这些油只够让中国和美国这两个国家中的一个顺利过渡到宇宙时代,但是如果这两个国家为争夺这些石油而发生战争,其结果是两个国家都无法平稳过渡到宇宙时代。。。。而且在战争中,剩下的石油也会被快速消耗在战争中,结果是两败俱伤。。。
在这个大
- SEMI-JOIN执行计划突然变成HASH JOIN了 的原因分析
cwqcwqmax9
oracle
甲说:
A B两个表总数据量都很大,在百万以上。
idx1 idx2字段表示是索引字段
A B 两表上都有
col1字段表示普通字段
select xxx from A
where A.idx1 between mmm and nnn
and exists (select 1 from B where B.idx2 =
- SpringMVC-ajax返回值乱码解决方案
dashuaifu
AjaxspringMVCresponse中文乱码
SpringMVC-ajax返回值乱码解决方案
一:(自己总结,测试过可行)
ajax返回如果含有中文汉字,则使用:(如下例:)
@RequestMapping(value="/xxx.do") public @ResponseBody void getPunishReasonB
- Linux系统中查看日志的常用命令
dcj3sjt126com
OS
因为在日常的工作中,出问题的时候查看日志是每个管理员的习惯,作为初学者,为了以后的需要,我今天将下面这些查看命令共享给各位
cat
tail -f
日 志 文 件 说 明
/var/log/message 系统启动后的信息和错误日志,是Red Hat Linux中最常用的日志之一
/var/log/secure 与安全相关的日志信息
/var/log/maillog 与邮件相关的日志信
- [应用结构]应用
dcj3sjt126com
PHPyii2
应用主体
应用主体是管理 Yii 应用系统整体结构和生命周期的对象。 每个Yii应用系统只能包含一个应用主体,应用主体在 入口脚本中创建并能通过表达式 \Yii::$app 全局范围内访问。
补充: 当我们说"一个应用",它可能是一个应用主体对象,也可能是一个应用系统,是根据上下文来决定[译:中文为避免歧义,Application翻译为应
- assertThat用法
eksliang
JUnitassertThat
junit4.0 assertThat用法
一般匹配符1、assertThat( testedNumber, allOf( greaterThan(8), lessThan(16) ) );
注释: allOf匹配符表明如果接下来的所有条件必须都成立测试才通过,相当于“与”(&&)
2、assertThat( testedNumber, anyOf( g
- android点滴2
gundumw100
应用服务器android网络应用OSHTC
如何让Drawable绕着中心旋转?
Animation a = new RotateAnimation(0.0f, 360.0f,
Animation.RELATIVE_TO_SELF, 0.5f, Animation.RELATIVE_TO_SELF,0.5f);
a.setRepeatCount(-1);
a.setDuration(1000);
如何控制Andro
- 超简洁的CSS下拉菜单
ini
htmlWeb工作html5css
效果体验:http://hovertree.com/texiao/css/3.htmHTML文件:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>简洁的HTML+CSS下拉菜单-HoverTree</title>
- kafka consumer防止数据丢失
kane_xie
kafkaoffset commit
kafka最初是被LinkedIn设计用来处理log的分布式消息系统,因此它的着眼点不在数据的安全性(log偶尔丢几条无所谓),换句话说kafka并不能完全保证数据不丢失。
尽管kafka官网声称能够保证at-least-once,但如果consumer进程数小于partition_num,这个结论不一定成立。
考虑这样一个case,partiton_num=2
- @Repository、@Service、@Controller 和 @Component
mhtbbx
DAOspringbeanprototype
@Repository、@Service、@Controller 和 @Component 将类标识为Bean
Spring 自 2.0 版本开始,陆续引入了一些注解用于简化 Spring 的开发。@Repository注解便属于最先引入的一批,它用于将数据访问层 (DAO 层 ) 的类标识为 Spring Bean。具体只需将该注解标注在 DAO类上即可。同时,为了让 Spring 能够扫描类
- java 多线程高并发读写控制 误区
qifeifei
java thread
先看一下下面的错误代码,对写加了synchronized控制,保证了写的安全,但是问题在哪里呢?
public class testTh7 {
private String data;
public String read(){
System.out.println(Thread.currentThread().getName() + "read data "
- mongodb replica set(副本集)设置步骤
tcrct
javamongodb
网上已经有一大堆的设置步骤的了,根据我遇到的问题,整理一下,如下:
首先先去下载一个mongodb最新版,目前最新版应该是2.6
cd /usr/local/bin
wget http://fastdl.mongodb.org/linux/mongodb-linux-x86_64-2.6.0.tgz
tar -zxvf mongodb-linux-x86_64-2.6.0.t
- rust学习笔记
wudixiaotie
学习笔记
1.rust里绑定变量是let,默认绑定了的变量是不可更改的,所以如果想让变量可变就要加上mut。
let x = 1; let mut y = 2;
2.match 相当于erlang中的case,但是case的每一项后都是分号,但是rust的match却是逗号。
3.match 的每一项最后都要加逗号,但是最后一项不加也不会报错,所有结尾加逗号的用法都是类似。
4.每个语句结尾都要加分