光子噪声

学习了光子噪声的一些知识，因此记录一下，如有错误希望大家指正

原理

光子噪声是由于到达传感器的光子数目发生变化，导致实际情况与理论情况发生偏差而产生的噪声。
光是由离散的粒子构成的（光的粒子性），一个粒子在一幅图像中出现的位置是不确定的，通常用概率来描述，而光子撒下位置的概率分布就是光强分布，对一幅图像来说，光子落在某处的概率为这个像素的能量除以总能量。

泊松分布

二项分布和泊松分布

二项分布: 对于一个事件，在一次实验中发生的概率为p,未发生的概率为（1-p）,重复n次，因此可能发生的次数X取值为k（0,1，…n）的概率为：

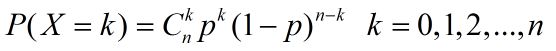
泊松分布：若随机变量X的取值为0,1,2…，n，且概率分布为：

则称X服从泊松分布，其中$\lambda$大于0。对于所有的k进行求和，即${\sum }_{k}P(X=k)=1$,因此可得:
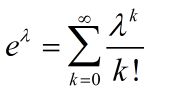两者关系:令$\lambda =np$,泊松分布是二项分布的极限分布，证明如下：

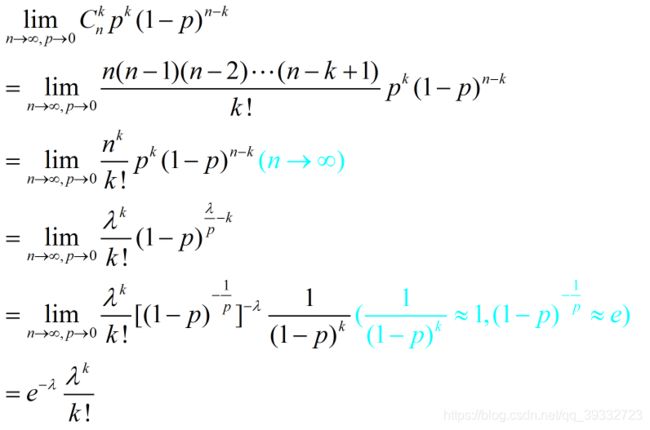
从上述推导可以看出（颜色标记的为近似）可以看出，当二项分布中的试验次数n足够大，时间A在一次事件中发生的概率p足够小，则二项分布近似为泊松分布。

对一个像素点来说，能否接收到光子可以用二项分布来进行描述，该像素点对于整个平面来说，接收到的概率较小，但是整个平面接收到的光子数目较多（相当于进行很多次实验），因此近似为泊松分布，因此光子噪声又称为泊松噪声。且由于均值和方差相同，因此，当光子数目增多时，均值增大，方差增大，噪声（一般用标准差表示噪声）增大。可以理解为光子数目多了，出现错误的可能性也就大了。

实验

1.对图像加光子噪声，MATLAB有自带的加噪函数imnoise():

I = rgb2gray(imread('data/lena256.bmp'));
figure,subplot(1,2,1),imshow(uint8(I)),title('original image')
g=imnoise(I,'poisson');
subplot(1,2,2),imshow(uint8(g)),title('poisson noise');

输出结果如下所示：

泊松噪声与图像的灰度值有关，因此可以从图像中明显看出来。
注意：在MATLAB中用imnoise()添加泊松噪声时，对不同的数据类型具有不同的操作：
double：用$e12$进行缩放。例如，一个像素值为$5.5e-12$,先乘以$e12$,则对应的输出像素用均值为5.5的泊松分布生成，之后除以$e12$得到真实的像素值。
single：缩放的比例因子为$e6$
uint8/uint16：不进行缩放，例如，一个像素值为10，则对应的输出像素用均值为10的泊松分布生成。
对一幅图像来说，数据如果是double类型，由于$e12$值很大，因此会导致添加泊松噪声后变化不明显，如下所示：

 I= im2double(rgb2gray(imread('data/lena256.bmp')));
figure,subplot(1,2,1),imshow(I),title('original image')
g=imnoise(I,'poisson');
subplot(1,2,2),imshow(g),title('poisson noise');

2.模拟传感器接收到的图像，将光子按照一定概率撒在不同的位置，光子落在某处的概率为这个像素的能量除以总能量。用MATLAB自带的函数randsrc()，是指按照一定概率生成伪随机矩阵。

N = length(I(:));%代表像素位置
P = I/sum(I(:));%概率
photonNum=1000000;%光子数目
b = randsrc(photonNum, 1, [1:N;P(:).']);%对于任意一个光子，按照一定概率随机落到一个像素点位置
Iphoton = hist(b, N);
Iphoton = reshape(Iphoton, size(I));

可以看出，光子数目越多，图像内容越明显。

参考内容

[1].一篇文章看懂散粒噪声
[2].散粒噪声 shot noise 泊松噪声
[3].二项分布和泊松分布，二者的关系