归并排序
算法原理
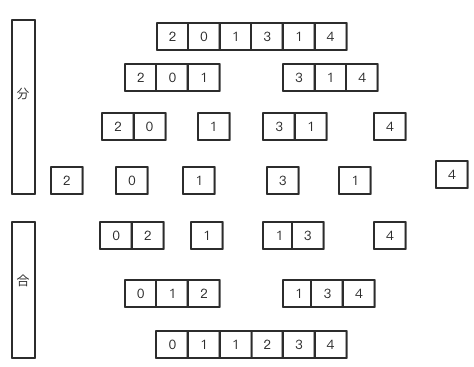
归并排序是一种经典的排序算法(分分合合)
- 分: 递归的将元素数组进行拆分,1分2,2分4...
-
合: 当子数组拆分为只有一个元素时,递归的合并子数组并排序
算法实现
public class Merge {
//i,j分别指向待合并的两个子数组的尾部,两者指向的元素相比较,小的那个被copy进输出数组中,并且指针向前移动一个
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++]; //指针前移
else a[k] = aux[i++]; //指针前移
}
}
//递归拆分 而后合并
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid + 1, hi);
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) {
aux = new Comparable[a.length];
sort(a, aux, 0, a.length - 1);
}
}
算法复杂度分析
根据上面的图示可以看出分合都产生了二叉树型的结构,我们由此可知它在比较上的时间花费大约lgN,在数组访问上的时间花费大约6lgN。
空间复杂度:在merge的时候对被merge数组进行了全量的copy
算法优化
- 当子数组长度较小时,改用插入排序(我不晓得这样做好在哪里)
- 当子数组已经有序时,不进行merge:
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
{
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort (a, aux, lo, mid);
sort (a, aux, mid+1, hi);
//由于被merge的两个子数组都已经时有序的,所以可以这样进行比较
if (!less(a[mid+1], a[mid])) return;
merge(a, aux, lo, mid, hi);
}
3.通过变换a与aux的位置来,省去每次merge时对aux的copy
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi)
{
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
{
if (i > mid) aux[k] = a[j++];
else if (j > hi) aux[k] = a[i++];
else if (less(a[j], a[i])) aux[k] = a[j++];
else aux[k] = a[i++];
}
}
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi)
{
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort (aux, a, lo, mid);
sort (aux, a, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
变种:不需要递归的归并排序
public class MergeBU
{
public static void sort(Comparable[] a)
{
int N = a.length;
Comparable[] aux = new Comparable[N];
//第一个循环控制间隔
for (int sz = 1; sz < N; sz = sz+sz)
//第二个循环进行merge
for (int lo = 0; lo < N-sz; lo += sz+sz)
merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
}
}
关于排序算法复杂度的探讨
排序算法的过程可以使用决策树来表示:
而N个元素的排序结果最多又N!种,即N!个叶子节点,所以层高为lgN!,即约等于NlgN。 所以任何排序算法,在最糟糕的情况下, 需要的算法复杂度至少为NlgN。
稳定性
对于相同的元素,在排序后仍旧保持排序前的相对顺序,我们称这种算法是稳定的。
- 具有稳定性的算法有:插入排序,归并排序
- 不稳定的算法:选择排序,希尔排序