matlab学习：人脸识别之LBP (Local Binary Pattern)

1.算法简介

　　LBP是一种简单，有效的纹理分类的特征提取算法。LBP算子是由Ojala等人于1996年提出的，主要的论文是"Multiresolution gray-scale and rotation invariant texture classification with local binary patterns", pami, vol 24, no.7, July 2002。LBP就是"local binary pattern"的缩写。

　　关于论文的讲解可参考链接　　http://blog.sina.com.cn/s/blog_916b71bb0100w043.html

　　从纹理分析的角度来看，图像上某个像素点的纹理特征，大多数情况下是指这个点和周围像素点的关系，即这个点和它的邻域内点的关系。从哪个角度对这种关系提取特征，就形成了不同种类的特征。有了特征，就能根据纹理进行分类。LBP构造了一种衡量一个像素点和它周围像素点的关系。　

 

 

　　对图像中的每个像素，通过计算以其为中心的3*3邻域内各像素和中心像素的大小关系，把像素的灰度值转化为一个八位二进制序列。具体计算过程如下图所示，对于图像的任意一点Ic，其LBP特征计算为，以Ic为中心，取与Ic相邻的8各点，按照顺时针的方向记为 I0,I1,...,I7；以Ic点的像素值为阈值，如果 Ii 点的像素值小于Ic，则 Ii 被二值化为0，否则为1；将二值化得到的0、1序列看成一个8位二进制数，将该二进制数转化为十进制就可得到Ic点处的LBP算子的值。
　　基本的LBP算子只局限在3*3的邻域内，对于较大图像大尺度的结构不能很好的提取需要的纹理特征，因此研究者们对LBP算子进行了扩展。新的LBP算子LBP（P,R） 可以计算不同半径邻域大小和不同像素点数的特征值，其中P表示周围像素点个数，R表示邻域半径，同时把原来的方形邻域扩展到了圆形，下图给出了四种扩展后的LBP例子，其中，R可以是小数，对于没有落到整数位置的点，根据轨道内离其最近的两个整数位置像素灰度值，利用双线性差值的方法可以计算它的灰度值。

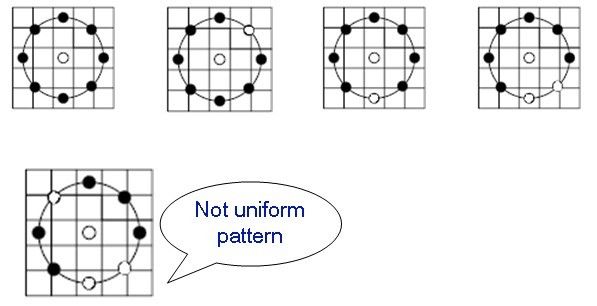
　　LBP(P,R)有2^p个值，也就是说图像共有2^p种二进制模型，然而实际研究中发现，所有模式表达信息的重要程度是不同的，统计研究表明，一幅图像中少数模式特别集中，达到总模式的百分之九十左右的比例，Ojala等人定义这种模式为Uniform模式，如果一个二进制序列看成一个圈时，0-1以及1-0的变化出现的次数总和不超过两次，那么这个序列就是Uniform模式 ，比如，00000000、00011110、00100001、11111111，在使用LBP表达图像纹理时，通常只关心Uniform模式，而将所有其他的模式归到同一类中。

人脸图像的各种LBP模式如下图所示，由图中可以看出，变化后的图像和原图像相比，能更清晰的体现各典型区域的纹理，同时又淡化了对于研究价值不大的平滑区域的特征，同时降低了特征的维数。比较而言，Uniform模式表现的更逼真，在人脸识别和表情识别应用中，都是采用这种模式。

 

　　在表情识别中，最常用的是把LBP的统计柱状图作为表情图像的特征向量。为了考虑特征的位置信息，把图像分成若干个小区域，在每个小区域里进行直方图统计，即统计该区域内属于某一模式的数量，最后再把所有区域的直方图一次连接到一起作为特征向量接受下一级的处理。

　　LBP算子利用了周围点与该点的关系对该点进行量化。量化后可以更有效地消除光照对图像的影响。只要光照的变化不足以改变两个点像素值之间的大小关系，那么LBP算子的值不会发生变化，所以一定程度上，基于LBP的识别算法解决了光照变化的问题，但是当图像光照变化不均匀时，各像素间的大小关系被破坏，对应的LBP模式也就发生了变化。

　　如果图像旋转了，那么纹理特征就旋转了，这时得到的2进制串也就旋转了，LBP值会相应变化。为了让LBP具有旋转不变性，将二进制串进行旋转。假设一开始得到的LBP特征为10010000，那么将这个二进制特征，按照顺时针方向旋转，可以转化为00001001的形式，这样得到的LBP值是最小的。无论图像怎么旋转，对点提取的二进制特征的最小值是不变的，用最小值作为提取的LBP特征，这样LBP就是旋转不变的了。当P=8时，能产生的不同的二进制特征数量是2^8个，经过上述表示，就变为36个。(我以为应当是2^8/8=32个)